结构重参数化之二：RepVGG

论文 RepVGG: Making VGG-style ConvNets Great Again

代码 GitHub - DingXiaoH/RepVGG: RepVGG: Making VGG-style ConvNets Great Again

前言

        相比于VGG这种简单重复堆叠conv、ReLU、pooling层的plain结构，Inception、ResNet、DenseNet等引入了更复杂的结构并带来了精度的提升，但这些复杂的结构也有缺点

1. 复杂的多分支结构（例如ResNet中的残差和Inception中的分支连接结构）使得模型难以实现和定制，降低了推理速度和内存利用率。
2. 一些组件（例如Xception和MobileNets中的深度可分离卷积、ShuffleNets中的channel shuffle）增加了内存访问成本，并且缺乏对各种设备的支持。

        影响模型推理速度的因素有很多，浮点运算（FLOPs）并不能准确地反映实际速度。尽管一些新模型的FLOPs比旧模型例如VGG、ResNet等的低，但实际推理速度可能并没有更快。 

        VGG这种plain结构的精度很难达到多分支结构的水平，其中一个原因是：多分支结构使得模型成为多个小模型的隐式集和，从而可以避免梯度消失问题。

        本文作者提出了RepVGG，一种新的模型架构，训练时是一种多分支结构，可以带来更高的精度，推理时通过结构重参数化技术等价转化成单分支结构，在保持精度不变的同时又能带来更快的推理速度。

介绍

Simple is Fast, Memory-economical, Flexible

        Fast  许多多分支模型的FLOPs比VGG低，但速度并没有更快。例如，VGG-16的FLOPs是EfficientNet-B3的8.4倍，但在1080Ti上推理速度是后者的1.8倍，即前者的计算密度是后者的15倍。除了Winograd conv带来的加速，FLOPs和推理速度之间的差异可以归因于两点：内存访问成本（memory access cost, MAC）和并行度。多分支结构中分支addition和concatenation的计算量可以忽略不计，但MAC非常大。多分支结构中一个building block中的fragmented operator（即一个卷积运算或一个池化运算）的数量更多，这对GPU等具有强大并行计算能力的设备不友好，例如ResNet中是2或3，而VGG中是1。

        Memory-economical  多分支结构的内存占用效率更低，这是因为每个分支的计算结果要先保存在内存中，直到最终的相加或拼接完成后才释放，从而导致内存占用峰值变大，如下图所示。

         Flexible  多分支的结构需要精心的设计因此缺乏灵活性，比如ResNet中每个block的最后一层卷积的输出必须要保证和输入的大小一致，这样才能通过shortcut和输入相加。另外，多分支结构也让剪枝变得更难。

Training-time Multi-branch Architecture

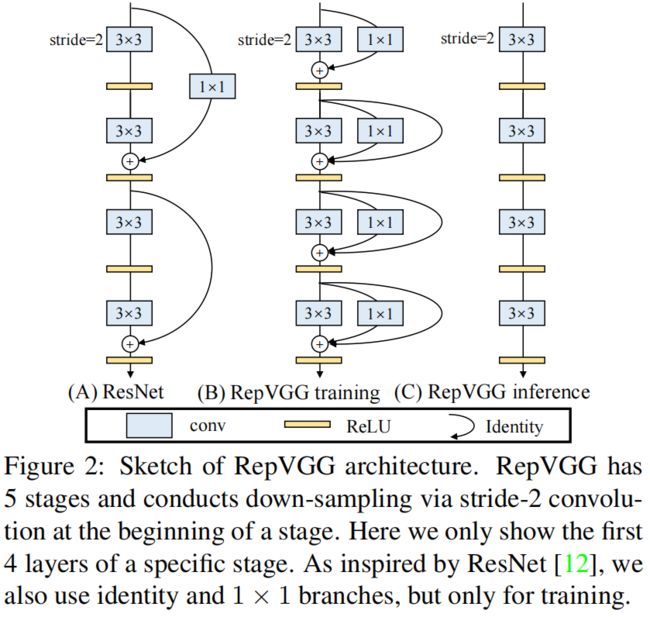
        因为多分支架构的精度更高，因此RepVGG在训练时借鉴ResNet的residual block的结构，具体包括 \(3\times 3\)、\(1\times 1\)、shortcut三个分支，当输入输出的维度不一致即stride=2时，则只有 \(3\times 3\)、\(1\times 1\) 两个分支，如下图所示

Re-param for Plain Inference-time Model

        因为单分支结构推理速度快等优点，在推理阶段通过结构重参数化将训练时的多分支结构等价转换成单分支结构，结构重参数化在作者之前的《ACNet: Strengthening the Kernel Skeletons for Powerful CNN via Asymmetric Convolution Blocks》这篇文章中提出，具体介绍可参考这篇博客 结构重参数化宇宙之一：ACNet_00000cj的博客-CSDN博客。具体来说，我们用 \(W^{(3)}\in \mathbb{R}^{C_{2}\times C_{1}\times 3\times 3}\) 表示一个输入通道为 \(C_{1}\) 输出通道为 \(C_{2}\) 的 \(3\times 3\) 卷积层，\(W^{(1)}\in \mathbb{R}^{C_{2}\times C_{1}}\) 表示 \(1\times 1\)   卷积层，\(\mu^{(3)},\sigma^{(3)},\gamma^{(3)},\beta^{(3)}\) 分别表示 \(3\times 3\) 卷积层后的BN的均值、方差、缩放因子、偏置，\(\mu^{(1)},\sigma^{(1)},\gamma^{(1)},\beta^{(1)}\) 表示 \(1\times 1\) 卷积后的BN参数，\(\mu^{(0)},\sigma^{(0)},\gamma^{(0)},\beta^{(0)}\) 表示identity分支的BN参数。\(M^{(1)}\in \mathbb{R}^{N\times C_{1}\times H_{1}\times W_{1}}\) 和 \(M^{(2)}\in \mathbb{R}^{N\times C_{2}\times H_{2}\times W_{2}}\) 分别表示输入和输出，\(*\) 表示卷积运算，当 \(C_{1}=C_{2},H_{1}=H_{2},W_{1}=W_{2}\) 时，有

当输入输出维度不相等时，没有identity分支，只有式（1）中的前两项。推理时的BN如下所示，其中 \(\forall 1\leq  i\leq C_{2}\)

我们首先把BN和它前面的卷积层合并到一起转换成一个卷积和一个偏置，\(\begin{Bmatrix}
W',b'
\end{Bmatrix}\)是由\(\begin{Bmatrix}
W,\mu,\sigma,\gamma,\beta
\end{Bmatrix}\)转换而来的卷积和偏置，有

很容易验证，\(\forall 1\leq  i\leq C_{2}\)，有 

上面的转换同样可以应用到identity分支，因为identity可以看作核是单位矩阵的 \(1\times 1\) 卷积，转换后我们就有了1个 \(3\times 3\) 卷积，2个 \(1\times 1\) 卷积，3个偏置项，然后把3个偏置相加得到最终的bias，3个卷积相加得到最终的卷积项。这里的卷积相加，具体步骤是首先把两个 \(1\times 1\) 卷积zero-padding成 \(3\times 3\) 卷积，然后再相加，如下图所示

注意，上述转换的前提是 \(3\times 3\) 卷积和 \(1\times 1\) 卷积的步长要相等，同时后者的padding是前者的padding-1，例如通常 \(3\times 3\) 卷积对于输入的padding=1，此时 \(1\times 1\) 卷积的padding=0。

Architectural Specifification

        下表是RepVGG的具体结构，其中和VGG一样只用了 \(3\times 3\) 卷积，但没有使用VGG中的max-pooling因为作者希望整个模型中只有一种操作

整个模型分为5个stage，每个stage的第一层是stride=2的降采样，对于分类任务，最后用全局平均池化和一个全连接层作为head。模型每个stage的层数按以下三个准则来确定：1）第一个stage的输入分辨率较大，比较耗时，因此为了低延迟只设置一层。2）最后一个stage的通道数较多，为了减少参数只设置一层。3）参照ResNet，把最多的层放在倒数第二个stage。RepVGG-A每个stage的层数分别为1,2,4,14,1，RepVGG-B相比于RepVGG-A，在第2,3,4个stage分别多了两层。

        此外，作者还设置了两个缩放因子 \(a,b\) 来定义每一层的宽度，其中 \(a\) 用于前4个stage，\(b\) 用于最后一个stage，且设置 \(b>a\) 因为希望最后一层有更丰富的特征用于分类或其它下游任务。不同配置的RepVGG如下图所示

        为了进一步减少参数和计算量，作者又引入了 \(3\times 3\) 组卷积，对于RepVGG-A，组卷积放置在第3,5,7, ..., 21层，对于RepVGG-B，还额外放在了第23,25,27层。之所以不在相邻的层使用组卷积，是因为ShuffleNet的文章中提到这样会阻碍通道间的信息流动并带来副作用：某个通道的输出只从输入的一小部分通道获得信息。为了方便，组卷积参数 \(g\) 设置为1、2、4，并且同一模型全局使用相同的 \(g\)，并没有按层对 \(g\) 进行调优。

        在ImageNet上分类的实验结果如下所示

可以看出，不论是ResNet-18这样偏轻量的模型，还是如ResNeXt-101这样最先进的大模型，对应配置的RepVGG都可以获得相似或更好的性能，并且速度更快，更不用说RepVGG结构简单、方便定制、容易剪枝优化等其它额外的优点。