t-svd张量分解算法详解
t-svd张量分解算法详解
- 讲解论文
- 所需基础知识
- 背景知识介绍
-
- 什么是svd分解?
-
- 定义1:svd分解
- 什么是张量?
- t-svd分解详解
-
- 正式定义t-svd!
- 疑惑问题
- 解惑前需要学习的定义:
-
- 定义2.1:张量t积
- 疑惑解答:
讲解论文
讲解我们张量分解上面经常说的t-svd内容,原论文题目如下:
Factorization strategies for third-order tensors
论文链接:link
所需基础知识
拥有高中基础水平知识,并且学习了部分矩阵分析内容
背景知识介绍
我们先来规定一些特定的符号,不再在下文重复解释。
| 符号 | 意义 |
|---|---|
| x | 标量(就是单纯的任意一个数) |
| x \mathbf{x} x | 列向量 |
| X X X | 矩阵 |
| X T X^T XT | 矩阵转置 |
| X − 1 X^{-1} X−1 | 矩阵求逆 |
| X \mathcal{X} X | 张量 |
| ⊗ \otimes ⊗ | 克罗内克积 |
什么是svd分解?
首先,我们可能先要知道svd分解是什么东西(当然,可以跳过这一小节呀)。实际上,我们只用把这个svd分解当做一个计算方法来理解就行。就是如果你对一个矩阵用了这种计算方法,你就会得到三个矩阵(知道这个就行啦,当然也要知道这三个矩阵长什么样子)。这三个矩阵长什么样子呢,我们可以看看下面定义:
定义1:svd分解
在矩阵上,假设我们有一个矩阵 A ∈ R I 1 × I 2 A\in R^{I_1\times I_2} A∈RI1×I2,那么我们可以认为,这个矩阵可以有以下形式的分解:
A = U Σ V T A = UΣV^T A=UΣVT
其中,矩阵 U ∈ R I 1 × I 1 U\in R^{I_1\times I_1} U∈RI1×I1和矩阵 V ∈ R I 2 × I 2 V\in R^{I_2\times I_2} V∈RI2×I2是酉矩阵(可以理解为正交矩阵,细节不同可以网上搜一下), Σ ∈ R I 1 × I 2 Σ\in R^{I_1\times I_2} Σ∈RI1×I2矩阵是一个对角矩阵,每个对角线元素是矩阵 A A A的奇异值。(什么是奇异值呢?我们们可以理解为矩阵的一种特征值,有很多关键的特征信息在这些值上面,在矩阵分析里面相当有用。再具体不解释,感兴趣可以网上搜索啦)。

什么是张量?
在我们张量分解领域,张量其实就是高阶的数组。矩阵一般就是二阶张量,然后列向量和行向量就是一阶张量,单纯一个数(标量)就是0阶张量。一个三阶张量 X ∈ R I 1 × I 2 × I 3 \mathcal{X}\in R^{I_1\times I_2\times I_3} X∈RI1×I2×I3(就是你有个数组,是三个维度的,大小是 I 1 × I 2 × I 3 I_1\times I_2\times I_3 I1×I2×I3)。画出图像,就应该是一个立方体。当然,更高阶就是更高维数组。
t-svd分解详解
来,我们直接上手,t-svd长啥样!
正式定义t-svd!
我们假设我们有一个三阶张量 A ∈ R n 1 × n 2 × n 3 \mathcal{A}\in R^{n_1\times n_2\times n_3} A∈Rn1×n2×n3,他身上的数都是实数昂,没考虑虚数情况。那么,我们可以有t-svd分解:
A = U ∗ S ∗ V T \mathcal{A}=\mathcal{U}*\mathcal{S}*\mathcal{V}^T A=U∗S∗VT
其中, U ∈ R n 1 × n 1 × n 3 \mathcal{U}\in R^{n_1\times n_1\times n_3} U∈Rn1×n1×n3和 V ∈ R n 2 × n 2 × n 3 \mathcal{V}\in R^{n_2\times n_2\times n_3} V∈Rn2×n2×n3都是正交张量,然后 m a t h c a l S ∈ R n 1 × n 2 × n 3 mathcal{S}\in R^{n_1\times n_2\times n_3} mathcalS∈Rn1×n2×n3是个对角张量。
我只有一个张量 A \mathcal{A} A,我们怎么计算得到这三个张量呢?
算法如下:

f f t ( ) fft() fft()和 i f f t ( ) ifft() ifft()是matlab的傅里叶变换函数命令,svd也是matlab自带函数。
疑惑问题
蒙了吧,什么又是正交张量?什么又是对角张量?张量符号 ∗ * ∗又是什么意思?凭什么能有这样子形式的分解?为什么这样子计算能够就能够得到这些张量?有什么意义吗这样的分解形式?带着这些疑问,我们慢慢往下看昂。
解惑前需要学习的定义:
我们在解决上面的问题的时候,先来看看原论文给出的一些定义:
如果一个列向量 v \mathbf{v} v:
v = [ v 0 v 1 v 2 v 3 ] T \mathbf{v} = [v_0 \quad v_1\quad v_2 \quad v_3]^T v=[v0v1v2v3]T
然后有循环操作:
c i c r ( v ) = [ v 0 v 3 v 2 v 1 v 1 v 0 v 3 v 2 v 2 v 1 v 0 v 3 v 3 v 2 v 1 v 0 ] cicr(\mathbf{v}) = \left[\begin{array}{llll}v_0 & v_3 & v_2 & v_1 \\ v_1 & v_0 & v_3 & v_2 \\ v_2 & v_1 & v_0 & v_3 \\ v_3 & v_2 & v_1 & v_0\end{array}\right] cicr(v)=⎣⎢⎢⎡v0v1v2v3v3v0v1v2v2v3v0v1v1v2v3v0⎦⎥⎥⎤
这种循环操作 v \mathbf{v} v后得到的矩阵叫做循环矩阵。其实在矩阵分析中,有个公认的事实:假设有个列向量 v ∈ R n × 1 \mathbf{v}\in R^{n \times 1} v∈Rn×1,他的离散傅里叶变换矩阵为 F n ∈ R n × n F_n\in R^{n \times n} Fn∈Rn×n,那么就有
F n c i c r ( v ) F n − 1 F_n cicr(\mathbf{v}) F^{-1}_n Fncicr(v)Fn−1
这个运算得到的是一个对角矩阵。并且对角上的元素都是和你直接对列向量 v \mathbf{v} v进行傅里叶变换得到的元素是一模一样的。
理解:对列向量 v \mathbf{v} v做傅里叶变换,实际就是让 v \mathbf{v} v左乘一个傅里叶变换矩阵 F n F_n Fn。对,没错和上面公式上面的是同一个 F n F_n Fn。也就是 d i a g ( F n v ) = F n c i c r ( v ) F n − 1 diag(F_n \mathbf{v}) =F_n cicr(\mathbf{v}) F^{-1}_n diag(Fnv)=Fncicr(v)Fn−1。其中, d i a g ( ) diag() diag() 函数就是将列向量重新排列成一个对角矩阵。具体为什么会相等呢,有兴趣的小伙伴可以自己手推一下,看一下傅里叶变换矩阵的性质,实际上是相等的。懒得推导不太相信的小伙伴也可以用matlab或者其他代码验证一项左边右边是否相等就行。记住这个公式,拿来用就行。
假设现在有一个三阶张量 A ∈ R n 1 × n 2 × n 3 \mathcal{A}\in R^{n_1\times n_2\times n_3} A∈Rn1×n2×n3,那么我们定义:
circ ( A ) = [ A 1 A n 3 A n 3 − 1 … A 2 A 2 A 1 A n 3 … A 3 ⋮ ⋱ ⋱ ⋱ ⋮ A n 3 A n 3 − 1 ⋱ A 2 A 1 ] , \operatorname{circ}(\mathcal{A})=\left[\begin{array}{ccccc} A_1 & A_{n_3} & A_{n_3-1} & \ldots & A_2 \\ A_2 & A_1 & A_{n_3} & \ldots & A_3 \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ A_{n_3} & A_{n_3-1} & \ddots & A_2 & A_1 \end{array}\right] \text {, } circ(A)=⎣⎢⎢⎢⎡A1A2⋮An3An3A1⋱An3−1An3−1An3⋱⋱……⋱A2A2A3⋮A1⎦⎥⎥⎥⎤,
其中, A i A_i Ai表示的是张量 A \mathcal{A} A的第 i i i个前向切片,数学上写出来是 A ( : , : , i ) \mathcal{A}(:,:,i) A(:,:,i),在matlab上你可以读作:数组 A \mathcal{A} A的全部行的全部列的第i个矩阵。可能你会说还有什么 A ( i , : , : ) \mathcal{A}(i,:,:) A(i,:,:)、 A ( : , i , : ) \mathcal{A}(:,i,:) A(:,i,:),为了不影响记忆顺序,不会介绍他们的学术名字,只要记得 A ( : , : , i ) \mathcal{A}(:,:,i) A(:,:,i)是前向切片就行,用 A i A_i Ai表示。
再来个定义:
MatVec ( A ) = [ A 1 A 2 ⋮ A n 3 ] , \operatorname{MatVec}(\mathcal{A})=\left[\begin{array}{ccccc} A_1 \\ A_2\\ \vdots \\ A_{n_3} \end{array}\right] \text {, } MatVec(A)=⎣⎢⎢⎢⎡A1A2⋮An3⎦⎥⎥⎥⎤,
如果你将 M a t V e c ( A ) MatVec(\mathcal{A}) MatVec(A)折叠起来,你就会得到原来的张量 A \mathcal{A} A啦。折叠的这个操作,我们就叫fold,数学写为:
f l o d ( M a t V e c ( A ) ) = A , flod(MatVec(\mathcal{A})) = \mathcal{A}, flod(MatVec(A))=A,
ok,那么我们其实又可以有公式:
( F n 3 ⊗ I n 1 ) ⋅ circ ( MatVec ( A ) ) ⋅ ( F n 3 − 1 ⊗ I n 2 ) = [ D 1 D 2 ⋱ D n 3 ] , \left(F_{n_3} \otimes I_{n_1}\right) \cdot \operatorname{circ}(\operatorname{MatVec}(A)) \cdot\left(F_{n_3}^{-1} \otimes I_{n_2}\right)=\left[\begin{array}{llll} D_1 & & & \\ & D_2 & & \\ & & \ddots & \\ & & & D_{n_3} \end{array}\right], (Fn3⊗In1)⋅circ(MatVec(A))⋅(Fn3−1⊗In2)=⎣⎢⎢⎡D1D2⋱Dn3⎦⎥⎥⎤,
其中, ⊗ \otimes ⊗表示克罗内克积(矩阵分析里面的一种运算,不会的或者忘记的同学百度一下昂)。这个公式也是很有意思呀,大家可以在草稿纸上写一下元素乘积的形式,就会惊奇发现,实际上就是对张量 A \mathcal{A} A的每个前向切面对应位置的元素组成的列向量都做了一次傅里叶变换(这个句话很重要,理解了就明白t-svd了一大半啦)。
坚持住,再学一点定义,你就可以全部都明白了。
定义2.1:张量t积
假设我们现在有两个张量,分别是 A ∈ R n 1 × n 2 × n 3 \mathcal{A}\in R^{n_1\times n_2\times n_3} A∈Rn1×n2×n3和 B ∈ R n 2 × l × n 3 \mathcal{B}\in R^{n_2\times l \times n_3} B∈Rn2×l×n3,然后定义他们的t积为:
A ∗ B = fold ( circ ( A ) ) ⋅ MatVec ( B ) ) \mathcal{A} * \mathcal{B}=\operatorname{fold}(\operatorname{circ}(\mathcal{A})) \cdot \operatorname{MatVec}(\mathcal{B})) A∗B=fold(circ(A))⋅MatVec(B))
举个例子:假设分别是 A ∈ R n 1 × n 2 × 3 \mathcal{A}\in R^{n_1\times n_2\times 3} A∈Rn1×n2×3和 B ∈ R n 2 × l × 3 \mathcal{B}\in R^{n_2\times l \times 3} B∈Rn2×l×3,然后有:
A ∗ B = fold ( [ A 1 A 3 A 2 A 2 A 1 A 3 A 3 A 2 A 1 ] [ B 1 B 2 B 3 ] ) ∈ R n 1 × ℓ × 3 \mathcal{A} * \mathcal{B}=\text { fold }\left(\left[\begin{array}{ccc} A_1 & A_3 & A_2 \\ A_2 & A_1 & A_3 \\ A_3 & A_2 & A_1 \end{array}\right]\left[\begin{array}{l} B_1 \\ B_2 \\ B_3 \end{array}\right]\right) \in \mathbb{R}^{n_1 \times \ell \times 3} A∗B= fold ⎝⎛⎣⎡A1A2A3A3A1A2A2A3A1⎦⎤⎣⎡B1B2B3⎦⎤⎠⎞∈Rn1×ℓ×3
疑惑解答:
ok,实际上你已经知道张量运算 ∗ * ∗是什么操作了,已经解决了一个问题啦。
然后我们又来回顾一下,他们的形式和分解的计算方法:
形式:
A = U ∗ S ∗ V T \mathcal{A}=\mathcal{U}*\mathcal{S}*\mathcal{V}^T A=U∗S∗VT
计算算法:
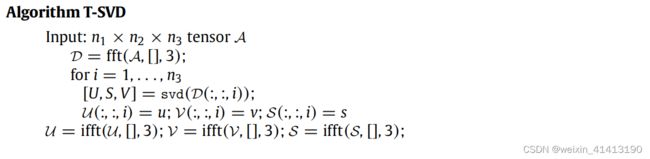
那么,还有个很自然的问题,就是为什么可以通过上面的算法计算得到 A \mathcal{A} A分解出来的三个因子张量呢?运用我们前面学的定义,就可以证明啦,证明如下。
证明:
通过前面定义,我们计算 c i r c ( A ) circ(\mathcal{A}) circ(A)循环矩阵,做傅里叶变后取转换成对角阵(就是下面这个运算):
( F n 3 ⊗ I n 1 ) ⋅ circ ( MatVec ( A ) ) ⋅ ( F n 3 − 1 ⊗ I n 2 ) = [ D 1 D 2 ⋱ D n 3 ] , \left(F_{n_3} \otimes I_{n_1}\right) \cdot \operatorname{circ}(\operatorname{MatVec}(A)) \cdot\left(F_{n_3}^{-1} \otimes I_{n_2}\right)=\left[\begin{array}{llll} D_1 & & & \\ & D_2 & & \\ & & \ddots & \\ & & & D_{n_3} \end{array}\right], (Fn3⊗In1)⋅circ(MatVec(A))⋅(Fn3−1⊗In2)=⎣⎢⎢⎡D1D2⋱Dn3⎦⎥⎥⎤,
然后我们对每个 D i D_i Di都做一次svd分解,我们就可以有
[ D 1 ⋱ D n 3 ] = [ U 1 ⋱ U n 3 ] [ Σ 1 ⋱ Σ n 3 ] [ V 1 T ⋱ V n 3 T ] . \left[\begin{array}{ccc} D_1 & & \\ & \ddots & \\ & & D_{n_3} \end{array}\right]=\left[\begin{array}{lll} U_1 & & \\ & \ddots & \\ & & U_{n_3} \end{array}\right]\left[\begin{array}{ccc} \Sigma_1 & & \\ & \ddots & \\ & & \Sigma_{n_3} \end{array}\right]\left[\begin{array}{lll} V_1^T & & \\ & \ddots & \\ & & V_{n_3}^T \end{array}\right] \text {. } ⎣⎡D1⋱Dn3⎦⎤=⎣⎡U1⋱Un3⎦⎤⎣⎡Σ1⋱Σn3⎦⎤⎣⎡V1T⋱Vn3T⎦⎤.
ok,我们再对上面公式每个大矩阵都左乘 ( F n 3 ⊗ I n 2 ) (F_{n_3}^ \otimes I_{n_2}) (Fn3⊗In2),右乘 F n 3 − 1 ⊗ I n 2 F_{n_3}^{-1} \otimes I_{n_2} Fn3−1⊗In2,你就会惊奇发现,式子左边我们就可以得到回来的张量 A \mathcal{A} A了,右边也相当于每个大矩阵都做了一次傅里叶逆变换。也就是说,我们实际就是先对张量 ( A ) \mathcal(A) (A)做一次循环展开,再做傅里叶变换,然后对每个对角的小矩阵做svd分解,分解后再逆变换回去,就还是原始 A \mathcal{A} A。这个过程实际也是上面图片算法过程了。
ok,实际上最核心的东西相信你已经明白了。当然t-svd还有一些很好玩的性质呀,比如他们张量 U \mathcal{U} U和 V \mathcal{V} V都是正交张量,正交张量怎么定义的,为什么他们是正交张量呀等等这些不再继续深入讲解啦,都比较简单,可以回到原论文找到答案。
然后还有个问题是,有什么用呢?这种算法实际将矩阵卷积发挥到了一定的优势,在数据压缩、张量补全上面,都有着很大优势。目前主流TT、TR、FCTN、TW分解都是很普通的线性组合,虽然这个也是线性组合,但是他却考虑了卷积。实际上,他在张量补全上面恢复效果惊人,并且拥有着很快运算速度。
欢迎各位大佬指正和点评,谢谢。