Kaggle 机器学习实战 朴素贝叶斯（原理+西瓜数据集实战）

Kaggle 机器学习实战 朴素贝叶斯（原理+西瓜数据集实战）

朴素贝叶斯概念

（这一部分来自于国科大网安学院的PPT以及周志华的机器学习，需要的可在文章末尾加公号 AC粥 回复 2022秋机器学习 （其中第二章就是贝叶斯学习）；回复 西瓜书 获取周志华机器学习）

基础

类别先验概率的估计，即某一类的数量占总体数量的比例
$$P(c)=\frac{D_c}{D}$$
类别概率密度估计，即类条件概率，分两种情况

​ $x_i$离散情况：$D_{c,x_i}$表示$D_c$在第$i$个属性上取值为$x_i$的样本组成的集合
$$P(x_i|c)=\frac{D_{c,x_i}}{D_c}$$
​ $x_i$连续情况：由某一概率密度估计类别概率
$$p(x_i|c)=\frac{1}{\sqrt{2\pi }{\sigma }_{c,i}}exp(-\frac{(x_i-{\mu }_{c,i}{)}^2}{2{\sigma }_{c,i}^2})$$

$$P(x_1,x_2,x_3,...,x_n)=P(x_1)\times P(x_2|x_1)\times P(x_3|x_1,x_2)\times ...\times P(x_n|x_1,x_2,...,x_{n-1})$$

$k$个类别，$d$个属性：$P(c_j)$和$P(x_i|c_j)$，（$i=1,...,d$个属性，$j=1,...,k$），共$1+d\times k$个概率分布要统计。

拉普拉斯平滑

在实际情况中，我们可能因为样本不充分而导致概率估计值为0。例如，

中$|D_c=0|$（某一类没有）,$|D_{c,x_i}|=0$（某一类中属性$x_i$的某一取值不存在，样本不充分导致），而且它们一旦为0整个概率就为0。

拉普拉斯平滑的具体做法为
$$\begin{gathered} \hat{P}(c)=\frac{|D_c|+1}{|D|+N},N为类别数 \\ \widehat{P(x_i|c)}=\frac{|D_{c,x_i}|+1}{|D_c|+N_i},N_i为x_i的可能取值个数 \end{gathered}$$

例子说明

描述

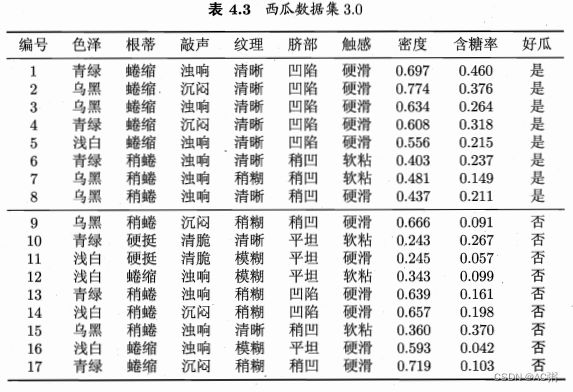
以下是西瓜数据集，显然类别只有两类，分别是好瓜[是，否]。

现在我们有测试样例：

编号	色泽	根蒂	敲声	纹理	脐部	触感	密度	含糖率	好瓜
测试1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	0.697	0.460	？

对于类先验概率，有
$$\begin{gathered} P(好瓜=是)=\frac{8}{17}\approx 0.471, \\ P(好瓜=否)=\frac{9}{17}\approx \mathrm{0.529.} \end{gathered}$$
估计类条件概率，有（未用拉普拉斯平滑）

为什么$p_{密度:0.697|是}\approx 1.959>1$？注意，这是概率密度，对于连续变量来说，越靠近均值概率密度越大，相同的区间概率越大，所以可以用概率密度。

可以看到上文中并没有统计敲声这个属性，为什么呢？
$$P_{清脆|是}=P(敲声=清脆|好瓜=是)=\frac{0}{8}=0$$
敲声这个属性有存在0的情况，应该用拉普拉斯平滑。

类先验概率重写为：
$$\hat{P}(好瓜=是)=\frac{8+1}{17+2}\approx 0.474,\hat{P}(好瓜=否)=\frac{9+1}{17+2}\approx 0.526$$
类条件概率如$P_{清脆|是}$可估计为：
$${\hat{P}}_{清脆|是}=\hat{P}(敲声=清脆|好瓜=是)=\frac{0+1}{8+3}\approx 0.091$$

代码

这个代码整理后可以不限制数据集，按照规定形式制作数据集即可。

写的有点冗余。。。

import numpy as np

original_data = '编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜\n\
1,青绿,蜷缩,浊响,清晰,凹陷,硬滑,0.697,0.46,是\n\
2,乌黑,蜷缩,沉闷,清晰,凹陷,硬滑,0.774,0.376,是\n\
3,乌黑,蜷缩,浊响,清晰,凹陷,硬滑,0.634,0.264,是\n\
4,青绿,蜷缩,沉闷,清晰,凹陷,硬滑,0.608,0.318,是\n\
5,浅白,蜷缩,浊响,清晰,凹陷,硬滑,0.556,0.215,是\n\
6,青绿,稍蜷,浊响,清晰,稍凹,软粘,0.403,0.237,是\n\
7,乌黑,稍蜷,浊响,稍糊,稍凹,软粘,0.481,0.149,是\n\
8,乌黑,稍蜷,浊响,清晰,稍凹,硬滑,0.437,0.211,是\n\
9,乌黑,稍蜷,沉闷,稍糊,稍凹,硬滑,0.666,0.091,否\n\
10,青绿,硬挺,清脆,清晰,平坦,软粘,0.243,0.267,否\n\
11,浅白,硬挺,清脆,模糊,平坦,硬滑,0.245,0.057,否\n\
12,浅白,蜷缩,浊响,模糊,平坦,软粘,0.343,0.099,否\n\
13,青绿,稍蜷,浊响,稍糊,凹陷,硬滑,0.639,0.161,否\n\
14,浅白,稍蜷,沉闷,稍糊,凹陷,硬滑,0.657,0.198,否\n\
15,乌黑,稍蜷,浊响,清晰,稍凹,软粘,0.36,0.37,否\n\
16,浅白,蜷缩,浊响,模糊,平坦,硬滑,0.593,0.042,否\n\
17,青绿,蜷缩,沉闷,稍糊,稍凹,硬滑,0.719,0.103,否'


def is_digit(s):
    try:
        float(s)
        return True
    except ValueError:
        pass
    return False


def preprocess_data(data):
    data = data.split("\n")[1:] # 分成拥有几个属性的输入，并去掉编号,色泽,根蒂,敲声,纹理,脐部,触感,密度,含糖率,好瓜
    data = [data[j].split(",") for j in range(len(data))] # 去掉编号
    data = [data[j][1:] for j in range(len(data))]
    data = np.array(data).T
    # x是维度，y是标签
    x, y = data[:-1], data[-1].tolist()
    class_y = list(set(y))
    class_y.sort(key=y.index)
    x = x.T
    x = x.tolist()
    original_class_data = list()  # 记录每个属性的可能取值，如果是浮点数即连续值，那么直接返回浮点数
    float_class = list()  # 记录连续值所在维度
    discrete_class = list()  # 记录离散值所在维度
    class_data = list()
    for i in range(len(data)):
        temp_list_data = list()
        flag = is_digit(data[i][0])
        if not flag:
            for temp_data in data[i]:
                if temp_data not in temp_list_data:
                    temp_list_data.append(temp_data)
            discrete_class.append(i)
        else:
            if data[i][0].count(".") == 0:  # 如果是整数，那么是离散值
                temp_list_data = [int(i) for i in data[i]]
                discrete_class.append(i)
            else:  # 如果是浮点数，那么是连续值
                temp_list_data = [float(i) for i in data[i]]
                float_class.append(i)
        original_class_data.append(temp_list_data)
    discrete_class = discrete_class[:-1]
    if not is_digit(original_class_data[-1][0]):
        y = [original_class_data[-1].index(j) for j in y]
    else:
        y = [int(j) for j in y]
    for i in range(len(x)):
        for j in range(len(x[i])):
            if j not in float_class:
                x[i][j] = original_class_data[j].index(x[i][j])
            else:
                x[i][j] = original_class_data[j][i]
    for i in discrete_class:
        class_data.append([])
        for j in range(len(original_class_data[i])):
            class_data[i].append(j)
    for i in float_class:
        class_data.append(original_class_data[i])

    print("x", x)
    print("y", y)
    print("class_y", class_y)
    print("original_class_data", original_class_data)
    print("class_data", class_data)
    print("float_class", float_class)
    print("discrete_class", discrete_class)
    return x, y, original_class_data, float_class, class_y, discrete_class, class_data

# 将同一个输出归为同一类
def product_dict_y(y):
    dict_y = {}
    for i in range(len(y)):
        if y[i] not in dict_y:
            dict_y[y[i]] = []
        dict_y[y[i]].append(i)
    return dict_y


x, y, original_class_data, float_class, class_y, discrete_class, class_data = preprocess_data(original_data)

class_y_to_number = [i for i in range(len(class_y))]
print("temp_x", *x)
tranverse_x = list(map(list, zip(*x)))
print("tranverse_x", tranverse_x)
dict_y = product_dict_y(y)
print("dict_y", dict_y)
property_to_class = []

### 输出每一类中每个属性每个取值的概率，连续属性只需要计算均值和标准差
import copy
for i in dict_y:
    property_to_class.append(copy.deepcopy(class_data))
for i in dict_y:
    len_per_tranverse_x = len(dict_y[i])
    for k in discrete_class:
        len_per_class_data = len(class_data[k])
        temp_certain_class = [tranverse_x[k][s] for s in dict_y[i]]  # 表示tranverse某一属性中属于该类的元素

        for m in class_data[k]:
            property_to_class[i][k][m] = (temp_certain_class.count(m) + 1) * 1.0 / (len_per_class_data + len_per_tranverse_x)

    for k in float_class:
        temp_certain_class = [tranverse_x[k][s] for s in dict_y[i]]

        mean = np.mean(temp_certain_class)
        std = np.std(temp_certain_class)
        property_to_class[i][k] = [mean, std]

possibility_y = []
for i in dict_y:
    possibility_y.append((len(dict_y[i]) + 1) / (len(y)+len(dict_y)))
print("每一类的概率", possibility_y)
print("每一类中每个属性取值的概率", property_to_class)


# 将测试的输入转换成编码形式，
def translate_to_normal(x, original_class_data, float_class, discrete_class):
    new_discrete_x = []
    new_float_x = []
    for i in discrete_class:
        new_discrete_x.append(original_class_data[i].index(x[i]))
    for i in float_class:
        new_float_x.append(float(x[i]))
    return new_discrete_x, new_float_x


# 离散取值从这里面选，
# [['青绿', '乌黑', '浅白'], ['蜷缩', '稍蜷', '硬挺'], ['浊响', '沉闷', '清脆'], ['清晰', '稍糊', '模糊'], ['凹陷', '稍凹', '平坦'], ['硬滑', '软粘']]
# 连续取值 > 0
x = ["青绿", "蜷缩", "沉闷", "清晰", "凹陷", "硬滑", "0.45", "0.883"]

new_discrete_x, new_float_x = translate_to_normal(x, original_class_data, float_class, discrete_class)
print("编码后的离散属性取值", new_discrete_x)
print("编码后的连续属性取值", new_float_x)

import math


### 将输入转换成编码格式后，按照property_to_class 的概率得到每一类的概率（非实际概率，没有分母）
def test(x, property_to_class,possibility_y, float_class, disctrete_class, original_class_data):
    new_discrete_x, new_float_x = translate_to_normal(x, original_class_data, float_class, discrete_class)

    final_possiblity = []
    for i in range(len(possibility_y)):
        temp = math.log(math.e, possibility_y[i])
        for j in range(len(disctrete_class)):
            temp = temp + math.log(property_to_class[i][disctrete_class[j]][new_discrete_x[j]])
        for j in range(len(float_class)):
            temp_float = new_float_x[j]
            mean = property_to_class[i][float_class[j]][0]
            std = property_to_class[i][float_class[j]][1]
            temp = temp + math.log(math.e, 1 / (math.sqrt(2 * math.pi) * std) * math.exp(-(temp_float - mean) ** 2 / (2 * std * std)) )
        final_possiblity.append(temp)
    return final_possiblity


final_possibility = test(x, property_to_class, possibility_y, float_class, discrete_class, original_class_data)
### 输出最大的”概率“（非实际概率，没有分母）
print(class_y[final_possibility.index(max(final_possibility))])

关注公众号 AC粥 ，回复 Kaggle 机器学习实战 朴素贝叶斯（原理+西瓜数据集） 获取本文的markdown源码