卷积神经网络CNN特点功能及其缺陷

卷积神经网络（CNN）中的模块及其功能作用

CNN的目的

CNN的目的是以一定的模型对事物进行特征提取，而后根据特征对该事物进行分类、识别、预测或决策等。最重要的步骤在于特征提取，即如何提取到能最大程度区分事物的特征，实现这个伟大的模型的，需要对CNN进行迭代训练。

特征

在图像中（举个例子），目标事物的特征主要体现在像素与像素之间的关系。比如在图像识别中，图片中猫身体毛发对应的像素之间会比毛发与背景之间像素的区别较大，这样便可以将图片中的“猫”识别出来。

在CNN中，大部分特征提取依赖于卷积运算。

卷积与特征提取

卷积在此其实就是内积，步骤很简单，就是根据多个一定的权重（即卷积核），对一个块的像素进行内积运算，其输出就是提取的特征之一：

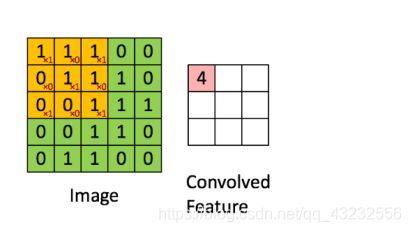
卷积的特点：局部感知、参数共享、多核

局部感知，简单来说，卷积核的大小一般小于输入图像的大小（如果等于则是全连接），因此卷积提取出的特征会更多地关注局部 —— 这很符合日常我们接触到的图像处理。而每个神经元其实没有必要对全局图像进行感知，只需要对局部进行感知，然后在更高层将局部的信息综合起来就得到了全局的信息。
参数共享，参数共享最大的作用莫过于很大限度地减少运算量了。
多核，一般我们都不会只用一个卷积核对输入图像进行过滤，因为一个核的参数是固定的，其提取的特征也会单一化。这就有点像是我们平时如何客观看待事物，必须要从多个角度分析事物，这样才能尽可能地避免对该事物产生偏见。我们也需要多个卷积核对输入图像进行卷积。

Down-Pooling

卷积后再接上一个池化层（Pooling）是很好的搭配，能很好的聚合特征、降维来减少运算量。

多层卷积

层数越高，提取到的特征就越全局化。

池化

池化，即对一块数据进行抽样或聚合，例如选择该区域的最大值（或平均值）取代该区域的整体特征。

激活函数的意义

激活函数的作用就是将输入数据映射到0到1上（tanh是映射-1到+1上）。至于映射的原因，除了对数据进行正则化外，大概是控制数据，使其只在一定的范围内。当然也有另外细节作用，例如Sigmoid（tanh）中，能在激活的时候，更关注数据在零（或中心点）前后的细小变化，而忽略数据在极端时的变化，例如ReLU还有避免梯度消失的作用。通常，Sigmoid（tanh）多用于全连接层，而ReLU多用于卷积层。

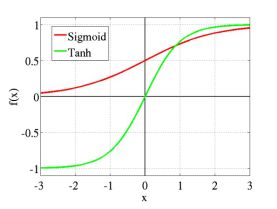
换个角度来看待这个激活函数，如果我们把每一次激活动作当成一次分类，即对输入数据分成两类（0或1），那么激活函数得到的输出是在0到1的值，它可以代表着这次“分类”的归属度。如果我们把0规定为未激活，1表示激活，那么输出0.44就表示激活了44%。而激活函数的使用却有可能带来一定的负面影响（对于训练的负面影响），激活函数可能会使我们得输入数据都激活了大半，对此我们有另外的对策 —— LRN。

LRN的催化与抑制

LRN，局部响应归一化。在神经学科中，有一个叫横向抑制（lateral inhibition）的概念，这种抑制的作用就是阻止兴奋神经元向邻近神经元传播其动作趋势，从而减少兴奋神经元的邻近神经元的激活程度。我们使用LRN层来对激活函数的输出数据进行横向抑制，在为激活函数收拾残局的同时，LRN还凸显了该区域的一个峰值 —— 这个峰值特征就是我们想要的特征。

特别是ReLU，它无限制的激活使得我们更需要LRN来到数据进行归一化。在大规模的数据中，我们大多情况下更看重被凸显的高频特征。因此，用LRN对数据的峰值进行催化而对其周围进行抑制，至关重要。

在许多CNN的后部分，都存在着一个IP（Inner Product）层/内积层/fc（full connect）层/全连接层。在许多论文中，它替代了softmax来特征负责最终的提取，而有人也指出CNN最后可以不用IP层。

Dropout的作用

Dropout的任务就是在训练时，通过设置阈值并与某些隐含层节点的权重对比，让特定的权重不工作 —— 在该层舍弃这些权重。Dropout的作用也很明显，除了加速运算外，就是防止过拟合了。

卷积神经网络中的局部连接

所谓局部连接，就是卷积层的节点仅仅和其前一层的部分节点相连接，只用来学习局部特征。局部感知采用部分神经元接受信息，再通过综合全部的信息达到增强信息的目的。从下图中我们可以看到，第n+1层的每个节点只与第n层的3个节点相连接，而非与前一层全部5个神经元节点相连，这样原本需要53=15个权值参数，现在只需要33=9个权值参数，减少了40%的参数量，同样，第n+2层与第n+1层之间也用同样的连接方式。这种局部连接的方式大幅减少了参数数量，加快了学习速率，同时也在一定程度上减少了过拟合的可能。

卷积神经网络中的权值共享

权值共享，在深度学习的图像处理任务中表现，可以认为是卷积神经网络中的权值共享。那么权值共享有什么作用呢？答案是可以减少参数的个数。

对于一张输入图片，大小为W×H，如果使用全连接神经网络，生成一张X×Y的feature map，需要W×H×X×Y个参数，按原图长宽为10² ~ 10³级别，XY大小同WH数量级，那么这样一层网络需要的参数个数便是10⁸~10¹²以上。

如何减少参数呢？输出层feature map上的每一个像素，他与原图片的每一个像素都有连接，每一个链接都需要一个参数。但注意到图像一般都是局部相关的，那么如果输出层的每一个像素只和输入层图片的一个局部相连，那么需要参数的个数就会大大减少。假设输出层每个像素只与输入图片上FF的一个小方块有连接，也就是说输出层的这个像素值，只是通过原图的这个FF的小方形中的像素值计算而来，那么对于输出层的每个像素，需要的参数个数就从原来的W * H减小到了F * F。如果对于原图片的每一个F * F的方框都需要计算这样一个输出值，那么需要的参数只是XYF*F，如果feature map长宽是10²级别，而F在10以内的话，那么需要的参数的个数只有10⁵~ 10⁶级别，相比于原来的10⁸~10¹²小了很多很多。

图片还有另外一个特性：图片的底层特征是与特征在图片中的位置无关的。比如说边缘，无论是在图片中间的边缘特征，还是在图片边角处的边缘特征，都可以用过类似于微分的特称提取器提取。那么对于主要用于提取底层特称的前几层网络，把上述局部全连接层中每一个F * F方形对应的权值共享，就可以进一步减少网络中参数的个数。也就是说，输出层的每一个像素，是由输入层对应位置的FF的局部图片，与相同的一组FF的参数（或称权值）做内积，再经过非线性单元计算而来的。这样的话无论图片原大小如何，只用F * F个参数就够了，也就是几个几十个的样子。当然一组F*F的参数只能得到一张feature map，一般会有多组参数，分别经过卷积后就可以有好几层feature map。

高级特征一般是与位置有关的，比如一张人脸图片，眼睛和嘴位置不同，那么处理到高层，不同位置就需要用不同的神经网络权重，这时候卷积层就不能胜任了，就需要用局部全连接层和全连接层。

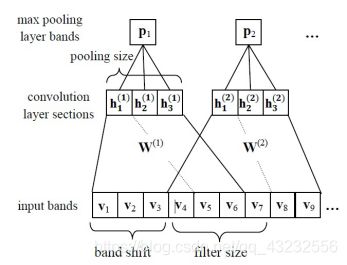
上图示意了局部连接，每一个W只与输入的一部分连接，如果W1和W2是相同的，那么就是卷积层，这时参数W1和W2相同，因此说共享。

全连接层的权重矩阵的大小是固定的，即每一次feature map的输入过来必须都得是一定的大小（即与权重矩阵正好可以相乘的大小），所以网络最开始的输入图像尺寸必须固定，才能保证传送到全连接层的feature map的大小跟全连接层的权重矩阵匹配。

卷积层就不需要固定输入feature map的大小了，因为它只是对局部区域进行窗口滑动，所以用卷积层取代全连接层成为了可能。

卷积神经网络的平移不变性

简单地说，卷积+最大池化约等于平移不变性。
卷积：简单地说，图像经过平移，相应的特征图上的表达也是平移的。

下图只是一个为了说明这个问题的例子。输入图像的左下角有一个人脸，经过卷积，人脸的特征（眼睛，鼻子）也位于特征图的左下角。

在神经网络中，卷积被定义为不同位置的特征检测器，也就意味着，无论目标出现在图像中的哪个位置，它都会检测到同样的这些特征，输出同样的响应。比如人脸被移动到了图像左下角，卷积核直到移动到左下角的位置才会检测到它的特征。

池化：比如最大池化，它返回感受野中的最大值，如果最大值被移动了，但是仍然在这个感受野中，那么池化层也仍然会输出相同的最大值。这就有点平移不变的意思了。

所以这两种操作共同提供了一些平移不变性，即使图像被平移，卷积保证仍然能检测到它的特征，池化则尽可能地保持一致的表达。

卷积的平移不变性就是通过卷积+池化以后不管某一特征移动了位置，总可以检测出来输入到下一层中，又由于全连接是加权求和计算，被CNN激活的特征又可以传导到下一层中。

卷积的缺陷

反向传播
反向传播算法并不是一个深度学习中的高效算法，因为它对数据量的需求很大。

平移不变性
当我们说平移不变性时，我们意思是，稍微改变同一物体的朝向或位置，可能并不会激活那些识别该物体的神经元。假如一个神经元是用来识别一只猫的，其参数会随着猫的位置和转动的变化而变化。虽然数据扩增(data augmentation)在一定程度上解决了这个问题，但这个问题并没有得到彻底的解决。

池化层
池化层的存在会导致许多非常有价值的信息的丢失，同时也会忽略掉整体与部分之间的关联。比如，当我们使用脸部探测器时，我们必须把一些特征结合在一起（嘴，双眼，脸的轮廓和鼻子）才能识别这张脸。

CNN的判别方式是，如果这5个特征同时呈现的概率很高，那这就将是一张人脸。 合并图层，合并层是一个很大的错误，因为它丢失了大量有价值的信息，如果我们正在谈论一个人脸识别器，它会忽略部分和整体之间的关系，所以我们必须结合一些特征（嘴巴，双眼，椭圆的脸和鼻子）才能说明是一张脸。

结论
CNN很厉害，但它还是有两个非常危险的缺陷：平移不变性和池化层。不过，我们可以尝试通过数据扩增等方法来避免潜在的缺陷。

现在，胶囊网络等新的结构的出现正在给深度学习领域带来一场革命。未来，更多改进过的事物会诞生。

坐标建模的任务上（如目标检测、图像生成等）的缺陷

卷积神经网络拥有权重共享、局部连接和平移等变性等非常优秀的属性，使其在多种视觉任务上取得了极大成功。但在涉及坐标建模的任务上（如目标检测、图像生成等），其优势反而成为了缺陷，并潜在影响了最终的模型性能。

卷积神经网络在坐标变换、目标检测等都发挥了重大的作用，但却在一些简单的任务上，却不尽如人意，比如在一个微小的图像中绘制一个像素。论文《An Intriguing Failing of Convolutional Neural Networks and the CoordConv Solution》揭示并分析了卷积神经网络在变换两种空间表征（笛卡尔空间坐标 (i, j) 和 one-hot 像素空间坐标）时的常见缺陷。结果出人意料，因为这项任务看起来如此简单，但其重要性非同一般，因为解决很多常见问题（如在图像中检测目标、训练图像生成模型、从像素中训练强化学习智能体等）都要用到此类坐标变换。结果表明，这些任务可能一直受到卷积缺陷的影响，而改方法在使用之前提出的一个名为 CoordConv 的层作为解决方案时，展示了各方面的性能提升。

发现一：监督渲染对于 CNN 来说并非易事
设想一个简单的任务——监督渲染，在该任务中，我们给出一个 (i, j) 位置作为网络的输入，使其生成一个 64x64 的图像，并在确定位置绘有一个正方形，如图 1a 所示，你要使用何种类型的网络来完成这个任务？

我们可以选用许多图像生成研究论文中使用的方法，使用一堆解卷积（转置卷积）层绘制这个正方形。为了测试这一想法，我们创建了一个数据集，该数据集包含一些随机放置的 9x9 的正方形和一个 64x64 的画布，如图 1b 所示。穷举所有可能的完全可见的正方形得到一个含有 3136 个样本的数据集。为评估模型的泛化能力，我们定义两种训练/测试分割：一种是均匀分割，即将所有可能的中心区域随机分为训练集和测试集，二者的比例为 8:2；另一种是象限分割，即画布被分为四个象限：集中在前三个象限中的小方块被放入训练集，最后一个象限中的小方块被放入测试集。两种数据集分割方法的分布见下图 1c：

图 1.（a）监督渲染任务要求网络根据正方形的 (i, j) 位置绘制正方形。（b）为示例数据点和、（c）展示了按均匀或象限分割训练集与测试集的可视化。

我们原本以为 CNN 可以轻而易举地完成该任务，因为第一，这一任务如此简单（整个数据集可能只需要两行 Python 代码就能生成，如我们的论文所示），第二，这个数据集如此之小，我们可以轻易使用过参数化的模型。但结果表明，CNN 的表现令人大跌眼镜。即使参数高达 1M 且训练时间超过 90 分钟的模型（图 2b）也无法在均匀分割的测试集上获得 0.83 以上的 IOU，或在象限分割上获得 0.36 以上的 IOU（图 2a）。

图 2：（a）在均匀分割和象限分割时的训练和测试的监督渲染任务的 IoU 结果。没有模型能达到 1.0 的 IOU，（b）训练最好的模型之一需要花 90 分钟类达到 0.8 的 IOU。

发现二:CNN 很难解决有监督坐标分类
如果通过直接监督训练渲染如此困难，那么当转换为无监督学习将使问题变得更加具挑战性，例如在相同数据上通过由鉴别器提供的损失训练生成对抗网络（GAN）。

现在我们可以缩小问题范围，以找出哪些因素给这个问题带来了挑战。我们现在要求网络生成一个简单的像素而不再是 9×9 的像素。其实给定解决单像素任务的方法，我们可以进一步使用转置卷积将这一个像素扩展到拥有较多像素的方块，这一直观想法也通过我们的实验得到证实。因此我们建立了有监督坐标分类任务（图 3a），其中数据集由成对的（i, j）坐标轴和带有单个激活像素的图像组成，如下图 3b 所示：

图 3：（a）有监督坐标轴分类要求网络在给定位置（i, j）的情况下生成单个像素。（b）展示了样本数据点，（c）展示了分割训练和测试集的可视化。

我们使用不同的超参数训练了非常多的网络，并观察到即使一些网络能记住训练集，但它们从没有超过 86% 的测试准确率（图 4a）。这样的准确率花了一个多小时进行训练才得到。

我们期望卷积能完美地处理这个问题，但实际上它并不行。为了弄清楚卷积网络到底是在做什么，我们采用已训练最好的网络并检验它的预测。

我们要求网络生成一张只有一个像素的图像，即采用 one-hot 的方式生成的位置。为了查看网络到底做了什么，我们可以放大目标像素周围的小区域。在图 5 中，目标像素以红色标出，我们展示了模型经过 SoftMax 激活与直接使用 Logits 作为预测的结果。第一个像素（顶行）是训练集中的结果，如预期那样模型有比较正确的预测，虽然在目标像素外还是存在一些概率。下一个像素（中间行偏右）在测试集中也是正确的，但因为目标的周围像素捕获了相差不大的概率，所以模型仅仅只是勉强正确。而最后的像素（底部偏右）则是完全错误的。这是非常令人惊讶的，因为作为 80/20 的分割结果，几乎所有测试像素都围绕着训练像素。

图 5：模型在较少相邻像素上的预测。网络出现了过拟合现象，即训练准确率非常完美，而测试准确率最高才 86%。这极为惊人，因为几乎所有测试像素都被训练像素所围绕。此外，网络很难拟合训练集，因为除目标像素外其它像素还存在着显著的概率。

第三个发现：监督回归对 CNN 来说也很难
那么，在给定位置的情况下，为什么高亮显示一个像素对网络来说如此困难？是因为将信息从一个小空间扩展到较大空间比较困难吗？在逆向任务上是否会容易一些？如果我们训练卷积网络来将图像信息压缩为标量坐标——更接近普通的图像分类，会怎样？结果发现，在监督回归任务上同样效果不佳.

看似简单的坐标转移任务在两类任务上展现卷积的问题：从笛卡尔（i, j）空间到 one-hot 像素空间以及反过来，即从 one-hot 像素空间至笛卡尔空间。即使在监督下训练，在只画一个像素的情况下，当训练样本均围绕测试样本时，卷积仍然无法学习笛卡尔空间和像素空间之间的平滑函数。并且，性能最好的卷积模型很大，充其量只能勉强工作，而且需要很长的时间来训练。

解决办法：CoordConv
卷积是等变的，意味着当每个滤波器被应用于输入以产生输出时，它并不知道每个滤波器的位置。我们可以通过让滤波器了解自己的位置来帮助卷积。为此，我们在输入中添加了两个通道——一个 i 坐标，一个 j 坐标。我们将由此产生的层称为 CoordConv，如下图所示：

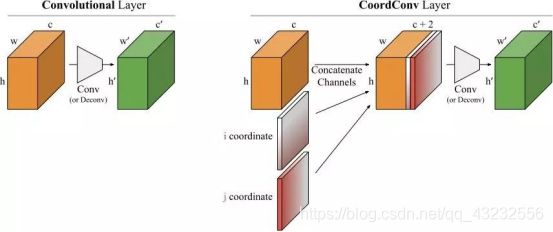
图 6：卷积层和 CoordConv 的对比。CoordConv 层将带有坐标信息的附加通道作为输入，此处指 i 坐标和 j 坐标。

提出的 CoordConv 层是对标准卷积层的简单扩展，其中卷积以坐标为条件。允许卷积滤波器观察到坐标会破坏平移等变性，这似乎是个坏主意。平移等变性不是卷积的标志性优势吗？我们认为，卷积获得成功的重要因素有三：使用的学习参数相对较少；在现代 GPU 上计算速度快；学习了平移等变性函数。CoordConv 层保留了前两个属性——参数较少和计算效率高，并且它的等变程度也可以学习。如果坐标中的权重学习为零，CoordConv 的表现将与标准卷积一样。另一方面，如果平移依赖对下游任务有用，那它也能学习这个。

CoordConv 解决之前的监督任务:如图 7、8 所示，CoordConv 模型在监督式坐标分类和监督式渲染任务的两种训练/测试分割中都具备完美的训练和测试性能。此外，CoordConv 模型的参数数量是性能最好的标准 CNN 参数数量的 1/100 - 1/10，且训练时间仅需数秒，比后者快 150 倍（标准 CNN 训练时间需要一个多小时）。

图 7：在监督式坐标分类任务上，CoordConv 在训练集和测试集上均可以快速获得完美的性能。

图 8：在监督式渲染任务中，很多 CoordConv 模型在训练集和测试集上均可以快速获得完美的性能。

为了进一步验证，图 9 展示了在绘制相邻像素时普通解卷积与 CoordConv 的性能对比。

图 9：如前所示，解卷积在监督式坐标分类任务上性能不好，而 CoordConv 获得了 100% 的训练和测试准确率。解决方案从视觉上看也简单得多。

在使用卷积来绘制像素时，我们观察到伪影和过拟合。而 CoordConv 在训练集和测试集上都取得了完美的性能。同样的事情还发生在相反的任务上。卷积在回归坐标时遇到困难，而 CoordConv 可以很好地建模函数，如图 10 所示：

图 10：卷积在建模监督式回归任务时遇到困难，而 CoordConv 可以实现很好的建模。

CoordConv 在多个领域中都能提供帮助
至此 Uber 展示了卷积网络在解决某类简单问题时的失败，并提出了 CoordConv 层形式的修正。很自然地，我们会想知道：该缺点仅存在于这个简单问题中吗？还是说这是一个在其它任务中隐匿存在的核心问题，并阻碍了性能优化？uber将CoordConv层嵌入多种任务的网络架构中训练。

其中在目标检测任务中，在一个简单的检测空白背景中零散 MNIST 数字的问题中，他们发现，使用 CoordConv 时 Faster R-CNN 的 IoU 提升了大约 24%。

在图像分类任务中，当添加一个 CoordConv 层到 ResNet-50 的底层并在 ImageNet 上训练时，我们发现仅有小量的提高。

在生成模型任务中，在诸如 GAN 和 VAE 的生成式模型中，像素是从隐参数空间中「画」出来的，在理想情况下或许能编码高级概念，例如位置。直观来说，CoordConv 也可能提供帮助。使用基于 Sort-of-CLEVR 形状的简单数据集，我们训练了 GAN 和 VAE 并展示了潜在空间之间的插值。

以一个简单的生成彩色形状的任务为例。插值的视频如图 11 所示，左边是普通的 GAN，右边是 CoordConv GAN，展示了 CoordConv 如何提升了生成模型的性能。

图 11：普通 GAN（左）和 CoordConv GAN（右）在潜在空间中的移动（插值）。

在生成模型中，我们在潜在空间的点之间使用插值，以探究 CoordConv 的影响，这是用于评估生成模型泛化能力的常用方法。

在普通的 GAN 中，我们观察到很明显的失真（就像黏在背景上），以及少量的目标伪影。通过 CoordConv GAN，目标变得连贯，并且移动变得更加平滑。训练 VAE 的时候也能发现类似的问题。通过卷积，我们发现图像中的目标部分出现了伪影，但利用 CoordConv，目标移动变得更加平滑。当使用更大型的 GAN 来生成大规模房间场景的场景理解（LSUN）时，通过卷积我们再次观察到了僵硬的目标伪影。加入 CoordConv 后，几何变换变得更加平滑，包括平移和变形。

在强化学习任务中，CoordConv 可能对其有所帮助。我们训练了一些智能体来玩 Atari 游戏，例如吃豆人。我们认为如果一个卷积滤波器能够同时识别吃豆人且提取她在迷宫中的位置，它就有助于学习更好的策略。

CNN 不能对坐标变换任务进行建模，且我们以 CoordConv 层的形式做了简单的修整。我们的结果表明，加入这些层后可以极大地提升网络在大量应用中的表现。未来研究将进一步评估 CoordConv 在大规模数据集中的优势，探索其在检测任务、语言任务、视频预测，以及配合空间 transformer 网络、前沿生成模型时的影响。