智能优化算法：回溯搜索优化算法-附代码

智能优化算法：回溯搜索优化算法

摘要：回溯搜索优化算法（BSA）是 Civicioglu于2013年提出 的 一种 基 于种群的元启发式算法。被广泛应用于寻优问题中，具有收敛速度快等特点。

1.算法原理

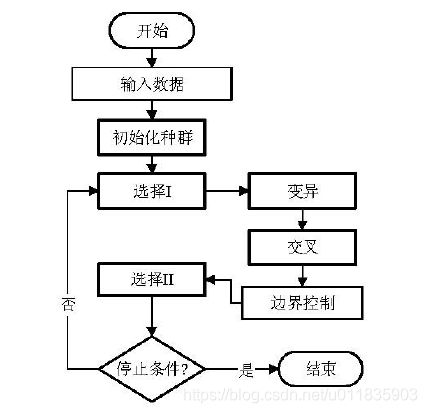
BSA是一种基于种群的新型启发式算法，与大多数元启发式算法类似，该算法通过种群的变异、交叉和选择来达到寻优的目的。BSA有着一个记忆种群的功能，该功能赋予了BSA一个强大的挖掘历史信息能力。BSA的繁殖算子即变异和交叉算子，作为自身算法的标志性特征，与其他进化算法有着本质的区别。BSA算法的基本流程图如图1所示，由5个步骤构成：初始化种群、选择Ｉ、变异、交叉和选择ＩＩ。每个步骤的具体内
容如下：

图1.BSA基本流程图

1.1 初始化种群

BSA 随机产生种群$P$ 和历史种群$oldP$，如式(1)所示:
$$P_{i,j}-U(lo{w}_j,u{p}_j),oldP-U(lo{w}_j,u{p}_j)\text{\hspace{1em}(1)}$$
式(1)中：$i\in [1,2,...,N],j\in [1,2,...,D]$，$N$和$D$分别代表种群 个 体 数 和 种 群 维 数；体数和种群维数；$lo{w}_j$和$u{p}_j$分别表示第$j$维分量的下界和上界；$U$为随机均匀分布函数。该步骤仅为算法提供随机的初始数据，不参与后面的迭代过程。

1.2 选择Ｉ

BSA的选择Ｉ过程是算法迭代起点。首先更新历史种群$oldP$，如(2)所示；再利用式(3)对其中个体位置进行随机排序。
$$ifa<b,thenoldP=P\text{\hspace{1em}(2)}$$

$$oldP=permuting(oldP)\text{\hspace{1em}(3)}$$

式(2)中：$a$与$b$是(0,1)中产生的两个均匀分布随机数。

该步骤相当于是以0.5的概率从前$n$代历史种群$oldP$和上代种群$P$中选出新的$oldP$，由此形成了独特的依概率记忆前代种群功能，这是算法能够进行“回溯”搜索的前提。该选择机制有一个特点：随着算法的迭代次数增多，选择前代历史种群$oldP$的概率会越来越小，而选择前代种群$P$的概率一直保持0.5不变，显然，选择前代种群$P$作为当代历史种群$oldP$的可能性更大。

1.3 变异

BSA采用式(4)对种群$P$进行扰动，得到变异种群$M$。
$$M=P+F\ast (oldP-P)\text{\hspace{1em}(4)}$$
式(4)中：$F$为变异控制参数,$F=3.randn$ ,$randn$是标准正态分布随机数。该过程从生物学角度看，表示当代种群$P$向前代种群$oldP$ 进行
学习，通过因子$F$加以控制，从而达到变异效果。该操作赋予了算法强大的全局搜索能力。

1.4 交叉

BSA的交叉过程较同类算法更为精密，可以分为两步。第一步，产生一个N*D大小的映射矩阵map，其初始元素值均为0，然后采用两种策略等概率更新映射矩阵map，如式(5)所示；第二步，根据生成的矩阵map确定种群P中交叉个体元素的位置，然后将P中的此类个体元素与种群M中对应位置元素进行互换，进而得到试验种群T，如式(6)或(7)所示。

简单来讲，该交叉过程由0-1矩阵map决定。当map中元素为1时，将M中对应元素赋给种群T；否则，将P中对应元素赋给种群T。
$$\{\begin{array}{l}ma{p}_{i,u(1,ceil(mixrate\ast rand\ast D))}=1,ifc<d\\ u=permuting(1,2,...,D)\\ ma{p}_{i,randi(D)}=0,else\end{array}\text{\hspace{1em}(5)}$$

$$T_{i,j}=\{\begin{array}{l}{M}_{i,j},ifma{p}_{i,j}=1\\ P_{i,j},else\end{array}\text{\hspace{1em}(6)}$$

$$T_{i,j}=P_{i,j}+ma{p}_{i,j}\ast F\ast (old{P}_{i,j}-P_{i,j})\text{\hspace{1em}(7)}$$

式(5)中：$c$和$d$为(0,1)上的均匀随机数；$ceil(.)$是向上取整函数；$rand(.)$为均匀分布的随机整数函数；$mixrate$表示交叉概率参数，在原始BSA中其值设置为１。式(6)和(7)在数学表达上不同，但具体交叉操作过程一致。式(6)偏向更直观理解交叉过程的原理，而式(7)则更清晰地描
述了试验种群$T$与种群$P$之间的关系。边界控制：交叉结束后，对试验种群$T$中个体进行边界控制，若$T$个体中存在越界元素，则这些元素均采用式(1)重新生成。

1.5 选择ＩＩ

BSA的选择ＩＩ过程由个体适应度决定。通过比较种群$P$和试验种群$T$ 中对应个体适应度值的大小，选择出具有更优适应度的个体，进而产
生新的种群$P$，如式（８）所示。
$$P_i=\{\begin{array}{l}{T}_i,fitness(T_i)<fitness(P_i)\\ P_i,else\end{array}\text{\hspace{1em}(8)}$$
BSA 利用选择ＩＩ这一步骤更新种群$P$，再回到选择Ｉ步骤参与下一次迭代，直至满足终止条件，输出最优解。

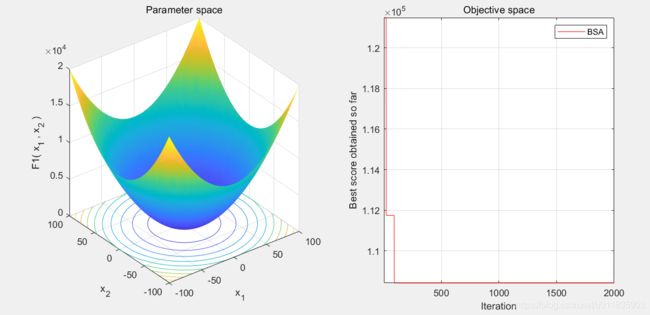
2.算法结果

3.参考文献

[1]王海龙,苏清华,胡中波.回溯搜索优化算法研究进展[J].湖北工程学院学报,2018,38(03):33-42.

4.Matlab代码

https://mianbaoduo.com/o/bread/aJaWk50=