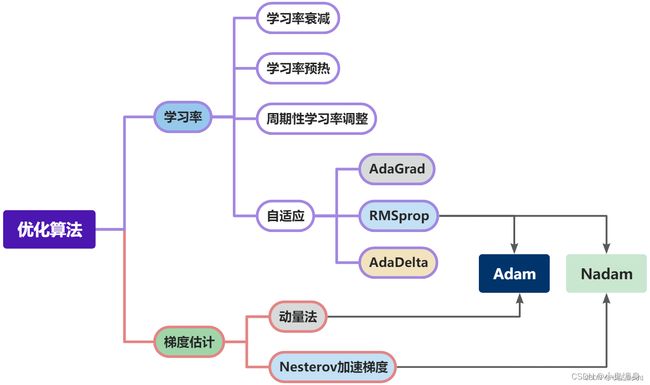
NNDL 作业11：优化算法比较

---

目录

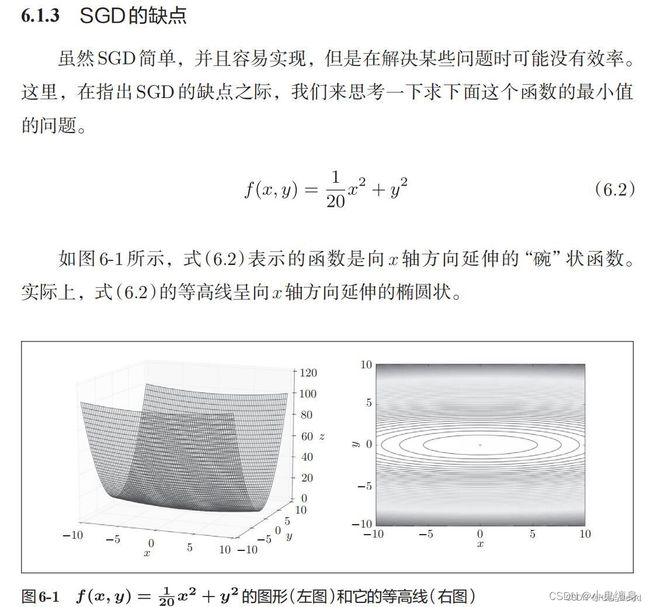
1. 编程实现图6-1，并观察特征

import numpy as np
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
 
 
# https://blog.csdn.net/weixin_39228381/article/details/108511882
 
def func(x, y):
    return x * x / 20 + y * y
 
 
def paint_loss_func():
    x = np.linspace(-50, 50, 100)  # x的绘制范围是-50到50，从改区间均匀取100个数
    y = np.linspace(-50, 50, 100)  # y的绘制范围是-50到50，从改区间均匀取100个数
 
    X, Y = np.meshgrid(x, y)
    Z = func(X, Y)
 
    fig = plt.figure()  # figsize=(10, 10))
    ax = Axes3D(fig)
    plt.xlabel('x')
    plt.ylabel('y')
 
    ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='rainbow')
    plt.show()
 
 
paint_loss_func()

2. 观察梯度方向

3. 编写代码实现算法，并可视化轨迹

SGD、Momentum、Adagrad、Adam

代码如下：

# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict
 
 
class SGD:
    """随机梯度下降法（Stochastic Gradient Descent）"""
 
    def __init__(self, lr=0.01):
        self.lr = lr
 
    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]
 
 
class Momentum:
    """Momentum SGD"""
 
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
 
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
            params[key] += self.v[key]
 
 
class Nesterov:
    """Nesterov's Accelerated Gradient (http://arxiv.org/abs/1212.0901)"""
 
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None
 
    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.v[key] *= self.momentum
            self.v[key] -= self.lr * grads[key]
            params[key] += self.momentum * self.momentum * self.v[key]
            params[key] -= (1 + self.momentum) * self.lr * grads[key]
 
 
class AdaGrad:
    """AdaGrad"""
 
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None
 
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
 
 
class RMSprop:
    """RMSprop"""
 
    def __init__(self, lr=0.01, decay_rate=0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None
 
    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)
 
        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
 
 
class Adam:
    """Adam (http://arxiv.org/abs/1412.6980v8)"""
 
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
 
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
 
        self.iter += 1
        lr_t = self.lr * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
 
        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key] ** 2 - self.v[key])
 
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
 
 
def f(x, y):
    return x ** 2 / 20.0 + y ** 2
 
 
def df(x, y):
    return x / 10.0, 2.0 * y
 
 
init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0
 
optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)
 
idx = 1
 
for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]
 
    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])
 
        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)
 
    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)
 
    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)
    # for simple contour line
    mask = Z > 7
    Z[mask] = 0
 
    # plot
    plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)  # 绘制等高线
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")
 
plt.subplots_adjust(wspace=0, hspace=0)  # 调整子图间距
plt.show()

4. 分析上图，说明原理（选做）

1. 为什么SGD会走“之字形”？其它算法为什么会比较平滑？
SGD算法是从样本中随机抽出一组，训练后按梯度更新一次，然后再抽取一组，再更新一次，在样本量及其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。SGD最有可能跳过局部最优解，但还有一种情况就是最陡的方向是全局最优解，而不陡的方向有局部最优解，而且曲线比较平缓，那么只要SGD随机到了不陡的方向，它也会陷入局部最优解。
其他算法比较平滑是因为对SGD梯度摆动的问题进行解决，从而得到的图像比较平滑。
2. Momentum、AdaGrad对SGD的改进体现在哪里？速度？方向？在图上有哪些体现？

[外链图片转存中…(img-6Qe0dCiC-1670060494535)]

Momentum:
为了消除梯度摆动带来的问题，可以知道梯度在过去的一段时间内的大致走向，以消除当前轮迭代梯度向量存在的方向抖动。改进：通过指数加权平均，纵向的分量基本可以抵消，原因是锯齿状存在一上一下的配对向量，方向基本反向。因为从长期的一段时间来看，梯度优化的大方向始终指向最小值，因此，横向的更新方向基本稳定。
这是老师讲的，可以解决SGD梯度摆动的缺点，速度较SGD快，能够跳出局部极小值。

AdaGrad:
Adagrad采用这是因为随着我们更新次数的增大，我们是希望我们的学习率越来越慢。因为我们认为在学习率的最初阶段，我们是距离损失函数最优解很远的，随着更新的次数的增多，我们认为越来越接近最优解，于是学习速率也随之变慢。所以图像比较平滑，最终收敛至最优点。

Adam:
Adam 是一种可以替代传统随机梯度下降过程的一阶优化算法，它能基于训练数据迭代地更新神经网络权重。主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳,从而图像比较平滑。

4. 仅从轨迹来看，Adam似乎不如AdaGrad效果好，是这样么？
   Adagrad采用的是学习率递减的办法，而Adam的学习采用的是一定范围内学习率的办法，两种存在差异，但是Adagrad要优于Adam下题6是解释在同种情况下的办法。

5. 四种方法分别用了多长时间？是否符合预期？
   SGD:0.21648932214740826
   Momentum:0.11593046640138721
   AdaGrad:0.033343153287890816
   Adam:0.039999528396092415
   可以看出SGD确实比较慢，而AdaGrad运行时间短于Adam所以AdaGrad的性能更好一些。

6. 调整学习率、动量等超参数，轨迹有哪些变化？
   学习率变小：
   

学习率同时扩大两倍的变化：

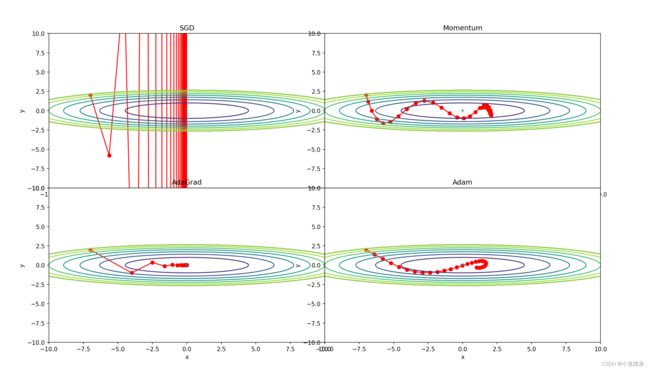
SGD:1 ;Momentum:1; AdaGrad:2;Adam:1

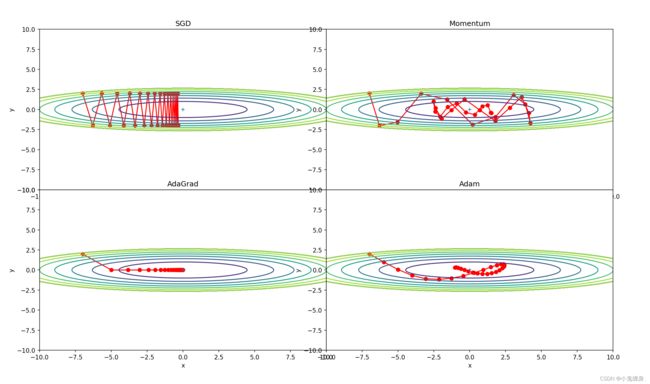
5. 总结SGD、Momentum、AdaGrad、Adam的优缺点（选做）

SGD:
优点：由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快。

缺点：SGD最大的缺点是下降速度慢,通常训练时间更长,而且可能会在沟壑的两边持续震荡,停留在一个局部最优点。

Momentum:
优点：加入的这一项，可以使得梯度方向不变的维度上速度变快，梯度方向有所改变的维度上的更新速度变慢，这样就可以加快收敛并减小震荡。
缺点：这种情况相当于小球从山上滚下来时是在盲目地沿着坡滚，如果它能具备一些先知，例如快要到坡底时，就知道需要减速了的话，适应性会更好。
Adagrad:
优点：能够放大梯度和约束梯度也适合处理稀疏梯度
缺点：仍依赖于人工设置一个全局学习率，设置过大的话，会使分母过于敏感，对梯度的调节太大，在中后期，分母上梯度平方的累加将会越来越大，使 损失更快->0，使得训练提前结束
Adam:
实现简单，计算高效，对内存需求少，参数的更新不受梯度的伸缩变换影响，超参数具有很好的解释性，且通常无需调整或仅需很少的微调，更新的步长能够被限制在大致的范围内（初始学习率），能自然地实现步长退火过程（自动调整学习率），很适合应用于大规模的数据及参数的场景，适用于不稳定目标函数，适用于梯度稀疏或梯度存在很大噪声的问题
缺点：
虽然Adam算法目前成为主流的优化算法，不过在很多领域里通常比Momentum算法效果更差。

6. Adam这么好，SGD是不是就用不到了？（选做）

不是，在很多领域里（如计算机视觉的对象识别、NLP中的机器翻译）的最佳成果仍然是使用带动量（Momentum）的SGD来获取到的。在计算机视觉领域，SGD时至今日还是统治级的优化器。但是在自然语言处理（特别是用Transformer-based models）领域，Adam已经是最流行的优化器了。

7. 增加RMSprop、Nesterov算法。（选做）

Nesterov：

#nesterov momentum
def update_parameters_with_nesterov_momentum(parameters, grads, v, beta, learning_rate):
	"""
	Update parameters using Momentum
	Arguments:
	parameters -- python dictionary containing your parameters:
					parameters['W' + str(l)] = Wl
					parameters['b' + str(l)] = bl
	grads -- python dictionary containing your gradients for each parameters:
					grads['dW' + str(l)] = dWl
					grads['db' + str(l)] = dbl
	v -- python dictionary containing the current velocity:
					v['dW' + str(l)] = ...
					v['db' + str(l)] = ...
	beta -- the momentum hyperparameter, scalar
	learning_rate -- the learning rate, scalar
	Returns:
	parameters -- python dictionary containing your updated parameters
	v -- python dictionary containing your updated velocities
	'''
	VdW = beta * VdW - learning_rate * dW
	Vdb = beta * Vdb - learning_rate * db
	W = W + beta * VdW - learning_rate * dW
	b = b + beta * Vdb - learning_rate * db
	'''
	"""

	L = len(parameters) // 2  # number of layers in the neural networks

	# Momentum update for each parameter
	for l in range(L):
		# compute velocities
		v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] - learning_rate * grads['dW' + str(l + 1)]
		v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] - learning_rate * grads['db' + str(l + 1)]
		# update parameters
		parameters["W" + str(l + 1)] += beta * v["dW" + str(l + 1)]- learning_rate * grads['dW' + str(l + 1)]
		parameters["b" + str(l + 1)] += beta * v["db" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]

	return parameters

RMSprop：

#RMSprop
def update_parameters_with_rmsprop(parameters, grads, s, beta = 0.9, learning_rate = 0.01, epsilon = 1e-6):
	"""
	Update parameters using Momentum
	Arguments:
	parameters -- python dictionary containing your parameters:
					parameters['W' + str(l)] = Wl
					parameters['b' + str(l)] = bl
	grads -- python dictionary containing your gradients for each parameters:
					grads['dW' + str(l)] = dWl
					grads['db' + str(l)] = dbl
	s -- python dictionary containing the current velocity:
					v['dW' + str(l)] = ...
					v['db' + str(l)] = ...
	beta -- the momentum hyperparameter, scalar
	learning_rate -- the learning rate, scalar
	Returns:
	parameters -- python dictionary containing your updated parameters
	'''
	SdW = beta * SdW + (1-beta) * (dW)^2
	sdb = beta * Sdb + (1-beta) * (db)^2
	W = W - learning_rate * dW/sqrt(SdW + epsilon)
	b = b - learning_rate * db/sqrt(Sdb + epsilon)
	'''
	"""
	L = len(parameters) // 2  # number of layers in the neural networks
	# rmsprop update for each parameter
	for l in range(L):
		# compute velocities
		s["dW" + str(l + 1)] = beta * s["dW" + str(l + 1)] + (1 - beta) * grads['dW' + str(l + 1)]**2
		s["db" + str(l + 1)] = beta * s["db" + str(l + 1)] + (1 - beta) * grads['db' + str(l + 1)]**2
		# update parameters
		parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads['dW' + str(l + 1)] / np.sqrt(s["dW" + str(l + 1)] + epsilon)
		parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads['db' + str(l + 1)] / np.sqrt(s["db" + str(l + 1)] + epsilon)

	return parameters

nesterov momentum表现：

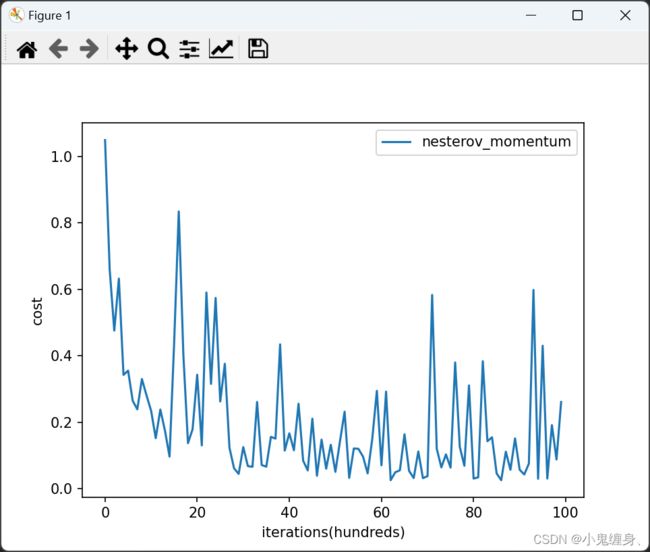
准确率：0.9210526315789473
RMSprop表现：

准确率：0.9473684210526316

8. 基于MNIST数据集的更新方法的比较（选做）

# coding: utf-8
# OptimizerCompare.py

import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from MultiLayerNet import MultiLayerNet
from util import smooth_curve
from optimizer import *


# 0:读入MNIST数据==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000

# 1:进行实验的设置==========
optimizers = {}
optimizers['SGD'] = SGD()
optimizers['Momentum'] = Momentum()
optimizers['AdaGrad'] = AdaGrad()
optimizers['Adam'] = Adam()
# optimizers['RMSprop'] = RMSprop()

networks = {}
train_loss = {}
for key in optimizers.keys():
    networks[key] = MultiLayerNet(
        input_size=784, hidden_size_list=[100, 100, 100, 100],
        output_size=10)
    train_loss[key] = []

# 2:开始训练==========
for i in range(max_iterations):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    for key in optimizers.keys():
        grads = networks[key].gradient(x_batch, t_batch)
        optimizers[key].update(networks[key].params, grads)

        loss = networks[key].loss(x_batch, t_batch)
        train_loss[key].append(loss)

    if i % 100 == 0:
        print("===========" + "iteration:" + str(i) + "===========")
        for key in optimizers.keys():
            loss = networks[key].loss(x_batch, t_batch)
            print(key + ":" + str(loss))

# 3.绘制图形==========
markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"}
x = np.arange(max_iterations)
for key in optimizers.keys():
    plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], \
    markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 1)
plt.legend()
plt.show()

结果：
=iteration:1200=
SGD:0.2986528195291609
Momentum:0.1037981040196782
AdaGrad:0.0668137679448615
Adam:0.05010293181776089
=iteration:1300=
SGD:0.17833478097202
Momentum:0.06128433751079029
AdaGrad:0.01779291355463178
Adam:0.036788168826807605
=iteration:1400=
SGD:0.30288604165486865
Momentum:0.07708723420976107
AdaGrad:0.036239187352732696
Adam:0.03584596636673899
=iteration:1500=
SGD:0.21648932214740826
Momentum:0.11593046640138721
AdaGrad:0.033343153287890816
Adam:0.039999528396092415
=iteration:1600=
SGD:0.23519516569365168
Momentum:0.06509188355944322
AdaGrad:0.0377409654184555
Adam:0.05803067028715449
=iteration:1700=
SGD:0.28851197390150085
Momentum:0.14561108131745754
AdaGrad:0.07160438141432544
Adam:0.07280250583341145
=iteration:1800=
SGD:0.14382629146685216
Momentum:0.03977221072571262
AdaGrad:0.015159891599626725
Adam:0.019623602905335474
=iteration:1900=
SGD:0.19067465612724083
Momentum:0.053986168113818435
AdaGrad:0.03665586658910679
Adam:0.038508895473566646

---

总结

本次实验通过对四种优化算法的比较和优缺点的思考，更加明白了每个优化器内在的原理和优化的方法。对于理解各类优化器有很大的帮助。同时查阅了很多大佬的博客，写这方面的很多，好的不少，对于他们的一些关于优化器的一些观点我也看了不少，感觉还是得亲身实践一番。

References:

NN学习技巧之参数最优化的四种方法对比（SGD, Momentum, AdaGrad, Adam）,基于MNIST数据集
Pytorch实现MNIST（附SGD、Adam、AdaBound不同优化器下的训练比较）
SGD有多种改进的形式，为什么大多数论文中仍然用SGD？
深度学习_深度学习基础知识_Adam优化器详解
通俗理解 Adam 优化器
梯度下降：BGD、SGD、mini-batch GD介绍及其优缺点
老师的博客：
NNDL 作业11：优化算法比较
如果还有大神的博客我采用到却没有粘上去，请联系我删除或者添加References,谢谢各位大神的博客，给了很多启发。