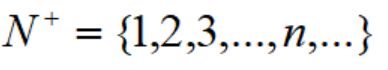集合概论

1.集合是具有某种特定性质，具体的或抽象的对象汇集的总体

2.集合的表示有枚举法和描述法

3.集合有三个性质——确定性，无序性，互异性

4.集合S的所有元素都属于集合T，称S是T的子集

5.如果S是T的子集，T中存在至少一个元素不属于S，称S是T的真子集

6.空集是一个元素都没有的集合，它是所有集合的子集，是所有非空集合的真子集

7.区间一般是实数的子集

8.集合的运算有四种——并、交、差、补

9.集合运算满足交换律、结合律、分配律和对偶律

10.由n个非负整数的元素构成的集合称为有限集，不是有限集的集合称为无限集

11.若无限集的元素可按某种规则排成一列，则称该集合是可列集

12.任一无限集包含可列子集，无限集不一定是可列集

13.可列个可列集之并也是可列集

14.有理数集合Q是可列集

从今天开始，我们正式进入数学基础第一个模块——数学分析的学习，从【集合论】开始吧，废话不多说，进入正题。

集合的定义与表示

• 集合的定义
  

集合是具有某种特定性质，具体的或抽象的对象汇集的总体

在集合的定义中，其中“对象”一般称为元素。我们约定，集合用大写表示，比如A,S,T；元素用小写表示，比如a,x,b。

数学上常见的集合用固定的记号表示：

• 集合的表示

集合的表示有两种方式，第一种是枚举法，就是把所有元素列举出来。

比如说光的基色的集合，可以表示为{红，绿，蓝}；

再比如正整数的集合，用枚举法表示为：

集合表示的第二种是描述法，它是指具有某种性质的元素的集合。

比如有理数集合Q用描述法表示为：

最后来介绍一下空集的概念。空集，顾名思义，是指没有一个元素的集合，用∅来表示：

集合的性质

• 集合性质
  

集合的性质有三个——元素唯一确定，元素之间无次序关系，重复元素没有意义。

集合的第一个性质也被称为确定性，它是指元素唯一确定，即给定一个集合和一个元素，该元素要么属于该集合，要么不属于该集合。

集合的第二个性质也被称为无序性，它是说任意两个集合的元素仅排列方式不同，那么这两个集合相同。比如

集合的第二个性质也被称为互异性，它是说一个集合的相同元素只出现一次。比如

子集与真子集

• 定义
  

对于集合S、T，若S的所有元素都属于T，则称S是T的子集

若S是T的子集，我们记作(有些书本记号可能不尽相同,阅读文献时注意区别)：

很显然，下面的关系成立：

我们可以把子集的关系用数学语言表述：

符号“⇒”表示蕴含的意思。

相对的，我们可以定义非子集：

对于集合S、T，若S中至少有一个元素不属于T，则不S是T的子集

若S不是T的子集，我们记作：

注：S不是T的子集，并非意味着S的所有元素都不属于T.

进一步，我们可以定义真子集：

若S是T的子集，在T中存在一个元素x不属于S，则称S是T的真子集

若S是T的真子集，我们记为：

这里要提一下空集∅，空集表示一个元素也没有。对于一个非空集合T，那么任意一个不属于T的元素，也就不属于∅。即命题

成立，其逆否命题也成立，也即：

所以，空集∅是任意集合的子集。

进一步，给定一个非空集合，存在一个元素属于该集合而不属于空集，因此，空集∅是任一非空集合的真子集.

比如对于集合T={a，b，c}，它的子集一共8个：

简便计算公式是2的n次方(n是集合元素个数)。

我们常见的区间一般是实数的子集。比如开区间(a,b)：

有了子集的概念，我们可以得到证明两个集合相同的方法。先看集合相同的定义：

若S与T的所有元素完全相同，则称两集合相同，记为S=T

两个集合相同，那么其互为子集，即：

注：“⇔ ”符号表示等价、相互蕴含、当且仅当的意思.

要证明两个集合相同，可以证明其互为子集即可。

集合的运算

集合的基本运算有四种——并、交、差、补

• 并集与交集
  

集合S与T的并集，指属于S或属于T的元素的集合，用记号∪表示；

集合S与T的交集，指属于S且属于T的元素的集合，用记号∩表示.

用数学表述为：

并集与交集满足以下三个定律。

• 交换律

• 结合律

• 分配律

这三条定律都是可以证明的，我们选择分配律的第二条来证明。要证明两个集合相等，只需要证明互为子集。分两步走。

第一步：

第二步：

至此，命题得证.

• 差集与补集

集合S与T的差集，是指属于S但不属于T的元素的集合,记为S\T或S-T；

设在集合X中讨论问题，S是X的子集。S关于X的补集是指，属于X但不属于S的元素的集合.

若T是S关于X的补集，则记：

根据定义，我们可以推出：

集合的运算还有一个对偶律，也称德摩根公式(De Morgan公式)：

无限集与可列集

定义：

若集合S由n个元素组成(n是非负整数),则称S是有限集.不是有限集的集合称为无限集；

如果无限集中的元素可按某种规则排成一列，则称该集合为可列集

由定义可知，有限集的元素个数一定是有限个，也就是可数的。无限集的元素无穷多个.

对于可列集，往往可以写成如下形式：

比如整数集合N+就是一个可列集，再比如满足sinx=0的x取值也构成一个可列集：

关于无限集与可列集，有如下命题成立：

• 任一无限集包含可列子集

• 无限集不一定是可列集合

比如实数集合R是无限集，但不是可列集(收敛准则第五条，这个以后证明)。

再比如整数集合Z是可列集。我们证明这一点，取

对于可列集，我们有如下定理。

定理1：可列个可列集之并也是可列集

证明这个定理的核心是这些可列集合的并集可以排成一列，并且保证元素既不重复也不遗漏。我们证明这一点。

设每个可列集排列规则如下：

它们的并集按照如下规则排列(康托尔对角线法)：

这样排列保证了元素不遗漏，其次遇到重复元素删除即可，这就证明了可列个可列集的并集依然是一个可列集。

根据这个定理可以得到第二个定理：

定理2：有理数集合Q是可列集

证明的关键是所有的有理数排成一列：

笛卡尔集合

定义：

特别的：