全连接神经网络的优化
全连接神经网络的优化
- 前言
- 1. 梯度消失
- 2. 梯度爆炸
-
- 2.1 固定阈值裁剪
- 2.2 根据参数的范数来衡量
- 3. 损失函数
-
- 3.1 Softmax
- 3.2 交叉熵损失
- 3.3 交叉熵损失和多类支撑向量机损失
- 4. 梯度下降优化
-
- 4.1 动量法
- 4.2 自适应梯度法
- 4.3 Adam
- 5. 批归一化
- 6. 过拟合与欠拟合
- 7. 应对过拟合
-
- 7.1 L2正则化
- 7.2 权重衰退
- 7.3 随机失活(丢弃法)
前言
从概念到不同层次了解全连接网络之后,最终需要通过神经网络对我们输入的数据进行若干次训练得到理想的结果。在训练过程中非线性因素:使激活函数去积分化、去微分化、梯度消失和梯度爆炸;批归一化、损失函数选择、过拟合与Dropout、模型正则等的问题都是需要不断优化和不断探测,本文将对其这些点进行总结。

1. 梯度消失
梯度消失:由于反向传播时,梯度是相乘的,如果局部梯度过小,在反向传播中,即造成梯度消失的问题,最终导致更新不到 W W W,即每次更新梯度之后,初始权值基本不变。
对于梯度消失问题激活函数该如何选择?
①Sigmoid激活函数的导数最大值为0.25,数值非常小,假设隐层有100层,Sigmoid的求导结果全都为0.1,则梯度反向传播时,会是0.1的100次方,使得梯度越向前传会越小,接近于0。同样地,tanh激活函数存在同样的问题,只是tanh激活函数收敛速度要比sigmoid快而已。
②ReLu函数在大于0的时候斜率为1,解决了梯度消关的问题,因为1的k次幂依然是1,但是小于0时,斜率变为0,此时更新权重时,停止更新。
小于0停止更新
优点:提供单侧抑制能力因为神经网络是全连接具有过拟合问题、停止更新的连接可缓解过拟合问题。
缺点:该神经元的信息已经不能进行传递,因为此时W已变为固定值导致神经元死亡,丢掉一些链接。
③Leaky ReLu:在小于0时,会继续更新权重,但是在0点不连续,因为0点没有导数值。
2. 梯度爆炸
梯度爆炸是由于链式法则的乘法特性导致的。
梯度爆炸:断崖处梯度乘以学习率后,会是一个非常大得值,从而“飞”出了合理区域,最终导致算法不收敛。

解决方案:
1.将学习率值设置小一点。
2.梯度裁剪。
2.1 固定阈值裁剪
设定阈值,当梯度小于/大于阈值时,更新的梯度为阈值。如图所示:

但是很难找到合适的阈值
2.2 根据参数的范数来衡量
对梯度的L2范数进行裁剪,也就是所有参数偏导数的平方和再开方。

3. 损失函数
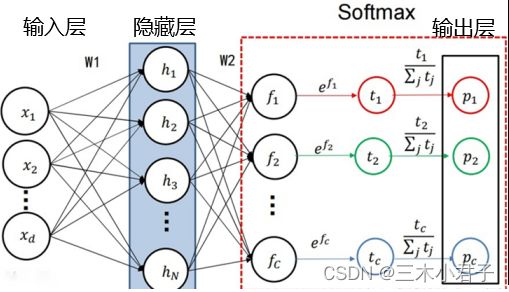
3.1 Softmax
Softmax是先对每个类别的得分进行 e e e指数函数变换,然后进行归一化处理(每个类别的得分除以所有类别的得分总和),最终输出每个类别的概率值。
3.2 交叉熵损失
熵的概念:简单理解就是反映信息量的多少,当某一个事件很确定时,表示无信息量,当事件的每种可能性概率值相等时,此时熵是最大的。

如何衡量两个随机分布的差异?
只有真实的分布为one-hot形式时,交叉熵和相对熵是相等的,但是当真实分布不为one-hot形式的时候,此时应该选择相对熵来比较两者之间的差异。
3.3 交叉熵损失和多类支撑向量机损失
①计算逻辑的不同,多类支撑向量机损失关注正确类别的分数是不是比其他每个类别的分数都高于1,而交叉熵损失是度量的每个类别概率值与真实值之间的差异。
②交叉熵损失要求真实类别的分数不仅比其他类别大,还要求真实类别的概率也比其他类别要大。
4. 梯度下降优化
4.1 动量法

动量法通过累加速度,减少震荡,也具有寻找更优的解:
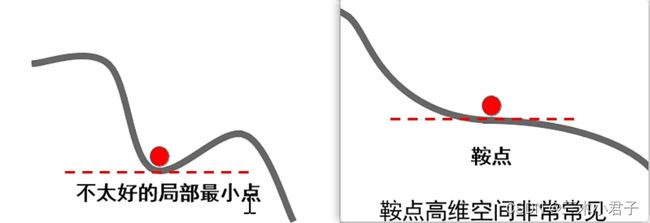
现象:损失函数常具有不太好的局部最小值或鞍点
梯度下降算法存在的问题:局部最小处与鞍点处梯度为0,算法无法通过。
动量法优势:由于动量的存在,算法可以冲出局部最小点以及鞍点,找到更优的解。
4.2 自适应梯度法
自适应梯度法通过减小震荡方向步长,增大平坦方向步长来减小震荡,加速通往谷底方向。
如何区分震荡方向与平坦方向?
答:梯度幅度的平方较大的方向是震荡方向;梯度幅度的平方较小的方向是平坦方向。

但是AdaGrad有一个缺点, r r r值会随着迭代次数的增多导致步长会很小,以致走不动,失去了调节的意义。RMSProp方法,在AdaGrad进行了改进,在梯度上乘了一个小于1的系数。

4.3 Adam
同时使用动量与自适应梯度思想,修正偏差步骤可以极大缓解算法初期的冷启动问题。
当刚开始更新权值时,如果直接使用 v v v,则步长为0.1 g g g,步长太小,权值更新慢,如果使用修正之后的 v ~ \tilde v v~,则步长为1 g g g。当迭代10次以上时, u u u的 t t t次方会很小,就会失去作用,此时修正后的 v ~ \tilde v v~约等于 v v v。

5. 批归一化
6. 过拟合与欠拟合
过拟合:是指学习时选择的模型所包含的参数过多,以至于出现这一模型对已知数据预测的很好,但对未知数据预测得很差的现象。这种情况下模型可能只是记住了训练集数据,而不是学习到了数据特征。
欠拟合:模型描述能力太弱,以至于不能很好地学习到数据中的规律。产生欠拟合的原因通常是模型过于简单。
7. 应对过拟合
最优方案——获取更多的训练数据。
次优方案——调节模型允许存储的信息量或者对模型允许存储的信息加以约束,该类方法称为正则化。
7.1 L2正则化
L2正则化使得模型分界面更加平滑,不会生成更复杂的的分界面。

7.2 权重衰退
通过限制参数值的范围来到达缩小模型容量的目的。

θ \theta θ越小正则项越小
使用拉格朗日乘子法求解,那么构造:

而对于 λ \lambda λ和 θ \theta θ知其—就可以解出另一个,所以可以等价为:
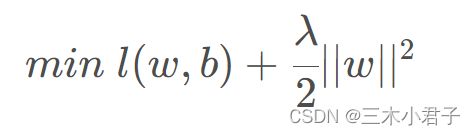
即 λ → ∞ \lambda \to \infty λ→∞, w ∗ → 0 w^* \to 0 w∗→0使用 λ \lambda λ来控制 θ \theta θ
那么梯度的计算和参数更新就变为:


当 λ η < 1 \lambda \eta < 1 λη<1时,实现了权重衰退
7.3 随机失活(丢弃法)
随机失活:让隐层的神经元以一定的概率不被激活。
实现方式:训练过程中,对某一层使用Dropout,就是随机将该层的一些输出舍弃(输出值设置为0),这些被舍弃的神经元就好像被网络删除了一样。
随机失活比率(Dropout ratio):是被设为0的特征所占的比例,通常在0.2~0.5范围内。
Dropout只在训练时启用,用于调整参数,在推理时并不使用。
随机失活为什么能够防止过拟合呢?
①随机失活使得每次更新梯度时参与计算的网络参数减少了,降低了模型容量,所以能防止过拟合。
②随机失活鼓励权重分散,即起到正则化的作用,进而防止过拟合。
③随机失活,也相当于模型集成,模型集成一般都会提高精度,防止过拟合。
以上是对全连接神经网络中存在需要优化点的分享,照片资料来源于北京邮电大学 鲁鹏老师 计算机视觉与深度学习。
