两层及N层全连接神经网络模型原理
两层及N层全连接神经网络模型原理
- 前言
- 1. 两层MLP
-
- 1.1 前向传播
- 1.2 反向传播
- 2. N层MLP
-
- 2.1 网络参数
- 2.2 超参数优化
- 3. MLP优化
前言
深度学习是学习样本数据的内在规律和表示层次,在学习过程中获得的信息对诸如文字,图像和声音等数据的解释有很大的帮助。全连接神经网络(MLP)便是基础的网络类型的之一,充分体现深度学习方法相比于传统机器学习算法的特点,即大数据驱动、公式推导、自我迭代更新、黑匣子训练等。本文将对MLP从两层及以上对其分析和解释。
1. 两层MLP
两(浅)层神经网络相比单层网络的差别在于隐藏层有多个神经节点,这就使得其可以处理“多输入多输出”的复杂问题。
1.1 前向传播
y ( x , W ) = W x + b {\rm{y}}(x,W) = Wx + b y(x,W)=Wx+b
其中, x x x代表输入图像,其维度为 d d d; y y y为分数向量,其维度等于类别个数 c c c; W = [ w 1 ⋅ ⋅ ⋅ w c ] T W = [w_1 \cdot \cdot \cdot w_c ]^T W=[w1⋅⋅⋅wc]T为权值矩阵, w i = [ w i ⋅ ⋅ ⋅ w i d ] T w_i = [w_i \cdot \cdot \cdot w_{id} ]^T wi=[wi⋅⋅⋅wid]T为第 i i i个类别的权值向量; b = [ b i ⋅ ⋅ ⋅ b c ] T b = [b_i \cdot \cdot \cdot b_c ]^T b=[bi⋅⋅⋅bc]T为偏置向量, b i b_i bi为第 i i i个类别的偏置,则两层MLP为
y = W 2 σ ( 0 , W 1 x + b 1 ) + b 2 y = W_2 \sigma (0,W_1 x + b_1 ) + b_2 y=W2σ(0,W1x+b1)+b2,其中 σ \sigma σ为激活函数
1.2 反向传播
反向传播所做的就是让每一个神经元都拥有一个 W 和 b W和b W和b的值,即求梯度。这样我们在传进一个新的数据时,我们可以对它准确的预测,当然也是对每一层传播来的数据的反馈。当对数据进行反馈时,损失函数是便是评测手段,下面将以均方差损失函数为例对其梯度下降。
损失函数: L ( y ^ , y ) = 1 2 ( y ^ i − y i ) 2 L(\hat y,y) = \frac{1}{2}(\hat y_i - y_i )^2 L(y^,y)=21(y^i−yi)2
梯度下降: w 1 = w 0 − η d L ( w ) d w b 1 = b 0 − η d L ( b ) d b \begin{array}{l}w_1 = w_0 - \eta \frac{{dL(w)}}{{dw}} \\ \\ b_1 = b_0 - \eta \frac{{dL(b)}}{{db}}\\ \end{array} w1=w0−ηdwdL(w)b1=b0−ηdbdL(b)
其中 w 0 w_0 w0和 b 0 b_0 b0是我们目前的实际值, − η - \eta −η是步长(一定的值),当 L L L取极值 w w w时, w 1 w_1 w1是梯度下降求出的值
当对损失函数梯度下降时需要链式法则求解
d L ( a , y ) d w = d L ( a , y ) d a ⋅ d a d z ⋅ d z d w \frac{{dL(a,y)}}{{dw}} = \frac{{dL(a,y)}}{{da}} \cdot \frac{{da}}{{dz}} \cdot \frac{{dz}}{{dw}} dwdL(a,y)=dadL(a,y)⋅dzda⋅dwdz
推演:
梯度下降带入损失函数
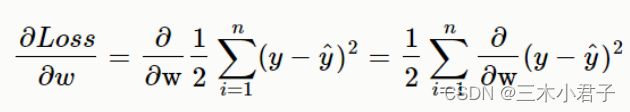
链式法则
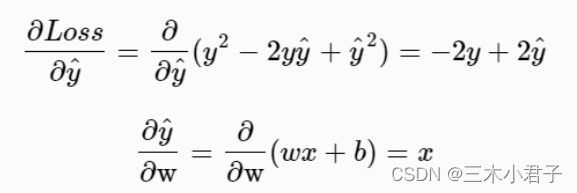
最终结果

2. N层MLP
N层全连接神经网络——除输入层之外其他层的数量为N的网络。
在神经网络中,随着网络的层数增加,每一层对于前一层次的抽象表示更深入。每一层神经元学习到的是前一层神经元值的更抽象的表示。三层神经网络也叫两隐藏层神经网络,则三层MLP为: y = W 3 σ ( 0 , W 2 σ ( 0 , W 1 x + b 1 ) + b 2 ) y = W_3 \sigma (0,W_2 \sigma (0,W_1 x + b_1 ) + b_2 ) y=W3σ(0,W2σ(0,W1x+b1)+b2) ,其中 σ \sigma σ为激活函数。
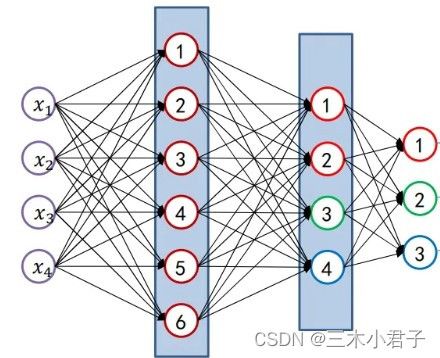
2.1 网络参数
参数:指算法运行迭代、修正最终稳定的值。
超参:网络结构——隐层神经元个数,网络层数,非线性单元选择等
优化相关——学习率、dropout比率、正则项强度等
2.2 超参数优化
网格搜索法:
①每个超参数分别取几个值,组合这些超参数值,形成多组超参数;
②在验证集上评估每组超参数的模型性能;
③选择性能最优的模型所采用的那组值作为最终的超参数的值。
随机搜索法:
①参数空间内随机取点,每个点对应一组超参数;
②在验证集上评估每组超参数的模型性能;
③选择性能最优的模型所采用的那组值作为最最终的超参数的值。
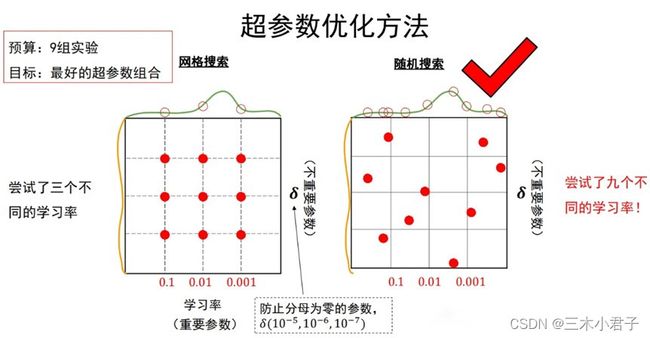
超参数搜索策略:
①粗搜索:利用随机法在较大范围里采样超参数,训练一个周期,依据验证集正确率缩小超参数范围。
②精搜索:利用随机法在前述缩小的范围内采样超参数,运行模型五到十个周期,选择验证集上精度最高的那组超参数。

3. MLP优化
非线性因素:围绕激活函数,提高计算速率就要使激活函数去积分化、去微分化、易求偏导,解决梯度消失和梯度爆炸的问题;
迭代更新:围绕反向传播更新权值和偏置,损失函数选择、优化器选择、学习率衰减策略等;
骨干网络:网络应该设置多少层,每一层应该有多少个节点。
以上是两层及N层(以三层举例)的MLP模型原理,对于MLP优化您可以查阅本栏目全连接神经网络的优化与改进。