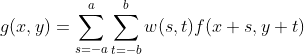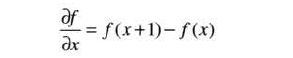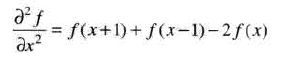数字图像处理第三章——灰度变换与空间滤波

目录

引言：

一、相关背景

1.1 灰度变换与空间滤波基础

二、基本灰度变换函数

2.1 图像反转

2.2 对数变换

2.3 幂律（伽马）变换

2.4 分段线性变换函数

 三、直方图处理

3.1 直方图均衡

3.2 直方图匹配（规定化）

四、空间滤波

4.1 机理

4.2 相关与卷积

五、平滑空间滤波器

5.1 平滑线性滤波器

5.2 统计排序（非线性滤波）滤波器

 六、锐化空间滤波器

6.1 拉普拉斯算子（处理二阶微分）

6.2 soble算子（处理一阶微分）

---

引言：

本章将重点对灰度变换与空间滤波进行了解。灰度变换是作用于图像的单个像素的，主要以对比度和阈值处理为目的，而空间滤波则涉及改善性能的操作，包括利用图像中每个像素的邻域处理来锐化图像。

一、相关背景

1.1 灰度变换与空间滤波基础

        空间域处理可由：g(x,y) = T[f(x,y)]表示，其中 f(x,y)是输入图像，g(x,y)为经过处理后的图像，T 则为一种算子定义在f上。这种算子可以应用在单幅图像或图像集合上。

        上图展示了单幅图像通过g(x,y) = T[f(x,y)]进行处理，邻域原点从一个像素向另一个像素移动，并对邻域中的像素应用算子T，在该位置产生输出。我们不妨假设一下，将T定义为“计算邻域的平均灰度”，当指定像素点位置为(100,150)时，以其为中心的8的相邻点之和除以9，就是我们所需要的结果，对应上述式子就是f(100，150)与它邻域的累加在T的作用下得到g(100,150)。而后原点移动到下一位置重复上述过程，就可以得到我们想要的结果。

上述过程称为空间滤波，邻域与预定义的操作一起称为空间滤波器（也称为空间掩模、核、模板或窗口）滤波器的的特性由邻域执行的操作决定。

        灰度变化函数:s = T(r)是当最小邻域为1*1的特殊情况下的函数，其中r，s分别表示变量，即g和f在任意点(x,y)处的灰度。

二、基本灰度变换函数

        上文中提到了灰度变换函数，r，s分别代表着处理前后的像素值，这里便介绍一下图像增强的三类基本函数：线性函数（反转函数和恒等变换）、对数函数（对数和反对数变换）、幂律函数（n次幂和n次根变换）。

2.1 图像反转

        与恒等变换不同的是反转变换可以得到灰度级范围为【0，L-1】的反转图像。

img = cv2.imread('D:\\picture\\tupian.jpg')
gray_image = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
height = gray_image.shape[0]
width = gray_image.shape[1]

result = np.zeros((height, width), np.uint8)
for i in range(height):
    for j in range(width):
        gray = 255 - int(gray_image[i, j])
        result[i, j] = np.uint8(gray)
cv2.imshow("gray image", gray_image)
cv2.imshow("result", result)

cv2.waitKey(0)
cv2.DestoryAllWindows()

2.2对数变换

        c为一个常数，且设r>=0.该变换将输入中范围较窄的低灰度值映射到输出中范围较宽范围的灰度值。同理，对于高的输入灰度值也是如此。

def log_plot(c):
    x = np.arange(0, 256, 0.01)
    y = c * np.log(1 + x)
    plt.plot(x, y, 'r', linewidth=1)
    plt.rcParams['font.sans-serif'] = ['simHei']
    plt.title(u'对数变换函数')
    plt.xlim(0, 255), plt.ylim(0, 255)
    plt.show()


def log(c, img):
    output = c *np.log(1.0 + img)
    output = np.uint8(output + 0.5)
    return output


img = cv2.imread('D:\\picture\\tupian.jpg')

log_plot(42)

result = log(42,img)

cv2.imshow("image", img)
cv2.imshow("result", result)

cv2.waitKey(0)
cv2.DestoryAllWindows()

2.3 幂律（伽马）变换

基本形式为：其中c和y均为正常数，当考虑到偏移量时（即输入为0时的一个可度量输出），也可将其写为。

def gama_plot(c, gama):
    x = np.arange(0, 256, 0.01)
    y = c * x ** gama
    y = c * np.power(x, gama)
    plt.plot(x, y, 'r', linewidth=1)
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.title(u'伽马变换')
    plt.xlim([0, 255]),plt.ylim([0, 255])
    plt.show()

def gama(img,c,gama):
    gama_table = c * [np.power(x / 255.0,gama) * 255.0 for x in range(256)]
    gama_table = np.round(np.array(gama_table)).astype(np.uint8)
    output = cv2.LUT(img, gama_table)
    return output


def gama_1(img, c, gama):
    output = c * np.power(img / float(np.max(img)), gama)*255.0
    output = np.uint8(output)
    return output


img = cv2.imread('D:\\picture\\tupian.jpg')
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
gama_plot(1, 4.0)
result1 = gama(gray, 1, 0.4)
result = gama_1(gray, 1, 0.6)

cv2.imshow("image", img)
cv2.imshow("result1", result)
cv2.imshow("result" , result1)

cv2.waitKey(0)
cv2.DestoryAllWindows()

        y值不同时，曲线也不同如下图所示。我们可以得到c=y=1时可简化为恒等变换。

2.4分段线性变换函数

对比度拉伸是最简单的分段线性函数，它是扩展图像灰度级动态范围的处理，因此，可以跨越记录介质和显示装置的全部灰度范围。

下面代码与图像展示了图像对比度增强的效果

img = cv2.imread('D:\\picture\\tupian.jpg')
gray_image = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
height = gray_image.shape[0]
width = gray_image.shape[1]

result = np.zeros((height, width), np.uint8)
for i in range(height):
    for j in range(width):
        if int(gray_image[i,j]*1.8)>255:
            gray = 255
        else:
            gray = int(gray_image[i,j]*1.8)
        result[i,j] = np.uint8(gray)
cv2.imshow("gray image", gray_image)
cv2.imshow("result", result)

cv2.waitKey(0)
cv2.DestoryAllWindows()

 三、直方图处理

        灰度级范围在【0，L-1】的数字图像的直方图是离散函数,其中是第k级灰度值，是图像中灰度为的像素个数。通常我们使用乘积MN表示图像像素的总数除以它的每个分量来归一化直方图。给出了归一化的直方图。从中我们可以知道，归一化直方图的所有分量之和等于1。

3.1直方图均衡

        我们知道灰度变换形式为：s = T(r)，，其中r=0表示黑色,r= L-1表示白色。

假设：（a）T(r)在区间上为单调递增函数

           （b）当时,

 通过python代码可得到它的直方图展示

def zhifang(img, type):
    color = (255, 255, 255)
    windowName = "gray"
    if type == 1:
        color = (255, 0, 0)
        windowName = 'blue'
    elif type == 2:
        color = (0, 255, 0)
        windowName = 'green'
    else:
        color = (0, 0, 255)
    hist = cv2.calcHist([img],[0],None,[256],[0,255])
    minV, maxV, minL, maxL = cv2.minMaxLoc(hist)
    histImg = np.zeros([256,256,3],np.uint8)

    for h in range(256):
        interNormal = int(hist[h] / maxV * 256)
        cv2.line(histImg, (h, 256),(h, 256 - interNormal), color)
    cv2.imshow(windowName, histImg)
    return histImg


img = cv2.imread('D:\\picture\\test.jpg')
channels = cv2.split(img)
for i in  range(3):
    zhifang(channels[i], 1+i)
cv2.waitKey(0)

 利用python中的cv2.equalizeHist()可以实现图像的均衡化。

img = cv2.imread('D:\\picture\\test.jpg')#插入图像
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)#彩色图像转为灰色
dat = cv2.equalizeHist(gray)#均衡化处理
cv2.imshow('gary', gray)#输出灰色图像
cv2.imshow('dat', dat)#输出均衡化图像
cv2.waitKey(0)

 3.2直方图匹配（规定化）

        直方图均衡能够自动 的确定变换函数，该函数寻求产生有均匀直方图的输出图像，当需要自动增强时，均衡化很有用，因为它的结果可通过计算得知，且容易实现。但对于图片处理后出现特殊情况的时候，就要使用另一种方法了，这种方法我们称为直方图匹配或规定化。

        我们令和分别表示它们所对应的连续概率密度函数，r和z表示输入图像和输出图像的灰度级。令s为一个有如下特性的随机变量：

 w为积分假变量，我们可以观察处这个表达式便是

 给出的直方图均衡的连续形式。

        重新定义一个具有如下特性的随机变量z：

 其中t为积分假变量。由两个等式可得T(r)=G(r)，为此z必须满足：

 由此，我们可以得知，若想将一幅给定图像转化为灰度级具有指定概率密度函数的图像，可由以下步骤实现：

  (1)由输人图像得到，并求得s的值。使用指定的 PDF求得变换函数G(z)。

  (2)求得反变换函数;因为z是由s得到的,所以该处理是s到z的映射,而后者正是我们期望的值。 

  (3)首先对输入图像进行均衡得到输出图像;该图像的像素值是s值。对均衡后的图像中具有s值的每个像素执行反映射，得到输出图像中的相应像素。当所有的像素都处理完后,输出图像的PDF将等于指定的PDF。

四、空间滤波

        空间滤波是图像处理领域应用广泛的主要工具之一，滤波一词借用与频域处理，例如低通滤波器的最终效果是模糊一幅图像，我们也可以通过空间滤波器直接作用于图像本身而完成类似的平滑。

4.1机理

        空间滤波器是由一个邻域和对该邻域包围的图像像素执行的预定义操作组成。滤波产生一个新的像素，新像素的坐标等于邻域中心的坐标，像素的值是滤波操作的结果。而滤波器的中心访问输入图像中的每个像素就生成了处理后的图像。

        滤波器又分为线性滤波器和非线性滤波器，由执行在像素上的操作决定。

        上图说明了使用3*3邻域的线性空间滤波的机理。在图像的任意一点（x，y），滤波器的响应g(x,y)是滤波器系数与该滤波器包围的像素的乘积的总和： 亦或者可以用下式表示,x和y是可变的，以便w中的每个像素可访问f中的每个像素。

 4.2相关与卷积

        相关是滤波器模板移过图像并计算每个位置乘积之和的处理。卷积与相关类似但滤波器在处理前首先需要翻转180度。现在将通过下图对其加以讲解：

        从图中我们可以看到滤波器w在与包含有全部0和单个1的函数相关下，得到的结果是w的一个拷贝，但与原本的值相比旋转了180度。在信号与系统分析中我们接触到单位冲激信号，我们就可以将其看成是一个离散的单位冲激。由此我们可以得出一个结论即：一个函数与离散单位冲激相关，得到的是该函数的翻转版本。

         而若想得到的函数与原本函数一致，我们需要预先将其旋转180度，之后再执行与相关一致的操作，这个操作就与卷积的概率不谋而合了，上图右侧的部分就显示了卷积后的结果。若将一维函数拓展到图像，则对于大小为n*m的滤波器，我们需要在顶部与底部填n-1行0，在左侧和右侧填充m-1行0。如下图所示，其执行步骤与一维函数类似。

五、平滑空间滤波器

        平滑滤波器用于模糊处理和降低噪声。通过线性滤波和非线性滤波模糊处理可达到降低噪声的结果。

5.1平滑线性滤波器

        平滑线性空间滤波器的输出(响应)是包含在滤波器模板邻域内的像素的简单平均值。一般称作均值滤波器，也可以将其归入低通滤波器。

        平滑滤波器是使用滤波器模块确定的邻域像素的平均灰度值代替图像中每个像素的值，使得图像灰度的“尖锐”变化得到降低。由于典型的随机噪声由灰度级的急剧变化组成，因此常见的平滑处理应用就是降低噪声。

         上图显示了两个3*3的平滑滤波器，第一个滤波器产生模块下方的标准像素平均值，把模块系数代入：

        上式的1/9仅在系数全为1是是这样，一个m*n模块应有等于1/mn的归一化常数。若所有系数都相等，则将该均值滤波器称为盒装滤波器。 第二个滤波器模块产生所谓的加权平均，即一些像素的权重比其他的要大一些。通常两种模板处理后的图像很难分辨是采用哪种模板处理的。

        下面就利用python实现一下均值滤波。

def avg_fliter(image):
    img = cv2.imread(image)
    rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
    result = cv2.blur(img, (6, 6))

    title = ['original image', 'blur image']
    images = [rgbimg, result]

    for i in range(2):
        plt.subplot(1, 2, i+1), plt.imshow(images[i])
        plt.title(title[i])
        plt.xticks([]),plt.yticks([])
    plt.show()


if __name__ == '__main__':
    image = 'D:\\picture\\test.jpg'
    avg_fliter(image)

 5.2统计排序（非线性滤波）滤波器

        统计排序滤波器是一种非线性空间滤波器，这种滤波器的响应以滤波器包围的图像区域中所包含的像素的排序(排队)为基础，然后使用统计排序结果决定的值代替中心像素的值。中值滤波器的使用非常普遍，这是因为对于一定类型的随机噪声，它提供了一种优秀的去噪能力，而且比相同尺寸的线性平滑滤波器的模糊程度明显要低.中值滤波器对处理脉冲噪声非常有效，该种噪声也称为椒盐噪声，因为这种噪声是以黑白点的形式叠加在图像上的。

def middle_filter(imagename):
    img = cv2.imread(imagename)
    rgbimg = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
    middle = cv2.medianBlur(img, 5)
    titles = ['origin image', 'result']
    images = [rgbimg,middle]
    for i in range(2):
        plt.subplot(1, 2, i+1), plt.imshow(images[i])
        plt.title(titles[i])
        plt.xticks([]),plt.yticks([])
    plt.show()

if __name__ == '__main__':
    imagename = 'D:\\picture\\test2.jpg'
    middle_filter(imagename)

 六、锐化空间滤波器

        锐化处理的主要目的是突出灰度的过渡部分，图像锐化的应用场景很多，从电子印刷和医学成像到工业检测和军事系统的制导等都有涉及。在上一节中我们了解到图像的模糊是用像素邻域平均法实现的，而均值处理与积分类似，因此在逻辑上我们可以得出锐化处理可由空间微分来实现这一结论。

        对于一维函数f(x)，其一阶微分的基本定义是差值

 对于二维函数，同样成立，我们便将二阶微分定义为：

        数字图像中的边缘在灰度上常常类似于斜坡过渡，这样就导致图像的一阶微分产生较粗的边缘，因为沿着斜坡的微分非零.另一方面，二阶微分产生由零分开的一个像素宽的双边缘.由此，我们得出结论，二阶微分在增强细节方面要比一阶微分好得多，这是一个适合锐化图像的理想特性.正像在本节稍后将要了解的那样，二阶微分比一阶微分执行上要容易得多，所以，我们开始主要注意二阶微分。

6.1 拉普拉斯算子（处理二阶微分）

一个二维图像的拉普拉斯算子定义为

 我们指导任意阶微分都是线性操作，所以拉普拉斯算子也是一个线性算子，为了以离散形式描述这一公式，在x方向上我们将其化为：

在y方向上我们也可以将其化为： 

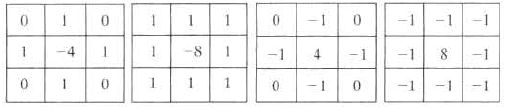
 在这三个公式下，两个离散的拉普拉斯算子可以写做

 图为常见拉普拉斯核

 用python实现拉普拉斯算子

plt.figure(figsize=(20,20))

img = cv2.imread('D:\\picture\\test2.jpg')
img1 = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)

result = cv2.Laplacian(gray, cv2.CV_16S, ksize=3)
la = cv2.convertScaleAbs(result)

plt.subplot(121),plt.imshow(img,'gray')
plt.subplot(122),plt.imshow(la,'gray')
plt.show()

 6.2 soble算子（处理一阶微分）

图像处理中一阶微分是用梯度幅值在实现的，对于函数f(x,y),f在坐标(x,y)处的梯度定义为二维列向量

这个向量指出了在位置(x,y)处f的最大变化率方向。其幅度值可由M(x,y)表示：

在某些情况下，用绝对值来近似平方和平方根操作更适合计算。

 python实现如下：

img = cv2.imread('D:\\picture\\test2.jpg')
x = cv2.Sobel(img[:, :, 0],cv2.CV_16S, 1, 0)
y = cv2.Sobel(img[:, :, 0],cv2.CV_16S, 0, 1)
absX = cv2.convertScaleAbs(x)
absY = cv2.convertScaleAbs(y)
res = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
cv2.imshow("result",res)
cv2.imshow("origin",img)
cv2.waitKey(0)