算法60天-Day24(回溯算法补充):剪枝到底剪了什么
 代码随想录(截图自参考【1】)
代码随想录(截图自参考【1】)
上篇文章中讲到回溯算法的本质就是暴力搜索,但是可以通过剪枝来进行优化。
那么,剪枝到底剪了什么?如何剪?
我们仍然以上篇文章的组合问题来进行讨论。
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。 你可以按 任何顺序 返回答案。
剪枝到底剪了什么
Carl师兄的网站上给出的剪枝优化的图如下:
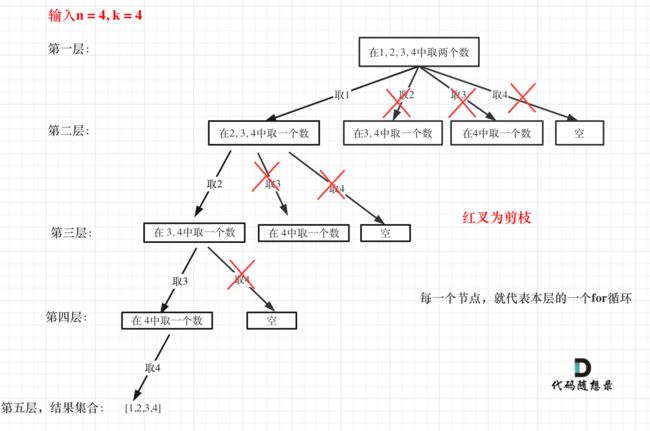 剪枝
剪枝
- 所谓的剪枝就是优化每一层的for循环。
不剪枝
为了对比,我们先查看原始的回溯算法输出:
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res = []
path = []
def backtrack(n, k, StartIndex):
if len(path) == k:
res.append(path[:])
return
for i in range(StartIndex, n + 1):
print(i) # 用于查看中间输出
path.append(i)
backtrack(n, k, i+1)
path.pop()
backtrack(n, k, 1)
return res
中间输出是这样子:
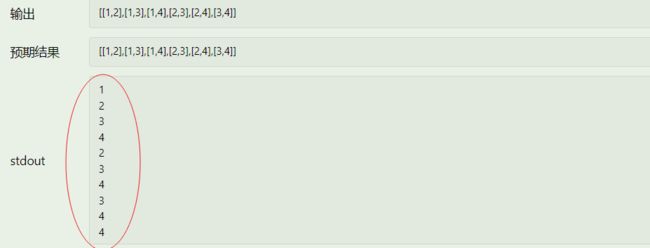 原始回溯
原始回溯
可以看到,for循环一共是10次:
- 1、2、3、4
- 2、3、4
- 3、4
- 4
等于说是从下标为1开始到4都进行了遍历;
剪枝方法1
参考【1】中给出的优化是这样子的:
class Solution:
def combine(self, n: int, k: int) -> List[List[int]]:
res=[] #存放符合条件结果的集合
path=[] #用来存放符合条件结果
def backtrack(n,k,startIndex):
if len(path) == k:
res.append(path[:])
return
for i in range(startIndex,n-(k-len(path))+2): #优化的地方
print(i) # 用于查看中间输出
path.append(i) #处理节点
backtrack(n,k,i+1) #递归
path.pop() #回溯,撤销处理的节点
backtrack(n,k,1)
return res
输出结果如下:
 剪枝方法1
剪枝方法1
可以看出上面一共输出了9次,等于循环中分别是
- 1、2、3、4
- 2、3、4
- 3、4
与最初的输出相比,等于说是优化了最后一个for。因为案例中k=2,所以倒数第二个数(3)之后的遍历都没有意义了。
剪枝方法2
仍然是参考【1】中的代码,只不过这次的代码变为如下:
class Solution(object):
def combine(self, n, k):
"""
:type n: int
:type k: int
:rtype: List[List[int]]
"""
result = []
path = []
def backtracking(n, k, startidx):
if len(path) == k:
result.append(path[:])
return
# 剪枝, 最后k - len(path)个节点直接构造结果,无需递归
last_startidx = n - (k - len(path)) + 1
result.append(path + [idx for idx in range(last_startidx, n + 1)])
for x in range(startidx, last_startidx):
print(x) # 输出中间变量
path.append(x)
backtracking(n, k, x + 1) # 递归
path.pop() # 回溯
backtracking(n, k, 1)
return result
看下中间输出:
 剪枝方法2
剪枝方法2
可以看到一共只有5次输出!
但是呢,仔细看下代码,这是因为在for循环上面有一个列表生成式:[idx for idx in range(last_startidx, n + 1)]
里面的for循环遍历了last_startidx到n + 1,而下面的for循环遍历了startidx到last_startidx,所以这两种方法实际上是一样的效果!!
提交记录对比:
方法1:
 方法1
方法1
方法2:
 方法2
方法2
看得出来方法2站时间上占优势,方法1在内存上占优势,但是两者相差比较小,但是个人认为方法2没有方法1直观形象。
剪枝剪了什么
看起来上面的剪枝方法与原来的方法比也就是少循环了一次,但是这种因为n=4,k=2,我们改成n=10,k=3再看下:
 不剪枝
不剪枝  剪枝方法1
剪枝方法1
对比可以发现,随着搜索空间的变大,剪枝方法的优化才能体现出来。
综上,剪枝就是在每一层的for循环中剪去一些不必要的遍历。
如何剪枝?
剪枝就是修剪for循环,那么怎么剪?
比如n=10,k=4,那么如果len(path)已经等于2了,那么在循环中从10开始遍历已经没有意义了,因为还有2个数字需要添加,但是从10开始只剩下一个了,所以要优化的是for循环的终止位置。
所以对应的终止位置就是n-(k-len(path))+2,这样子不好理解,拆开来看:
- 当前path中有len(path)个元素;
- 还需要再选出k-len(path)个元素, 但是会从startIndex到最终位置处再选出来一个;
- 所以说从当前for循环的终止位置后面的数据中还要选出k-len(path)-1个元素,如果剩下的待选小于这个数字了,自然就不用遍历了(也就是不用进入递归了)。 举个例子,如果从剩下的数据中还需要选3个,那么从倒数第二个自然就不用遍历了,因为没有意义了,也就是说for循环的终止位置坐标对应的就是n-(k-len(path)-1-1)(等于n-(k-len(path)+2)),所以才有了上面的代码(python中,一个list的倒数第k个元素,对应的下标是n-k)。
参考
【1】https://www.programmercarl.com/0077.%E7%BB%84%E5%90%88.html#%E5%85%B6%E4%BB%96%E8%AF%AD%E8%A8%80%E7%89%88%E6%9C%AC
本文由 mdnice 多平台发布