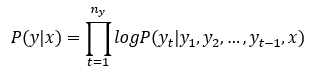【学习周报】研究生深度学习笔记9.19~9.24

学习目标：

• 深度学习花书
• SWINBERT: End-to-End Transformers with Sparse Attention for Video Captioning（CVPR 2022）

---

学习内容：

1. 花书配分函数——深度学习第十八章
2. 变分推断——深度学习第十九章
3. seq2seq概述
4. 深度学习端到端概念

---

学习时间：

• 9.19 ~ 9.24

---

学习笔记：

配分函数——深度学习第十八章

在深度学习第十六章——结构化概率模型的配分函数 (partition function) 中定义: 无向概率图模型可由非归一化的概率分布 $\tilde{p}(x;\theta )$ 来表示，为了使其归一化得到一个合理的概率分布，我们需要将其除以一个配分函数 $Z(\theta )$ ，得到归一化后的概率分布 $p(x;\theta )=\frac{1}{Z(\theta )}\tilde{p}(x;\theta )$ 。其中对于连续变量来说，$Z(\theta )=\int \tilde{p}(x;\theta )dx$ ，对于离散变量来说 $Z(\theta )={\sum }_x\tilde{p}(x;\theta )$ 。但对于许多模型来说，这个积分或者求和操作很难以处理，这一章就着重于如何有效的近似配分函数或如何绕过这一难题。

如果用最大似然法（最大似然法与最大后验概率估计——深度学习花书第五章）来处理概率图问题，则我们需要求模型概率分布相对于参数 $\theta$ 的对数似然梯度（log-likelihood）${▽}_{\theta }logp(x;\theta )={▽}_{\theta }log\tilde{p}(x;\theta )-{▽}_{\theta }logZ(\theta )$ 。如此，我们将其分解为两项，分别称为正相(positive phase) 与负相(negative phase)。通常，正相比较容易处理，而负相由于涉及到大量变量的求和或积分很难处理，但是利用 $Z(\theta )={\sum }_x\tilde{p}(x;\theta )$ 的定义，我们可以将负相转化为期望形式 ${▽}_{\theta }logZ(\theta )=E_{x\sim p(x)}{▽}_{\theta }log\tilde{p}(x)$ ，从而可以利用上一章中的蒙特卡洛方法（蒙特卡罗方法——深度学习第十七章）来近似这一项。

这种方法的基本思路是对于数据的每个minibatch，进行如下操作：

• 用输入的minibatch中的数据样本计算正相 ${▽}_{\theta }log\tilde{p}(x;\theta )$ 。
• 用Markov Chain生成一些模型样本，利用这些样本计算负相 $E_{x\sim p(x)}{▽}_{\theta }log\tilde{p}(x)$ 。
• 将正相负相结合，并利用梯度算法更新模型参数。

其中，正相和负相的关系如下图所示，正相是将模型的概率分布推向和真实数据分布一致的方向，负相是降低模型样本发生的分布，分别对应极大化 $log\tilde{p}$ 与极小化 $logZ$ 。

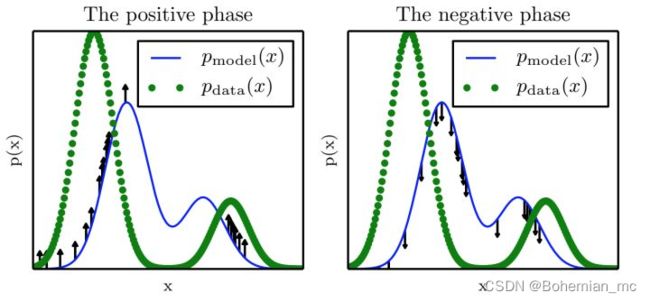
如果对于每个minibatch我们都重新随机初始化Markov Chain直至其达到平稳分布会需要花很长的时间，为了加快这一进程，我们可以采取如下方法：

对比散度(contrastive divergence) 方法不需要每个minibatch随机初始化Markov Chain，而是利用minibatch真实的数据样本来初始化Markov Chain，最初数据分布可能和模型分布有较大差异，因此负相计算有较大偏差，但正相可以逐渐的增加模型对应数据的概率分布，经过若干次后，模型分布逐渐趋于数据分布，负相也会更加准确。当然，如果模型分布过度偏离数据分布，则负相计算误差过大，这是该方法的一个缺点。

一个改进方法是持续对比发散(persistent contrastive divergence,简称PCD)，也叫做随机最大似然(stochastic maximum likelihood，简称SML)，其基本思想是对于每个minibatch，Markov Chain不用重新初始化，而是延续上一个minibatch时Markov Chain的状态，其基本假定是两次步进间模型差异较小，所以可以利用前次模型分布近似当前模型分布，这样就节省了每次重新初始化并达到稳态的混合时间。

蒙特卡洛方法近似了最大似然估计中配分函数的梯度，而还有一类方法试图绕过配分函数的复杂的求值问题，主要有如下几种方法：

• 伪似然(Pseudolikelihood) 利用条件概率分布来近似模型概率分布 $p(x;\theta )\approx {\prod }_{i}p(x_i|x_{-i};\theta )={\prod }_{i}p(x_i|x_{N(i)};\theta )$
  ，其中 $N(i)$ 代表了 在图中的所有邻居节点。其对数形式为 $logp(x;\theta )\approx {\sum }_{i}logp(x_i|x_{N(i)};\theta )$
  ，求和中的每一项只包含相应的一项变量，而不需要对全局的变量求配分函数。

• 得分匹配(score matching)目的是使模型与数据分布相对于输入数据的梯度差异 $L(x,\theta )=\frac{1}{2}||{▽}_{x}log{p}_{model}(x;\theta )-{▽}_{x}log{p}_{data}(x)|{|}_2^2$ 极小化，它利用了模型对输入数据 $x$ 的梯度而不是参数 $\theta$ 的梯度，由于 $Z$ 仅是关于 $\theta$ 的函数，${▽}_{x}Z=0$ ，所以绕过了对配分函数 $Z$ 的求值。

• 比率匹配(ratio matching) 主要适用于二元数据，其目的是极小化如下的目标函数 $L(x,\theta )={\sum }_{j=1}^n(\frac{1}{1+\frac{p_{model}(x;\theta )}{p_{model}(f(x,j);\theta )}}{)}^2$ ，其中 $f(x,j)$ 返回 $f(x,j)$ 在第j个位置上比特翻转的结果。由于是求两个概率的比值，配分函数可以互相抵消掉，因此绕过了对配分函数的求值。

另外，噪声对比估计(Noise Contrastive Estimation, 简称NCE) 提供了另外一种思路，即利用某个变量来近似配分函数 ${▽}_{\theta }log{p}_{model}(x)={▽}_{\theta }log{\tilde{p}}_{model}(x;\theta )+c$ ，其中 $c$ 是用来近似 $-logZ(\theta )$ 的参数，模型训练时同时学习参数 $\theta$ 和 $c$ 。当转化这种形式后，我们无法再用最大似然估计方法，因为它会选择将 $c$ 设置的无限大，而不是将其定为一个合理的概率分布。因此，NCE方法转而将无监督学习的估计 $p(x)$ 的问题转化为一个概率二分类器的监督学习问题，其中一类是模型产生的数据，另一类是一个新引入的噪声分布 $p_{noise}(x)$ ，该噪声分布易于评估与取样。现在，我们就可以构建一个新的分类模型，其输入为 $x$ ，二元分类标记为 $y$ 。

在此模型中：
$$\begin{gathered} p_{joint}(y=1)=\frac{1}{2} \\ {p}_{joint}(x|y=1)=p_{model}(x) \\ {p}_{joint}(x|y=0)=p_{noise}(x) \end{gathered}$$

因此可以将其转化为用 $p_{joint}$ 拟合 $p_{train}$ 的最大似然概率问题：
$\theta ,c=argma{x}_{\theta ,c}{E}_{x,y\sim p_{train}}log{p}_{joint}(y|x)$

由此可得到 $p_{joint}$ 实际上就是模型分布与噪声分布差异的逻辑回归模型：
$p_{joint}(y=1|x)=\sigma (log{p}_{model}(x)-log{p}_{noise}(x))$

可以看出，NCE的基本思想是好的模型可以分辨实际数据与噪声，在对抗生成网络中，好的生成模型可以产生使分类器无法分辨的样本，这一思想在对抗模型 GAN 中也会应用。

上述方法均是在模型训练时如何估计配分函数的梯度或者跳过配分函数的求值，当需要配分函数来求得最终归一化的概率分布的时候，如模型效果评测时，如何得到配分函数的值？

我们同样可以利用之前介绍的重要采样(importance sampling) 方法。

假设我们要求的配分函数为 $Z_1=\int {\tilde{p}}_1(x)dx$ ，这个配分函数难以处理，我们可以转化为较易处理的且配分函数易求得的分布 $p_0(x)=\frac{1}{Z_0}{\tilde{p}}_0(x)$ 根据重要采样方法有：
$Z_1=\int {\tilde{p}}_1(x)dx=\int \frac{p_0(x)}{p_0(x)}{\tilde{p}}_1(x)dx=Z_0\int p_0(x)\frac{{\tilde{p}}_1(x)}{{\tilde{p}}_0(x)}dx$

利用蒙特卡洛方法近似其期望有 ${\hat{Z}}_1=\frac{Z_0}{K}{\sum }_{k=1}^K\frac{{\tilde{p}}_1(x^{(k)})}{{\tilde{p}}_0(x^{(k)})}$。

当分布 $p_0$ 接近于 $p_1$ 时，上式可有效地估计配分函数，但实际情况中 $p_1$ 通常是高维空间的复杂分布，很难找到一个简单的分布 $p_0$ 既方便计算有能接近分布$p_1$，这个时候 $Z_1$ 的方差很大，无法有效的近似。在这一基础上，有两种改进方法可以解决当 $p_0$ 与 $p_1$ 的KL Divergence过大时出现的这一问题：

• 退火重要采样(Annealed Importance Sampling) 基本思想是用一系列接近的分布来连接 $p_0$ 与 $p_1$ 间的差距，即用一系列分布 $p_{{\eta }_0},...,p_{{\eta }_n}$ 其中 $0={\eta }_0<{\eta }_1<...<{\eta }_{n-1}<{\eta }_n=1$ ，其中第一个分布为 $p_0$，最后一个分布为 $p_1$。由此， $Z_1$ 与 $Z_0$ 的比值可以表示为 $\frac{Z_1}{Z_0}=\frac{Z_1}{Z_0}\frac{Z_{{\eta }_1}}{Z_{{\eta }_1}}...\frac{Z_{{\eta }_{n-1}}}{Z_{{\eta }_{n-1}}}=\frac{Z_{{\eta }_1}}{Z_0}\frac{Z_{{\eta }_2}}{Z_{{\eta }_1}}...\frac{Z_{{\eta }_{n-1}}}{Z_{{\eta }_{n-2}}}\frac{Z_1}{Z_{{\eta }_{n-1}}}={\prod }_{j=0}^{n-1}\frac{Z_{{\eta }_{j+1}}}{Z_{{\eta }_j}}$ 。如果我们保证每个 $p_{{\eta }_j}$ 与
  $p_{{\eta }_{j+1}}$ 都足够接近，则我们可以用重要采样来近似每个 $\frac{Z_{{\eta }_{j+1}}}{Z_{{\eta }_j}}$ ，最终可以得到 $\frac{Z_1}{Z_0}$ 。实际操作中，通常用加权几何平均来得到中间的概率分布 $p_{{\eta }_j}\propto p_1^{{\eta }_j}{p}_0^{1-{\eta }_j}$。

• 桥式采样(Bridge Sampling)，与退火重要采样相比，它不是利用一系列的分布，而仅仅利用一个中间分布 $p_{\ast }$ 来过渡 $p_0$ 与 $p_1$，即 $\frac{Z_1}{Z_0}={\sum }_{k=1}^K\frac{{\tilde{p}}_{\ast }(x_0^{(k)})}{{\tilde{p}}_0(x_0^{(k)})}/{\sum }_{k=1}^K\frac{{\tilde{p}}_{\ast }(x_1^{(k)})}{{\tilde{p}}_1(x_1^{(k)})}$ ，如果 $p_{\ast }$ 选取的合适使得其同 $p_0$ 与 $p_1$ 均有较大的重合，则可以在 $p_0$ 与 $p_1$ 分布间构建一个连通的桥梁， 最优的桥梁分布为 $p_{\ast }^{(opt)}(x)\propto \frac{{\tilde{p}}_0(x){\tilde{p}}_1(x)}{r{\tilde{p}}_0(x)+{\tilde{p}}_1(x)}$ ，其中 $r=\frac{Z_1}{Z_0}$ 。但是实际上我们并不知道比率 $r$ 且这正是我们要求的比值，实际操作中，通常我们猜测一个粗略的 $r$ 值，并不断的迭代改进桥梁分布即相应的比率的估值。

变分推断——深度学习第十九章

基本思路

在概率模型中，我们常常需要近似难以计算的概率分布，在贝叶斯统计中，所有的对于未知量的推断(inference) 问题可以看做是对后验概率(posterior) 的计算，而这一概率通常难以计算，利用MCMC马尔科夫链蒙特卡洛算法（参考蒙特卡罗方法——深度学习第十七章）可以做近似，但是对于大量数据，MCMC算法计算较慢，变分推断(Variational Inference) 就为我们提供了一种更快更简单的适用于大量数据的近似推断方法。

假定我们用 $x=x_{1:n}$ 代表我们输入的观察量，$z=z_{1:m}$ 代表模型中的隐藏变量，推断问题即为依据输入数据的后验条件概率分布 $p(z|x)$ 。变分法的基本思想是将这一问题转化为优化(optimization) 问题：

1. 首先，我们提出一族关于隐藏变量的近似概率分布 $Q$ ，我们希望从这一族分布中找到一个与真实的后验分布的KL Divergence，即 $q^{\ast }(z)=\underset{q(z)\in Q}{\mathrm{argmin}}KL(q(z)||p(z|x))$ 。
2. 之后，我们便可用 $q^{\ast }(z)$ 来近似代替真实的后验分布 $p(z|x)$ 。因此变分推断将推断问题转化为了求极值的优化问题，而的选择决定了优化问题的难易度，变分法核心思想就是要选定这一族函数使得密度分布足够灵活可以近似 $p(z|x)$ 的分布，同时又足够简单使得我们可以进行高效的优化。

与MCMC算法比较

MCMC方法是利用马尔科夫链取样来近似后验概率，变分法是利用优化结果来近似后验概率，两者的比较如下：

首先，MCMC相较于变分法计算上消耗更大，但是它可以保证取得与目标分布相同的样本，而变分法没有这个保证：它只能寻找到近似于目标分布一个密度分布，但同时变分法计算上更快，由于我们将其转化为了优化问题，所以可以利用诸如随机优化(stochastic optimization)或分布优化(distributed optimization)等方法快速的得到结果。所以当数据量较小时，我们可以用MCMC方法消耗更多的计算力但得到更精确的样本。当数据量较大时，我们用变分法处理比较合适。

另一方面，后验概率的分布形式也影响着我们的选择。比如对于有多个峰值的混合模型，MCMC可能只注重其中的一个峰而不能很好的描述其他峰值，而变分法对于此类问题即使样本量较小也可能优于MCMC方法。

变分推断详述

首先，可以将隐藏变量 $z$ 相对于观察量 $x$ 的条件概率写为 $p(z|x)=\frac{p(z,x)}{p(x)}$ ，其中分母是观察量的边缘分布，可以通过从联合分布中边缘化隐藏变量得到 $p(x)=\int p(z,x)dz$ ，这个函数又被称作evidence，通常这个积分需要指数级别的时间去计算，这也是为什么推断问题常常难于处理。

在变分推断中，不是直接求 $p(z|x)$ ，而是求与其KL divergence最小的优化问题

$q^{\ast }(z)=\underset{q(z)\in Q}{\mathrm{argmin}}KL(q(z)||p(z|x))$

其中 $KL(q(z)||p(z|x))=E[logq(z)]-E[logp(z|x)]$ ，期望$E$均是对于分布 $q(z)$ 上的期望。

可以将其进一步展开为 $KL(q(z)||p(z|x))=E[logq(z)]-E[logp(z,x)]+logp(x)$

最后一项为 $logp(x)$ ，我们又回到最初的边缘分布的问题难以求解。由于我们无法直接计算KL，所以我们改变优化目标为与KL前两项相关的量evidence lower bound（ELBO）： $ELBO(q)=E[logp(z,x)]-E[logq(z)]$

可以看到，ELBO是负的KL再加上 $logp(x)$ ，由于 $logp(x)$ 相对于 $q(z)$ 的梯度为零，所以极小化KL divergence的问题与极大化ELBO的优化问题是等价的。因此，我们将难以求解的KL极值问题转化为易于求解的对ELBO的极值问题。

观察ELBO的形式，也可以将其分解为：
$ELBO(q)=E[logp(z)]+E[logp(x|z)]-E[logq(z)]=E[logp(x|z)]-KL(q(z)||p(z))$
这一形式有助于我们理解ELBO的直观意义：第一项是个期望项，它促使模型将它的隐藏变量集中于可以解释观察量的配置上，第二项是隐藏变量变分分布与先验分布的KL divergence的相反数，它促使变分分布接近于先验分布，所以变分模型的目标函数是似然率与先验分布的一种平衡。

另外，可以将evidence $logp(x)$ 写成这样的形式：
$logp(x)=KL(q(z)||p(z|x))+ELBO(q)$

由于 $KL(q(z)||p(z|x))\ge 0$ ，所以 $ logp(\vec{x}) \geq ELBO(q)$ ，这也是ELBO(evidence lower bound)得名的原因，它提供了 $ logp(\vec{x})$ 的下限，当 $q(z)=p(z|x)$ 时，$ logp(\vec{x}) = ELBO(q)$ ，实际上EM算法（Expectation-Maximization) 就是利用了这一特征，它分为交替进行的两步：E step假设模型参数不变，$q(z)=p(z|x)$，计算对数似然率，在M step再做ELBO相对于模型参数的优化。与变分法比较，EM算法假设了当模型参数固定时，$p(z|x)$ 是易计算的形式，而变分法并无这一限制，对于条件概率难于计算的情况，变分法仍然有效。

在基本思路中，提到了近似概率分布$Q$，在实际问题中，$Q$该如何选择？

一个简单而有效的变分族为平均场变分族(mean-field variational family)。它假设了隐藏变量间是相互独立的：$q(z)={\prod }_{j=1}^m{q}_j(z_j)$ 。这个假设看起来似乎比较强，但实际应用范围还是比较广泛，可以将其延展为将有实际相互关联的隐藏变量分组，而化为各组联合分布的乘积形式即可。

利用ELBO和平均场假设，就可以利用coordinate ascent variational inference（简称CAVI)方法来处理：

利用条件概率分布的链式法则有 $p(z_{1:m},x_{1:n})=p(x_{1:n}){\prod }_{j=1}^{m}p(z_j|z_{1:(j-1)},x_{1:n})$

变分分布的期望为 $E[logq(z_{1:m})]={\sum }_{j=1}^m{E}_j[logq(z_j)]$ 。

将其代入ELBO的定义得到：
$ELBO=logp(x_{1:n})+{\sum }_{j=1}^{m}E[logp(z_j|z_{1:(j-1)},x_{1:n})]-E_j[logq(z_j)]$

将其对 $z_k$ 求导并令导数为零有 $\frac{dELBO}{dq(z_k)}=E_{-k}[logp(z_k|z_{-k},x)]-logq(z_k)-1=0$ ，由此得到coordinate ascent 的更新法则为 $q^{\ast }(z_k)\propto exp{E}_{-k}[logp(z_k,z_{-k},x)]$ 。我们可以利用这一法则不断的固定其他的 的坐标来更新当前的坐标对应的z值，这与Gibbs Sampling(参见蒙特卡罗方法——深度学习第十七章)过程类似，不过Gibbs Sampling是不断的从条件概率中采样，而CAVI算法中是不断的用如下形式更新：$q^{\ast }(z_k)\propto expE[log(conditional)]$ 。其完整算法如下所示：

混合高斯模型变分法实例

用变分法在混合高斯分布中的实例来直观的理解其训练过程，如下图所示，可以看出，随着训练的进行，可以逐渐的将各个不同的峰值分开，对应的ELBO也在不断的增大。

seq2seq概述

基本原理：

Encoder-decoder框架为文本处理领域的一种非常流行的框架，这项技术突破了传统的输入大小固定的问题，将深度神经网络模型用到了自然语言处理的相关任务之中。其不仅可以用在对话生成任务中，同样应用在自然语言处理的其他领域，如机器翻译、文本摘要、句法分析等任务中。

Seq2seq模型最早在2014年，由Ilya Sutskever等提出。当时主要应用在机器翻译的相关问题中，其可以理解为一个适用于处理由句子（段落）X生成句子（段落）Y的通用模型。对于给定的输入句子X，我们的目标是通过Seq2seq模型生成目标句子Y。X与Y并不限制为同一种语言。将X和Y的单词序列表示如下：

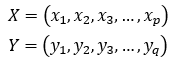
编码器(Encoder)对输入句子 进行建模，通过非线性变换将输入向量转化为中间向量表示h。

解码器(Decoder)根据编码器生成的中间向量表示 和之前的历史信息 ,生成i时刻的单词 。

其目标函数表示为：

上述目标函数存在数值下溢（Numerical Underflow） 的问题，原因每一项都小于1，乘起来就会得到很小的数字，因此在实际中往往取其对数进行放缩，训练目标即为最大化下面的目标函数。

经典改进：

Teacher foring

在基础的模型中，Decoder的每一次解码又会作为下一次解码的输入，这样就会导致一个问题就是错误累计，如果其中一个RNN单元解码出现误差了，那么这个误差就会传递到下一个RNN单元，使训练结果误差越来越大。Teacher Forcing[2]在一定程度上解决了这个问题，它的流程如图3所示，在训练过程中，使用要解码的序列作为输入进行训练，但是在inference阶段是不能使用的，因为你不知道要预测的序列是个啥，当然只在训练过程中效果就很不错了，它帮助模型加速收敛。

Attention

在传统的Seq2seq模型中，编码器将所有长度的原始句子都编码成一个固定维度的向量，若原始句子较长，这个向量往往不能很好地表达原始句子的所有细节，同时，这个向量的表达受最后位置的词的影响更大。Bahdanau[3]和Cho[4]利用注意力改进了Seq2seq模型。在加入了注意力机制的Seq2seq模型中，解码器在每一个位置的生成时，会利用编码器的所有状态加权作为输入，而非仅选取编码器的最后一个状态值。

Curriculum Learning

在模型的训练中的解码器部分，使用上一个时刻的输出作为下一个时刻的输入。这样会导致训练迭代过程早期的模型的预测能力非常弱，几乎不能给出好的生成结果。如果某一个时刻产生了垃圾结果，必然会影响后面整体的学习，以至于最终结果非常不好也很难溯源到发生错误的源头。我们在训练中使用课程学习（Curriculum Learning）[5]来改进这一问题，通过改变训练过程，以便逐步迫使模型处理它自己的错误，就像它在推断（Inference）过程中必须做的那样。具体地，以概率 去选择使用真实的输出 还是前一个时刻模型生成的输出 作为当前时刻的输入。概率 会随着时间的推移而减小，即使用计划抽样(Scheduled Sampling)的方法产生输入。这样在训练的早期阶段，模型可以获得更多真实的数据，从而加速训练；在训练的后期阶段，模型更多地使用真实输出作为输入，从而学习如何处理错误。

深度学习端到端概念

什么是端到端学习？

简而言之，以前有一些数据处理系统或者学习系统，它们需要多个阶段的处理。那么端到端深度学习就是忽略所有这些不同的阶段，用单个神经网络代替它。

以语音识别为例，目标是输入，比如说一段音频，然后把它映射到一个输出，就是这段音频的听写文本。传统上，语音识别需要很多阶段的处理。首先会提取一些特征，一些手工设计的音频特征，例如MFCC，这种算法是用来从音频中提取一组特定的人工设计的特征。在提取出一些低层次特征之后，可以应用机器学习算法在音频片段中找到音位，所以音位是声音的基本单位，比如说“Cat”这个词是三个音节构成的，Cu-、Ah-和 Tu-，算法就把这三个音位提取出来，然后将音位串在一起构成独立的词，再将词串起来构成音频片段的听写文本。

端到端深度学习做的是训练一个巨大的神经网络，输入就是一段音频，输出直接是听写文本。端到端深度学习只需要把训练集拿过来，直接学到了和之间的函数映射，直接绕过了其中很多步骤。

是否要使用端到端的深度学习？

端到端学习的优点：

• 首先，端到端学习真正做到了让数据说话。如果有足够多的(,)数据，那么不管从到最适合的函数映射是什么，只需要训练一个足够大的神经网络来让这个神经网络自己搞清楚。
• 其次，所需手工设计的组件更少，这能够简化设计工作流程，不需要花太多时间去手工设计功能以及中间表示方式。

端到端学习的缺点：

• 首先，它可能需要大量的数据。要直接学到这个到的映射，可能需要大量(, )数据。例如在人脸识别任务中，可以收集很多数据用来分辨图像中的人脸，当找到一张人脸后，也可以找得到很多人脸识别数据。但是对于整个端到端任务，能用的数据可能很少。
• 其次，它排除了可能有用的手工设计组件。机器学习研究人员一般都很鄙视手工设计的东西，但如果没有很多数据，学习算法就没办法从很小的训练集数据中获得洞察力。在这种情况下，手工设计组件就显得很有价值，即将人类对这个问题的很多认识直接注入到算法里，这对于解决问题来说很有必要。