PDE优化|逆问题中偏微分方程约束优化的惩罚方法（Matlab代码实现）

 欢迎来到本博客❤️❤️❤️

本文目录如下：⛳️⛳️⛳️

​ 

目录

1 概述

2 数学模型

3 算例及仿真结果

 4 结论

5 Matlab代码实现

---

1 概述

在逆问题中，目标是从间接观察中推断物理参数（例如密度、声速或电导率）。当基础模型由偏微分方程 (PDE)（例如，波动方程或麦克斯韦方程）描述时，观察到的数据通常是多个右手边 PDE 解的部分测量值。这些参数通常显示为 PDE 中的系数。这些问题出现在许多应用中，例如地球物理学 [1、2、3、4]、医学成像 [5、6] 和无损检测。

许多逆和参数估计问题可以写成偏微分方程约束的优化问题。因此，目标是从几个右侧偏微分方程解的部分测量中推断出参数，通常是偏微分方程的系数。这种偏微分方程约束的问题可以通过找到拉格朗日量的静止点来解决，这需要同时更新参数和（伴随）状态变量。对于大规模问题，这种一次性全部的方法不可行，因为它需要存储所有状态变量。在这种情况下，人们通常采用简化方法，其中通过求解偏微分方程来显式消除约束（在每次迭代中）。这两种方法及其变体是解决由逆问题引起的偏微分方程约束优化问题的主要主力。在本文中，我们提出了一种替代方法，旨在结合这两种方法的优点。我们的方法基于约束优化问题的二次惩罚公式。通过消除状态变量，我们开发了一种有效的算法，该算法具有与传统简化方法大致相同的计算复杂性，同时利用更大的搜索空间。数值结果表明，该方法确实降低了问题的一些非线性，并且对初始迭代的敏感性较低。

2 数学模型

对于线性偏微分方程，可以将逆问题（离散化后）表述为以下形式的约束优化问题：

                      

在实践中，通常在公式 (1) 中包含一个正则化项，以减轻问题的不适定性。然而，为了简化讨论，忽略了这些术语，因为可以在需要时添加适当的正则化术语。

在由逆问题引起的应用中，约束问题 (1) 通常使用拉格朗日乘数 [7, 8] 或顺序二次规划 (SQP) [9, 10] 的方法来解决。这需要同时优化参数、状态和拉格朗日乘数（或伴随状态变量）。虽然从优化的角度来看，这种一次性方法通常非常有吸引力，但它们通常不适用于大规模问题，因为我们无法同时存储所有 K 个实验的状态变量。相反，所谓的简化方法是基于（块）消除约束来制定参数上的无约束优化问题：

                        

如果对状态进行完整测量（即 P 是可逆的），则所述逆问题将更容易解决。在这种情况下，我们可以从数据中重建状态为 u = P−1d，然后通过求解来恢复参数：

                      

详细数学模型见第4部分。

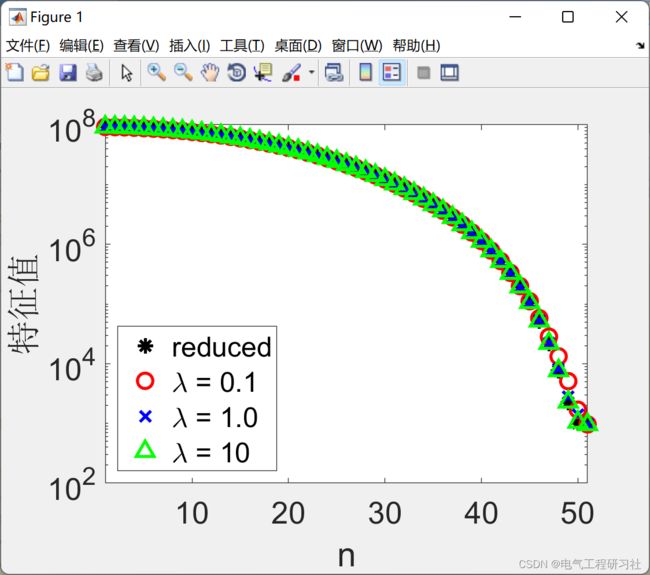
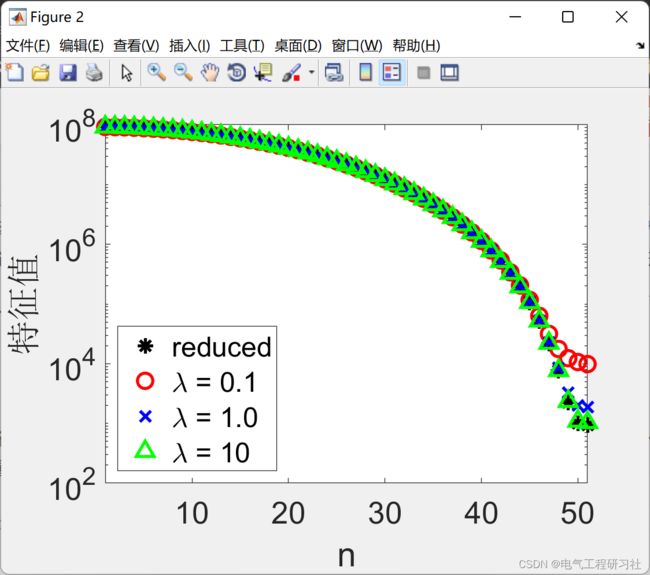
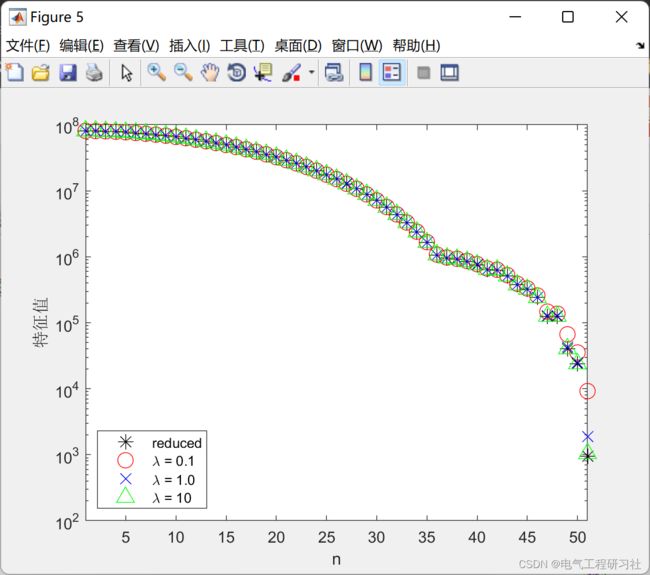
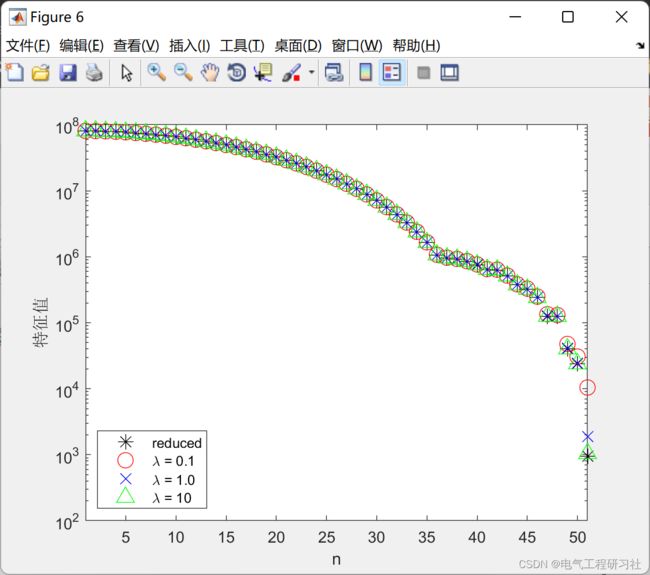
3 算例及仿真结果

 

 

 

 

部分代码：

n  = 51;
f  = 5;
x  = linspace(0,1,n-1);
h  = x(2) - x(1);
mt = ones(n-1,1);
omega = 2*pi*f;

D  = spdiags(ones(n,1)*[-1 1]/h,[0:1],n-1,n);
w  = ones(n,1); w([1 end]) = .5;
At = (1i*omega)*diags(w) + D'*diags(mt)*D;

[Vr,Dr] = eig(full(At'*At)); [Dr,Ir] = sort(diag(Dr),'descend'); Vr = Vr(:,Ir);
kappar  = Dr(1)/Dr(end);

a  = [1e-1 1 1e1];
L  = [1 10 20];
ls = {'ro','bx','g^'};

P{1} = speye(n);
P{2} = fft(eye(n))/sqrt(n);

for k = 1:1
    for l = 1:length(L)  
        %I = randperm(n); I  = I(1:L(l));
        I = round(linspace(1,n,L(l)));
        Pl = P{k}(:,I);

        mu = eigmax(@(x)At'\(Pl*Pl'*(At\x)),n);

        figure;semilogy(1:n,Dr,'k*','markersize',10);hold on;
        xlabel('n');ylabel('特征值');xlim([1 n]);

        for i = 1:length(a)
            lambda = a(i)*real(mu);
            B = (At'*At) + (1/lambda)*(Pl*Pl');
            %[Vp,Dp] = eig(full(diags(1./Dr)*ex(Vr'*B*Vr))); [Dp,Ip] = sort(diag(Dp),'descend'); Vp = Vp(:,Ip);
            [Vp,Dp] = eig(full(B)); [Dp,Ip] = sort(diag(Dp),'descend'); Vp = Vp(:,Ip);
            kappap(l,i) = Dp(1)/Dp(end);
            lower = 1/(1+L(l)/(lambda*Dr(end)));
            upper =   (1+L(l)/(lambda*Dr(1)));
            
            semilogy(1:n,abs(Dp),ls{i},'markersize',10);hold on;
        end
        legend('reduced',['\lambda = 0.1'],['\lambda = 1.0'],['\lambda = 10'],'location','SouthWest');
    end

    kappa{k} = kappap/kappar;
end

savefig(1:3,'../../doc/figs/example2');

latextable(kappa{1},'Horiz',{'$\lambda = 0.1$','$\lambda = 1$','$\lambda = 10$'},'Vert',{['L = ' num2str(L(1))],['L = ' num2str(L(2))],['L = ' num2str(L(3))] },'Hline',[1 NaN],'format','%1.2e','name','../../doc/figs/example2.tex');

 4 结论

本文提出了一种使用线性 PDE 进行 PDE 约束优化的惩罚方法，并应用于逆问题。该方法基于约束问题的二次惩罚公式。这种重新表述导致参数和状态变量中的无约束优化问题。为了避免在优化过程中必须存储和更新状态变量，我们通过求解超定线性系统来显式消除状态变量。所提出的方法结合了同时更新状态和参数的 all-at-once 方法和显式消除 PDE 约束的传统简化方法的特征。虽然具有与传统简化方法相似的计算复杂度，但惩罚方法通过不完全满足 PDE 约束来探索更大的搜索空间。我们表明，只要惩罚参数 λ 选择得足够大，我们就可以（理论上）在给定的容差内找到约束问题的拉格朗日的驻点。虽然理论上我们需要 λ ↑∞，但我们可以解决有限 λ 在有限精度内到达静止点的问题。与传统简化方法的主要算法差异是从问题中消除状态的方式。我们没有求解 PDE，而是制定了一个由离散 PDE 和测量值组成的超定方程组。我们讨论了这个增强系统的性质，并用几个数值例子表明，与原始 PDE 相比，系统的结构和特征值都没有发生显着变化。因此，使用与原始 PDE 相同的方法可以有效地求解增强系统是合理的。数值示例表明，即使使用单个相对较小的 λ 值，也可以获得非常好的结果。 ad-hoc 延续策略进一步表明，逐渐增加 λ 以达到所需的容差是可行的。

5 Matlab代码实现

博客主页：电气辅导帮