时间序列分析 Python与statsmodels实现ARMA模型
宝藏网站(官方文档):Time Series Analysis
建模步骤
1.平稳性和纯随机性检验
平稳性和纯随机性检验的重要性:
ARMA、ARIMA模型都建立在时间序列为平稳非白噪声序列的假设下。
平稳性检验
方法:时序图检验,自相关图检验,单位根检验
简单介绍**单位根检验(ADF检验)**代码如下(使用statsmodels下的adfuller):
def adf_test(timeseries): # 传入时间序列
print ('Results of Dickey-Fuller Test:')
dftest = adfuller(timeseries, autolag='AIC')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)'%key] = value
print (dfoutput)
此函数给出了p值以及显著性水平,p值小于显著性水平—检验通过;如果检验不通过----差分
纯随机性检验(白噪声检验):
方法:Q检验(Box-Pierce检验),Ljung-Box 检验
下面介绍LB检验和Q检验(使用statsmodels下的acorr_ljungbox)(这个函数虽然名字叫做lb检验,但是同时可以做Q检验):
# 此处以ARMA模型的残差为例
import statsmodels.api as sm
data = sm.datasets.sunspots.load_pandas().data
res = sm.tsa.ARMA(data["SUNACTIVITY"], (1,1)).fit(disp=-1)
sm.stats.acorr_ljungbox(res.resid, lags=[i for i in range(0,10)], return_df=True)
Out[]:
lb_stat lb_pvalue bp_stat bp_pvalue
1 9.649067 1.894478e-03 9.555989 1.992981e-03
2 28.423478 6.728528e-07 28.088929 7.953652e-07
3 45.542304 7.095811e-10 44.932532 9.563278e-10
4 62.784625 7.532410e-13 61.842204 1.189088e-12
5 107.864891 1.157704e-21 105.907801 2.998243e-21
6 135.381429 9.443966e-27 132.716518 3.442085e-26
7 143.063541 1.158902e-27 140.176319 4.668506e-27
8 143.123924 5.312026e-27 140.234761 2.120531e-26
9 168.862386 1.064818e-31 165.062858 6.579027e-31
10 214.106911 1.827445e-40 208.561614 2.635388e-39
我们取显著性水平为0.05,可以看出,所有滞后阶数(lags)的LB检验的p-value(第2列)都小于0.05;则我们拒绝原假设H0,即我们认为该序列是序列相关的(非白噪声序列、检验通过)。
同样取显著性水平为0.05,所有的BP检验的p-value(第4列)都小于0.05;则我们拒绝原假设 H 0 H_0 H0,即我们认为该序列是序列相关的(非白噪声序列、检验通过)。
2.建立ARIMA模型
假如某个观察值序列通过序列预处理,可以判定为平稳非白噪声序列,我们就可以利用模型对该序列建模。
建模步骤
(1) 求出该观察值序列的样本自相关系数(ACF)和样本偏自相关系数(PACF)的值。
(2) 根据样本自相关系数和偏自相关系数的性质,选择阶数适当的ARMA(p,q)模型进行拟合。(或ARIMA(p,d,q),d表示差分阶数)
(3) 估计模型中未知参数的值。
(4) 检验模型的有效性。如果拟合模型通不过检验,转向步骤(2),重新选择模型再拟合。
(5) 模型优化。如果拟合模型通过检验,仍然转向步骤(2),充分考虑各种可能,建立多个拟合模型,从所有通过检验的拟合模型中选择最优模型。
(6) 利用拟合模型,预测序列的将来走势。
ARMA模型阶数确定原则
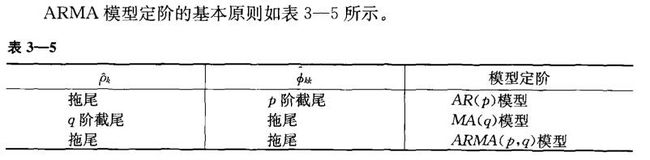
但是在实践中,这个定阶原则在操作上具有一定的困难。由于样本的随机性,样本的相关系数不会呈现出理论截尾的完美情况,本应截尾的样本自相关系数或偏自相关系数仍会呈现出小值振荡的情况。同时,由于平稳时间序列通常都具有短期相关性,随着延迟阶数 k → ∞ k\rightarrow \infty k→∞, ρ ^ 0 \hat\rho_{0} ρ^0与 ϕ ^ k k \hat\phi_{kk} ϕ^kk都会衰减至零值附近作小值波动。
解决方案:
1.凭经验(emm所以说这个检验的意义何在)。。
2.有人证明可以结合自相关系数和偏自相关系数的分布来判断。
Python下ARMA模型的statsmodels实现方法(包括绘制自相关图acf、偏自相关图pacf)
查看示例代码:Autoregressive Moving Average (ARMA): Sunspots data
创建一个ARMA模型报告
import statsmodels.api as sm
data = sm.datasets.sunspots.load_pandas().data
print(sm.tsa.ARMA(data["SUNACTIVITY"],(1,1)).fit(disp=-1).summary())
Out[]:
ARMA Model Results
==============================================================================
Dep. Variable: SUNACTIVITY No. Observations: 309
Model: ARMA(1, 1) Log Likelihood -1352.613
Method: css-mle S.D. of innovations 19.214
Date: Mon, 25 Jan 2021 AIC 2713.226
Time: 22:44:57 BIC 2728.160
Sample: 0 HQIC 2719.197
=====================================================================================
coef std err z P>|z| [0.025 0.975]
-------------------------------------------------------------------------------------
const 48.7970 6.219 7.847 0.000 36.609 60.985
ar.L1.SUNACTIVITY 0.7355 0.041 18.035 0.000 0.656 0.815
ma.L1.SUNACTIVITY 0.5194 0.041 12.810 0.000 0.440 0.599
Roots
=============================================================================
Real Imaginary Modulus Frequency
-----------------------------------------------------------------------------
AR.1 1.3596 +0.0000j 1.3596 0.0000
MA.1 -1.9252 +0.0000j 1.9252 0.5000
-----------------------------------------------------------------------------
一个简单的方法判断我们的模型是正确的:单位根完全落在单位圆之外----Roots下面的单位根AR.1和MA.1(其中Real 和 Imaginary表示实部和虚部),它们的模(Modulus)>1。ok检验通过。
同样也可以做ARIMA的。
绘制预测曲线
fig = sm.tsa.ARMA(data["SUNACTIVITY"], (1,1)).fit(disp=-1).plot_predict()
fig.savefig(dpi=1000)
# 此函数返回的是matplotlib的fig对象。
计算均方误差
err = data["SUNACTIVITY"] - sm.tsa.ARMA(data["SUNACTIVITY"], (1,1)).fit(disp=-1).predict()
print((err*err).sum()/err.shape)
[373.98640872]
记得有个老师说过,其实真正的统计建模。它的统计指标诊断只是指导性的。有时候很难完全通过检验。它并不能完全主导我们建模的整个过程。
另外,因为这个库没有中文翻译,强烈建议查看statsmodels的众多官方示例:Time Series Analysis