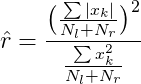图像质量评估
拍照容易,但拍出高质量的照片却很难。它需要良好的构图和照明。合适的镜头和卓越的设备可以产生很大的不同。但最重要的是,高质量的照片需要良好的品味和判断力。你需要专家的眼光。
但是,是否有一种数学质量度量可以捕捉这种人类判断?
答案是肯定的和否定的!
有一些质量度量很容易被算法捕获。例如,我们可以查看像素捕获的信息并将图像标记为嘈杂或模糊。
另一方面,算法几乎不可能捕获某些质量度量。例如,算法很难评估需要文化背景的图片的质量。
1.什么是图像质量评估(IQA)?
图像质量评估(IQA)算法以任意图像作为输入,输出质量分数作为输出。IQA有三种类型:
Full-Reference IQA:在这里,您有一个“干净”的参考(未失真)图像来测量失真图像的质量。该度量可用于评估图像压缩算法的质量,其中我们可以访问原始图像及其压缩版本图像。Reduced-Reference IQA:在这里,您没有参考图像,而是具有一些关于它的选择性信息的图像(例如水印图像),以比较和测量失真图像的质量。Objective Blind or No-Reference IQA:算法获得的唯一输入是您要测量其质量的图像。
2.传统图像质量评价指标:PSNR,SSIM,IEF,UQI
记噪声图为 X X X,滤波后的图像为 F F F,标准图像为 O O O。 M , N M,N M,N为图像的两个维度的大小。
2.1 Peak Signal to Noise Ratio (PSNR)峰值信噪比
如果图像是8位灰度图像,则: P S N R = 10 l o g ( 25 5 2 M S E ) PSNR = 10log(\frac{255^2}{MSE}) PSNR=10log(MSE2552)
其中: M S E MSE MSE为均方差误差:
M S E = 1 M ∗ N ∑ i = 0 M − 1 ∑ j = 0 N − 1 [ O ( i , j ) − F ( i , j ) ] 2 MSE=\frac{1}{M*N}\sum^{M-1}_{i=0}\sum^{N-1}_{j=0}{[O(i,j)-F(i,j)]^2} MSE=M∗N1i=0∑M−1j=0∑N−1[O(i,j)−F(i,j)]2
PSNR值越大,图像质量越高。
2.2 Structural Similarity Index Metric(SSIM)结构相似性
S S I M ( O , F ) = ( 2 μ O μ F + c 1 ) ( 2 σ O F + c 2 ) ( μ O 2 + μ F 2 + c 1 ) ( μ O 2 + μ F 2 + c 2 ) SSIM(O,F)=\frac{(2\mu_O\mu_F+c_1)(2\sigma_{OF}+c2)}{(\mu^2_O+\mu^2_F+c_1)(\mu^2_O+\mu^2_F+c_2)} SSIM(O,F)=(μO2+μF2+c1)(μO2+μF2+c2)(2μOμF+c1)(2σOF+c2)
其中, μ O , μ F , σ O 2 , σ F 2 和 σ O F 分 别 是 图 像 O 和 F 的 平 均 强 度 、 标 准 差 和 协 方 差 。 \mu_O,\mu_F,\sigma^2_O,\sigma^2_F和\sigma_{OF}分别是图像O和F的平均强度、标准差和协方差。 μO,μF,σO2,σF2和σOF分别是图像O和F的平均强度、标准差和协方差。
μ O = 1 M ∗ N ∑ i = 0 M − 1 ∑ j = 0 N − 1 O ( i , j ) μ F = 1 M ∗ N ∑ i = 0 M − 1 ∑ j = 0 N − 1 F ( i , j ) σ F = ( 1 M ∗ N − 1 ∑ i = 0 M − 1 ∑ j = 0 N − 1 [ F ( i , j ) − μ F ] 2 ) 1 2 σ O = ( 1 M ∗ N − 1 ∑ i = 0 M − 1 ∑ j = 0 N − 1 [ O ( i , j ) − μ O ] 2 ) 1 2 σ O F = ( 1 M ∗ N − 1 ∑ i = 0 M − 1 ∑ j = 0 N − 1 [ O ( i , j ) − μ O ] [ F ( i , j ) − μ F ] ) 1 2 \mu_O=\frac{1}{M*N}\sum^{M-1}_{i=0}\sum^{N-1}_{j=0}{O(i,j)}\\ \mu_F=\frac{1}{M*N}\sum^{M-1}_{i=0}\sum^{N-1}_{j=0}{F(i,j)}\\ \sigma_F=(\frac{1}{M*N-1}\sum^{M-1}_{i=0}\sum^{N-1}_{j=0}{[F(i,j)-\mu_F]^2})^{\frac{1}{2}}\\ \sigma_O=(\frac{1}{M*N-1}\sum^{M-1}_{i=0}\sum^{N-1}_{j=0}{[O(i,j)-\mu_O]^2})^{\frac{1}{2}}\\ \sigma_{OF}=(\frac{1}{M*N-1}\sum^{M-1}_{i=0}\sum^{N-1}_{j=0}{[O(i,j)-\mu_O][F(i,j)-\mu_F]})^{\frac{1}{2}} μO=M∗N1i=0∑M−1j=0∑N−1O(i,j)μF=M∗N1i=0∑M−1j=0∑N−1F(i,j)σF=(M∗N−11i=0∑M−1j=0∑N−1[F(i,j)−μF]2)21σO=(M∗N−11i=0∑M−1j=0∑N−1[O(i,j)−μO]2)21σOF=(M∗N−11i=0∑M−1j=0∑N−1[O(i,j)−μO][F(i,j)−μF])21
c 1 = ( K 1 L ) 2 , c 2 = ( K 2 L ) 2 c_1=(K_1L)^2, c_2=(K_2L)^2 c1=(K1L)2,c2=(K2L)2,对于8位灰度的图像 L = 255 L=255 L=255,常数 k 1 = 0.01 , k 2 = 0.03 k_1=0.01,k2=0.03 k1=0.01,k2=0.03
SSIM值越大,图像质量越好
2.3 Image Enhancement Factor (IEF)图像增强因子
I E F = ∑ i = 0 M − 1 ∑ j = 0 N − 1 [ X ( i , j ) − μ O ] 2 ∑ i = 0 M − 1 ∑ j = 0 N − 1 [ F ( i , j ) − μ O ] 2 IEF=\frac{\sum^{M-1}_{i=0}\sum^{N-1}_{j=0}{[X(i,j)-\mu_O]^2}}{\sum^{M-1}_{i=0}\sum^{N-1}_{j=0}{[F(i,j)-\mu_O]^2}} IEF=∑i=0M−1∑j=0N−1[F(i,j)−μO]2∑i=0M−1∑j=0N−1[X(i,j)−μO]2
IEF值越大,图像质量越好
2.4 Universal Quality Index (UQI)通用质量指标
U Q I = 4 μ O μ F σ O F ( μ O 2 + μ F 2 ) ( σ O 2 + σ F 2 ) UQI=\frac{4\mu_O\mu_F\sigma_{OF}}{(\mu^2_O+\mu^2_F)(\sigma^2_O+\sigma^2_F)} UQI=(μO2+μF2)(σO2+σF2)4μOμFσOF
UQI值越大,图像质量越好
2.5代码实现
import numpy as np
class ImageEvalue(object):
def image_mean(self, image):
mean = np.mean(image)
return mean
def image_var(self, image, mean):
m, n = np.shape(image)
var = np.sqrt(np.sum((image - mean) ** 2) / (m * n - 1))
return var
def images_cov(self, image1, image2, mean1, mean2):
m, n = np.shape(image1)
cov = np.sum((image1 - mean1) * (image2 - mean2)) / (m * n - 1)
return cov
def PSNR(self, O, F):
'''
:param O: 原始图像
:param F: 滤波后的图像
'''
MES = np.mean((np.array(O) - np.array(F)) ** 2)
PSNR = 10 * np.log10(255 ** 2 / MES)
return PSNR
def SSIM(self, O, F):
'''
:param O: 原始图像
:param F: 滤波后的图像
'''
c1 = (0.01 * 255) ** 2
c2 = (0.03 * 255) ** 2
meanO = self.image_mean(O)
meanF = self.image_mean(F)
varO = self.image_var(O, meanO)
varF = self.image_var(O, meanF)
covOF = self.images_cov(O, F, meanO, meanF)
SSIM = (2 * meanO * meanF + c1) * (2 * covOF + c2) / (
(meanO ** 2 + meanF ** 2 + c1) * (varO ** 2 + varF ** 2 + c2))
return SSIM
def IEF(self, O, F, X):
'''
:param O: 原始图像
:param F: 滤波后的图像
:param X: 噪声图像
'''
IEF = np.sum((X - O) ** 2) / np.sum((F - O) ** 2)
return IEF
def UQI(self, O, F):
'''
:param O: 原始图像
:param F: 滤波后的图像
'''
meanO = self.image_mean(O)
meanF = self.image_mean(F)
varO = self.image_var(O, meanO)
varF = self.image_var(F, meanF)
covOF = self.images_cov(O, F, meanO, meanF)
UQI = 4 * meanO * meanF * covOF / ((meanO ** 2 + meanF ** 2) * (varO ** 2 + varF ** 2))
return UQI
if __name__ == '__main__':
import cv2
objectPath = "monalisa.jpg"
filteredPath = "monalisa_noisy.jpg"
obj = cv2.imread(objectPath)
fil = cv2.imread(filteredPath)
imageEva = ImageEvalue()
print("PSNR: ", imageEva.PSNR(obj, fil))
print("SSIM: ", imageEva.SSIM(obj, fil))
print("IEF: ", imageEva.IEF(obj, fil, fil))
print("UQI: ", imageEva.UQI(obj, fil))
# PSNR: 28.85540647761987
# SSIM: 0.9514112121745085
# IEF: 1.0
# UQI: 0.929498884845049
2.6代码实现所用图像
3.Deep CNN-Based Blind Image Quality Predictor (DIQA)基于深度 CNN 的图像质量评估
3.1什么是DIQA?
DIQA将深度学习应用于图像质量评估(IQA)的一些最令人担忧的挑战。相对于其他方法的优势是:
- 该模型并不仅限于使用自然场景统计(NSS)图像
- 通过将训练分为两个阶段(1)特征学习和(2)将学习到的特征映射到主观分数来防止过拟合。
3.2 问题
为IQA生成数据集的成本很高,因为它需要专家监督。因此,基本的IQA基准仅仅由几千条数据组成。后者使深度学习模型的创建变得复杂,因为它们需要大量的训练样本来进行泛化。
例如,让我们考虑最常用的用于训练和评估IQA方法的数据集Live, TID2008, TID2013, CSIQ。下表中包含了每个数据集的总体总结:

样本总数不超过 4,000 条记录。
3.3 代码实现
具体实现连接如下:https://towardsdatascience.com/deep-image-quality-assessment-with-tensorflow-2-0-69ed8c32f195
# 分数越低图像质量越好,反之亦然
# pip install image-quality
import imquality.brisque as brisque
import PIL.Image
import matplotlib.pyplot as plt
path1 = '1.jpg'
path2 = '2.jpg'
# 读取图片
img1 = PIL.Image.open(path1)
plt.imshow(img1)
plt.axis('off')
# 对以上图像质量评估
print("image-quality {}".format(brisque.score(img1)))
# 读取图片
img2 = PIL.Image.open(path2)
plt.imshow(img2)
plt.axis('off')
# 对以上图像质量评估
print("image-quality {}".format(brisque.score(img2)))
3.4 图像
4.Blind/referenceless image spatial quality evaluator (BRISQUE)
在本节中,我们将基于python逐步实现 BRISQUE 方法。
BRISQUE是一种仅使用图像像素来计算特征的模型(其他方法是基于图像到其他空间的变换,如小波或 DCT)。它被证明是高效的,因为它不需要任何转换来计算其特征。 BRISQUE 依赖于空间域中局部归一化亮度系数的空间自然场景统计 (NSS) 模型,以及这些系数的两两乘积之和模型。
链接:https://pan.baidu.com/s/1gB2buLZKioYoPw3LXLAuHg
提取码:123a
4.1 代码展示
#!/usr/bin/python3
# -*- encoding: utf-8 -*-
import collections
from itertools import chain
import urllib.request as request
import pickle
import numpy as np
import scipy.signal as signal
import scipy.special as special
import scipy.optimize as optimize
import matplotlib.pyplot as plt
import skimage.io
import skimage.transform
import cv2
from libsvm import svmutil
# 空间域的自然场景统计(NSS)
# # 作者得到局部均值的方式可能有点令人困惑,它只是对图像应用了高斯滤波器。
def normalize_kernel(kernel):
return kernel / np.sum(kernel)
def gaussian_kernel2d(n, sigma):
Y, X = np.indices((n, n)) - int(n / 2)
gaussian_kernel = 1 / (2 * np.pi * sigma ** 2) * np.exp(-(X ** 2 + Y ** 2) / (2 * sigma ** 2))
return normalize_kernel(gaussian_kernel)
def local_mean(image, kernel):
return signal.convolve2d(image, kernel, 'same')
# 然后计算局部偏差
def local_deviation(image, local_mean, kernel):
"Vectorized approximation of local deviation"
sigma = image ** 2
sigma = signal.convolve2d(sigma, kernel, 'same')
return np.sqrt(np.abs(local_mean ** 2 - sigma))
# 最后,我们计算了MSCN系数
def calculate_mscn_coefficients(image, kernel_size=6, sigma=7 / 6):
C = 1 / 255
kernel = gaussian_kernel2d(kernel_size, sigma=sigma)
local_mean = signal.convolve2d(image, kernel, 'same')
local_var = local_deviation(image, local_mean, kernel)
return (image - local_mean) / (local_var + C)
# 作者发现,在更广泛的失真图像中,MSCN系数呈广义高斯分布。
def generalized_gaussian_dist(x, alpha, sigma):
beta = sigma * np.sqrt(special.gamma(1 / alpha) / special.gamma(3 / alpha))
coefficient = alpha / (2 * beta() * special.gamma(1 / alpha))
return coefficient * np.exp(-(np.abs(x) / beta) ** alpha)
# 相邻 MSCN 系数两两相乘
def calculate_pair_product_coefficients(mscn_coefficients):
return collections.OrderedDict({
'mscn': mscn_coefficients,
'horizontal': mscn_coefficients[:, :-1] * mscn_coefficients[:, 1:],
'vertical': mscn_coefficients[:-1, :] * mscn_coefficients[1:, :],
'main_diagonal': mscn_coefficients[:-1, :-1] * mscn_coefficients[1:, 1:],
'secondary_diagonal': mscn_coefficients[1:, :-1] * mscn_coefficients[:-1, 1:]
})
# 作者提到广义高斯分布不能很好地拟合系数乘积的经验直方图。因此,他们提出了非对称广义高斯分布 (AGGD) 模型
def asymmetric_generalized_gaussian(x, nu, sigma_l, sigma_r):
def beta(sigma):
return sigma * np.sqrt(special.gamma(1 / nu) / special.gamma(3 / nu))
coefficient = nu / ((beta(sigma_l) + beta(sigma_r)) * special.gamma(1 / nu))
f = lambda x, sigma: coefficient * np.exp(-(x / beta(sigma)) ** nu)
return np.where(x < 0, f(-x, sigma_l), f(x, sigma_r))
# 非对称广义高斯分布的拟合方法
def asymmetric_generalized_gaussian_fit(x):
def estimate_phi(alpha):
numerator = special.gamma(2 / alpha) ** 2
denominator = special.gamma(1 / alpha) * special.gamma(3 / alpha)
return numerator / denominator
def estimate_r_hat(x):
size = np.prod(x.shape)
return (np.sum(np.abs(x)) / size) ** 2 / (np.sum(x ** 2) / size)
def estimate_R_hat(r_hat, gamma):
numerator = (gamma ** 3 + 1) * (gamma + 1)
denominator = (gamma ** 2 + 1) ** 2
return r_hat * numerator / denominator
def mean_squares_sum(x, filter=lambda z: z == z):
filtered_values = x[filter(x)]
squares_sum = np.sum(filtered_values ** 2)
return squares_sum / ((filtered_values.shape))
def estimate_gamma(x):
left_squares = mean_squares_sum(x, lambda z: z < 0)
right_squares = mean_squares_sum(x, lambda z: z >= 0)
return np.sqrt(left_squares) / np.sqrt(right_squares)
def estimate_alpha(x):
r_hat = estimate_r_hat(x)
gamma = estimate_gamma(x)
R_hat = estimate_R_hat(r_hat, gamma)
solution = optimize.root(lambda z: estimate_phi(z) - R_hat, [0.2]).x
return solution[0]
def estimate_sigma(x, alpha, filter=lambda z: z < 0):
return np.sqrt(mean_squares_sum(x, filter))
def estimate_mean(alpha, sigma_l, sigma_r):
return (sigma_r - sigma_l) * constant * (special.gamma(2 / alpha) / special.gamma(1 / alpha))
alpha = estimate_alpha(x)
sigma_l = estimate_sigma(x, alpha, lambda z: z < 0)
sigma_r = estimate_sigma(x, alpha, lambda z: z >= 0)
constant = np.sqrt(special.gamma(1 / alpha) / special.gamma(3 / alpha))
mean = estimate_mean(alpha, sigma_l, sigma_r)
return alpha, mean, sigma_l, sigma_r
# 计算BRISQUE特征
def calculate_brisque_features(image, kernel_size=7, sigma=7 / 6):
def calculate_features(coefficients_name, coefficients, accum=np.array([])):
alpha, mean, sigma_l, sigma_r = asymmetric_generalized_gaussian_fit(coefficients)
if coefficients_name == 'mscn':
var = (sigma_l ** 2 + sigma_r ** 2) / 2
return [alpha, var]
return [alpha, mean, sigma_l ** 2, sigma_r ** 2]
mscn_coefficients = calculate_mscn_coefficients(image, kernel_size, sigma)
coefficients = calculate_pair_product_coefficients(mscn_coefficients)
features = [calculate_features(name, coeff) for name, coeff in coefficients.items()]
flatten_features = list(chain.from_iterable(features))
return np.array(flatten_features)
# 辅助函数
def load_image(url):
image_stream = request.urlopen(url)
return skimage.io.imread(image_stream, plugin='pil')
def plot_histogram(x, label):
n, bins = np.histogram(x.ravel(), bins=50)
n = n / np.max(n)
plt.plot(bins[:-1], n, label=label, marker='o')
# 在创建计算brisque特征所需的所有函数后,我们可以估计给定图像的图像质量。他们使用来自柯达数据集的图像。
# 1.加载图像
plt.rcParams["figure.figsize"] = 12, 9
url = 'http://www.cs.albany.edu/~xypan/research/img/Kodak/kodim05.png'
image = load_image(url)
gray_image = skimage.color.rgb2gray(image)
_ = skimage.io.imshow(image)
# 2.计算系数
mscn_coefficients = calculate_mscn_coefficients(gray_image, 7, 7 / 6)
coefficients = calculate_pair_product_coefficients(mscn_coefficients)
plt.rcParams["figure.figsize"] = 12, 11
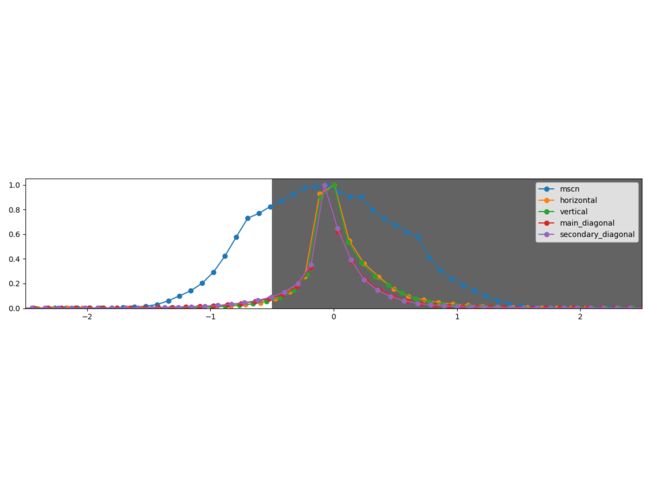
for name, coeff in coefficients.items():
plot_histogram(coeff.ravel(), name)
# 在计算 MSCN 系数和两两相乘后,我们可以验证分布实际上是不同的。
plt.axis([-2.5, 2.5, 0, 1.05])
plt.legend()
plt.show()
# 3. 广义高斯分布的拟合系数
brisque_features = calculate_brisque_features(gray_image, kernel_size=7, sigma=7 / 6)
# 4.调整图像大小并计算 BRISQUE 特征
downscaled_image = cv2.resize(gray_image, None, fx=1 / 2, fy=1 / 2, interpolation=cv2.INTER_CUBIC)
downscale_brisque_features = calculate_brisque_features(downscaled_image, kernel_size=7, sigma=7 / 6)
brisque_features = np.concatenate((brisque_features, downscale_brisque_features))
# 5. 缩放特征并送给 SVR
# 作者提供了一个预训练的 SVR 模型来计算质量评估。然而,
# 为了得到好的结果,我们需要将特征缩放到[- 1,1]。对于后者,我们需要作者用来缩放特征向量的相同参数。
def scale_features(features):
with open('normalize.pickle', 'rb') as handle:
scale_params = pickle.load(handle)
min_ = np.array(scale_params['min_'])
max_ = np.array(scale_params['max_'])
return -1 + (2.0 / (max_ - min_) * (features - min_))
def calculate_image_quality_score(brisque_features):
model = svmutil.svm_load_model('brisque_svm.txt')
scaled_brisque_features = scale_features(brisque_features)
x, idx = svmutil.gen_svm_nodearray(
scaled_brisque_features,
isKernel=(model.param.kernel_type == svmutil.PRECOMPUTED))
nr_classifier = 1
prob_estimates = (svmutil.c_double * nr_classifier)()
return svmutil.libsvm.svm_predict_probability(model, x, prob_estimates)
# 用于表示图像质量的比例从0到100。图像质量为100表示图像的质量很差。
# 在分析图像的情况下,我们得到它是一个高质量的图像。这是有道理的,因为我们使用的是参考图像。
print(calculate_image_quality_score(brisque_features))
# 4.954157281562374
4.1 空间域的自然场景统计(NSS)
给定一幅图像,我们通过原像素减去局部均值然后除以局部偏差,添加一个常数以避免零除法来获得局部归一化的图像。

如 果 I ( i , j ) 域 是 [ 0 , 255 ] 那 么 C = 1 如 果 域 是 [ 0 , 1 ] 那 么 C = 1 / 255 如果 I(i, j) 域是 [0, 255] 那么 C=1 如果域是 [0, 1] 那么 C=1/255 如果I(i,j)域是[0,255]那么C=1如果域是[0,1]那么C=1/255
要计算局部归一化的图像,也称为MSCN系数,我们必须计算局部平均值。这里,w 是大小为 (K, L) 的高斯核。

作者取得局部均值的方式可能有点令人困惑,它是通过对图像应用高斯滤波器来计算的。
def normalize_kernel(kernel):
return kernel / np.sum(kernel)
def gaussian_kernel2d(n, sigma):
Y, X = np.indices((n, n)) - int(n/2)
gaussian_kernel = 1 / (2 * np.pi * sigma ** 2) * np.exp(-(X ** 2 + Y ** 2) / (2 * sigma ** 2))
return normalize_kernel(gaussian_kernel)
def local_mean(image, kernel):
return signal.convolve2d(image, kernel, 'same')
def local_deviation(image, local_mean, kernel):
"Vectorized approximation of local deviation"
sigma = image ** 2
sigma = signal.convolve2d(sigma, kernel, 'same')
return np.sqrt(np.abs(local_mean ** 2 - sigma))
def calculate_mscn_coefficients(image, kernel_size=6, sigma=7/6):
C = 1/255
kernel = gaussian_kernel2d(kernel_size, sigma=sigma)
local_mean = signal.convolve2d(image, kernel, 'same')
local_var = local_deviation(image, local_mean, kernel)
return (image - local_mean) / (local_var + C)
作者发现 MSCN 系数服从广义高斯分布 (GGD) ,适用于更广泛的失真图像。 GGD 密度函数为:

其中,

Г 是 伽 马 函 数 。 参 数 α 控 制 形 状 , σ ² 控 制 方 差 。 Г 是伽马函数。参数 α 控制形状,σ² 控制方差。 Г是伽马函数。参数α控制形状,σ²控制方差。
def generalized_gaussian_dist(x, alpha, sigma):
beta = sigma * np.sqrt(special.gamma(1 / alpha) / special.gamma(3 / alpha))
coefficient = alpha / (2 * beta() * special.gamma(1 / alpha))
return coefficient * np.exp(-(np.abs(x) / beta) ** alpha)
4.2 相邻 MSCN 系数的两两相乘
相邻系数的符号也表现出规则结构,在存在失真时会受到干扰。作者提出了沿四个方向(1)水平H,(2)垂直V,(3)主对角线D1和(4)次对角线D2的相邻MSCN系数的两两相乘模型。

def calculate_pair_product_coefficients(mscn_coefficients):
return collections.OrderedDict({
'mscn': mscn_coefficients,
'horizontal': mscn_coefficients[:, :-1] * mscn_coefficients[:, 1:],
'vertical': mscn_coefficients[:-1, :] * mscn_coefficients[1:, :],
'main_diagonal': mscn_coefficients[:-1, :-1] * mscn_coefficients[1:, 1:],
'secondary_diagonal': mscn_coefficients[1:, :-1] * mscn_coefficients[:-1, 1:]
})
此外,他提到 GGD 不能很好地拟合系数乘积的经验直方图。因此,他们建议拟合非对称广义高斯分布 (AGGD) 模型,而不是将这些系数拟合到 GGD。 AGGD 密度函数为:

其中,

s i d e 可 以 是 r 或 l 。 side 可以是 r 或 l。 side可以是r或l。前面公式中没有体现的另一个参数是均值:

def asymmetric_generalized_gaussian(x, nu, sigma_l, sigma_r):
def beta(sigma):
return sigma * np.sqrt(special.gamma(1 / nu) / special.gamma(3 / nu))
coefficient = nu / ((beta(sigma_l) + beta(sigma_r)) * special.gamma(1 / nu))
f = lambda x, sigma: coefficient * np.exp(-(x / beta(sigma)) ** nu)
return np.where(x < 0, f(-x, sigma_l), f(x, sigma_r))
4.3 拟合非对称广义高斯分布
算法步骤为:
def estimate_phi(alpha):
numerator = special.gamma(2 / alpha) ** 2
denominator = special.gamma(1 / alpha) * special.gamma(3 / alpha)
return numerator / denominator
def estimate_r_hat(x):
size = np.prod(x.shape)
return (np.sum(np.abs(x)) / size) ** 2 / (np.sum(x ** 2) / size)
def estimate_R_hat(r_hat, gamma):
numerator = (gamma ** 3 + 1) * (gamma + 1)
denominator = (gamma ** 2 + 1) ** 2
return r_hat * numerator / denominator
def mean_squares_sum(x, filter = lambda z: z == z):
filtered_values = x[filter(x)]
squares_sum = np.sum(filtered_values ** 2)
return squares_sum / ((filtered_values.shape))
def estimate_gamma(x):
left_squares = mean_squares_sum(x, lambda z: z < 0)
right_squares = mean_squares_sum(x, lambda z: z >= 0)
return np.sqrt(left_squares) / np.sqrt(right_squares)
def estimate_alpha(x):
r_hat = estimate_r_hat(x)
gamma = estimate_gamma(x)
R_hat = estimate_R_hat(r_hat, gamma)
solution = optimize.root(lambda z: estimate_phi(z) - R_hat, [0.2]).x
return solution[0]
def estimate_sigma(x, alpha, filter = lambda z: z < 0):
return np.sqrt(mean_squares_sum(x, filter))
def estimate_mean(alpha, sigma_l, sigma_r):
return (sigma_r - sigma_l) * constant * (special.gamma(2 / alpha) / special.gamma(1 / alpha))
alpha = estimate_alpha(x)
sigma_l = estimate_sigma(x, alpha, lambda z: z < 0)
sigma_r = estimate_sigma(x, alpha, lambda z: z >= 0)
constant = np.sqrt(special.gamma(1 / alpha) / special.gamma(3 / alpha))
mean = estimate_mean(alpha, sigma_l, sigma_r)
return alpha, mean, sigma_l, sigma_r
4.4 计算 BRISQUE 特征
计算图像质量所需的特征是将MSCN系数和移位乘积拟合到广义高斯分布的结果。首先,我们需要将MSCN系数拟合到GDD上,然后将两两乘积拟合到AGGD上。以下是对这些特性的总结:

def calculate_brisque_features(image, kernel_size=7, sigma=7/6):
def calculate_features(coefficients_name, coefficients, accum=np.array([])):
alpha, mean, sigma_l, sigma_r = asymmetric_generalized_gaussian_fit(coefficients)
if coefficients_name == 'mscn':
var = (sigma_l ** 2 + sigma_r ** 2) / 2
return [alpha, var]
return [alpha, mean, sigma_l ** 2, sigma_r ** 2]
mscn_coefficients = calculate_mscn_coefficients(image, kernel_size, sigma)
coefficients = calculate_pair_product_coefficients(mscn_coefficients)
features = [calculate_features(name, coeff) for name, coeff in coefficients.items()]
flatten_features = list(chain.from_iterable(features))
return np.array(flatten_features)
4.5 结果
参考目录
https://towardsdatascience.com/automatic-image-quality-assessment-in-python-391a6be52c11
https://github.com/ocampor/image-quality
https://mp.weixin.qq.com/s/O9t4lTSHjSi044X1ZX0nhQ