Baidu Apollo代码解析之EM Planner中的QP Path Optimizer 3

大家好，我已经把CSDN上的博客迁移到了知乎上，欢迎大家在知乎关注我的专栏慢慢悠悠小马车（https://zhuanlan.zhihu.com/duangduangduang）。希望大家可以多多交流，互相学习。

---

本节主要分析optimization中的kernel，即要优化的目标，其实就是cost function，整体以

的形式呈现，由很多部分组成。在EM Planner的论文中，主要有4部分，如下式。而在GitHub的材料中，只提到了下式的前3部分。代码中则更丰富，有6部分。

 

设定kernel函数，是由QpSplinePathGenerator::AddKernel()实现的。

void QpSplinePathGenerator::AddKernel() {
  Spline1dKernel* spline_kernel = spline_solver_->mutable_spline_kernel();

  if (init_trajectory_point_.v() < qp_spline_path_config_.uturn_speed_limit() &&
      !is_change_lane_path_ &&
      qp_spline_path_config_.reference_line_weight() > 0.0) {
    // 只有在!is_change_lane_path_的情况才会进入，而!is_change_lane_path_会导致ref_l_=0
    std::vector ref_l(evaluated_s_.size(), -ref_l_);
    // 添加和参考线相关的kernel，推测应该是使轨迹尽可能贴近参考线，但我在代码中没有理解这一点
    // 而且每次ref_l元素全是0，会导致函数内offset_全是0，意义何在？
    // 参考线或下面的历史轨迹，可以是DP输出的粗糙规划结果
    spline_kernel->AddReferenceLineKernelMatrix(
        evaluated_s_, ref_l, qp_spline_path_config_.reference_line_weight());
  }

  if (qp_spline_path_config_.history_path_weight() > 0.0) {
    // 添加和历史轨迹相关的kernel，推测应该是使轨迹尽可能近似延续之前的轨迹，但我在代码中没有理解这一点    
    AddHistoryPathKernel();
  }

  if (qp_spline_path_config_.regularization_weight() > 0.0) {
    // 添加正则项
    spline_kernel->AddRegularization(
        qp_spline_path_config_.regularization_weight());
  }

  if (qp_spline_path_config_.derivative_weight() > 0.0) {
    // 添加1阶导kernel，(f'(x))^2积分
    spline_kernel->AddDerivativeKernelMatrix(
        qp_spline_path_config_.derivative_weight());
    if (std::fabs(init_frenet_point_.l()) >
        qp_spline_path_config_.lane_change_mid_l()) {
      spline_kernel->AddDerivativeKernelMatrixForSplineK(
          0, qp_spline_path_config_.first_spline_weight_factor() *
                 qp_spline_path_config_.derivative_weight());
    }
  }

  if (qp_spline_path_config_.second_derivative_weight() > 0.0) {
    // 添加2阶导kernel，(f''(x))^2积分
    spline_kernel->AddSecondOrderDerivativeMatrix(
        qp_spline_path_config_.second_derivative_weight());
    if (std::fabs(init_frenet_point_.l()) >
        qp_spline_path_config_.lane_change_mid_l()) {
      spline_kernel->AddSecondOrderDerivativeMatrixForSplineK(
          0, qp_spline_path_config_.first_spline_weight_factor() *
                 qp_spline_path_config_.second_derivative_weight());
    }
  }

  if (qp_spline_path_config_.third_derivative_weight() > 0.0) {
    // 添加3阶导kernel，(f'''(x))^2积分
    spline_kernel->AddThirdOrderDerivativeMatrix(
        qp_spline_path_config_.third_derivative_weight());
    if (std::fabs(init_frenet_point_.l()) >
        qp_spline_path_config_.lane_change_mid_l()) {
      spline_kernel->AddThirdOrderDerivativeMatrixForSplineK(
          0, qp_spline_path_config_.first_spline_weight_factor() *
                 qp_spline_path_config_.third_derivative_weight());
    }
  }
}

AddReferenceLineKernelMatrix()，AddHistoryPathKernel()和AddRegularization()理解的不透彻，先不介绍了。以添加1阶导kernel为例，GitHub上的材料详细的展示了计算kernel的过程，将 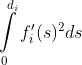的形式转换为

AddDerivativeKernelMatrix()便是构造中间矩阵的过程，我认为这就是（0）式中的H。参考

void Spline1dKernel::AddDerivativeKernelMatrix(const double weight) {
  AddNthDerivativekernelMatrix(1, weight);
}

void Spline1dKernel::AddNthDerivativekernelMatrix(const uint32_t n,
                                                  const double weight) {
  const uint32_t num_params = spline_order_ + 1;
  for (uint32_t i = 0; i + 1 < x_knots_.size(); ++i) {
    // weight是公式中的权重，2不理解，对于所有的cost项都×2，相当于没有影响
    Eigen::MatrixXd cur_kernel = 2 *
        SplineSegKernel::Instance()->NthDerivativeKernel(
            n, num_params, x_knots_[i + 1] - x_knots_[i]) * weight;
    kernel_matrix_.block(i * num_params, i * num_params, num_params,
                         num_params) += cur_kernel;
  }
}

Eigen::MatrixXd SplineSegKernel::NthDerivativeKernel(
    const uint32_t n, const uint32_t num_params, const double accumulated_x) {
  if (n == 1) {
    return DerivativeKernel(num_params, accumulated_x);
  }
  ...
}

Eigen::MatrixXd SplineSegKernel::DerivativeKernel(const uint32_t num_params,
                                                  const double accumulated_x) {
  // reserved_order_初始化为5，对于常用的3次、5次多项式，CalculateDerivative()不会执行                               
  if (num_params > reserved_order_ + 1) {
    CalculateDerivative(num_params);
  }
  Eigen::MatrixXd term_matrix;
  IntegratedTermMatrix(num_params, accumulated_x, "derivative", &term_matrix);
  //cwiseProduct是对应元素逐一相乘
  return kernel_derivative_.block(0, 0, num_params, num_params)
      .cwiseProduct(term_matrix);
}

DerivativeKernel()的返回值，便是上述（1）式的中间矩阵。kernel_derivative_在SplineSegKernel的构造函数中初始化，其实是中间矩阵的分数部分，而IntegratedTermMatrix()计算的term_matrix，则是中间矩阵的幂部分，通过cwiseProduct()相乘得到中间矩阵。

SplineSegKernel::SplineSegKernel() {
  const int reserved_num_params = reserved_order_ + 1;
  CalculateFx(reserved_num_params);
  CalculateDerivative(reserved_num_params);
  CalculateSecondOrderDerivative(reserved_num_params);
  CalculateThirdOrderDerivative(reserved_num_params);
}

void SplineSegKernel::CalculateDerivative(const uint32_t num_params) {
  kernel_derivative_ = Eigen::MatrixXd::Zero(num_params, num_params);
  for (int r = 1; r < kernel_derivative_.rows(); ++r) {
    for (int c = 1; c < kernel_derivative_.cols(); ++c) {
      kernel_derivative_(r, c) = r * c / (r + c - 1.0);
    }
  }
}

void SplineSegKernel::IntegratedTermMatrix(const uint32_t num_params,
                                           const double x,
                                           const std::string& type,
                                           Eigen::MatrixXd* term_matrix) const {
  ...
  std::vector x_pow(2 * num_params + 1, 1.0);
  for (uint32_t i = 1; i < 2 * num_params + 1; ++i) {
    x_pow[i] = x_pow[i - 1] * x;
  }
  ...
  } else if (type == "derivative") {
    for (uint32_t r = 1; r < num_params; ++r) {
      for (uint32_t c = 1; c < num_params; ++c) {
        (*term_matrix)(r, c) = x_pow[r + c - 1];
      }
    }
    (*term_matrix).block(0, 0, num_params, 1) =
        Eigen::MatrixXd::Zero(num_params, 1);
    (*term_matrix).block(0, 0, 1, num_params) =
        Eigen::MatrixXd::Zero(1, num_params);

  }
  ...
}

逐项计算cost后，都保存入Spline1dKernel::kernel_matrix_变量中，其初始化为（spline个数）×（spline阶数+1）维矩阵。

Spline1dKernel::Spline1dKernel(const std::vector& x_knots,
                               const uint32_t spline_order)
    : x_knots_(x_knots), spline_order_(spline_order) {
  //所有curve方程的参数个数
  total_params_ =
      (static_cast(x_knots.size()) > 1
           ? (static_cast(x_knots.size()) - 1) * (1 + spline_order_)
           : 0);
  kernel_matrix_ = Eigen::MatrixXd::Zero(total_params_, total_params_);
  offset_ = Eigen::MatrixXd::Zero(total_params_, 1);
}

由AddNthDerivativekernelMatrix()中kernel_matrix_更新元素的方式，我们可以看出kernel_matrix_一定是下面这种形式，n = spline order + 1，每一个n*n矩阵都对应着一段spline。

AddKernel()中，如果处在变道的过程中，则添加一项额外的cost，并且只作用于第一段spline。AddDerivativeKernelMatrixForSplineK()与AddDerivativeKernelMatrix()如出一辙，唯一的区别是因为针对特定段的spline，没有对knots的循环。最底层同样都是调用SplineSegKernel::Instance()->NthDerivativeKernel()实现的。

void Spline1dKernel::AddNthDerivativekernelMatrixForSplineK(
    const uint32_t n, const uint32_t k, const double weight) {
  ...
  const uint32_t num_params = spline_order_ + 1;
  Eigen::MatrixXd cur_kernel = 2 *
      SplineSegKernel::Instance()->NthDerivativeKernel(
          n, num_params, x_knots_[k + 1] - x_knots_[k]) * weight;
  kernel_matrix_.block(k * num_params, k * num_params, num_params,
                       num_params) += cur_kernel;
}

至此，QP Optimization的目标函数和约束都设定好了，接下来就是优化求解了。