EM规划器:EMPlanner
EM规划器:EMPlanner
EM规划器,也是规划模块Planning的核心,主要的任务是根据:
- 感知模块Perception和预测模块Prediction得到的障碍物以及未来时间(e.g. 5s内)的运动轨迹
- 当前路况,禁停区、减速带、停车标志、人行横道等等
来最终规划无人车的最优行驶路径。从参考线提供器ReferenceLineProvider可以看到,当无人车面临变道时,就会存在多条参考线(变道时间可随机扰动,变道早可能进入车道1,变道晚就可能进入车道2)。那么EM规划器就需要计算每条参考线上的最优行驶路径,最后进行综合,得到开销(也就是cost)最小的一条路径。EM规划器对无人车的控制规划进行拆分,分为2类:
- 路径规划(也就是行驶位置, path-time)
- 速度规划(speed)
那么对于路径规划和速度规划,可以有两种方法,分别为:
- 动态规划(dynamic programming)
- 二次规划(quadratic programming + Spline interpolation,这个和参考线平滑很相似)
上述两种规划方案,Apollo采用的是第一种动态规划法,这种方法的原理很简单,我们这里以速度规划为例,进行简单的流程简述:
step 1:初始化规划起点,可以是车辆当前坐标。然后每隔一段距离(例如10m)规划一次位置,一共向前规划如40m。
step 2:在下个位置侧向进行一些点采样(例如7个),也就是计算在车道不同宽度位置采样。然后计算每个采样点到前一层所有点的cost,就可以得到其实规划点到当前采样点的最短路径与开销cost。
step 3:前进到最小cost对应的采样点,然后重复2对下个位置横向采样并计算开销cost。最终从终点开始,反向选择一条cost最小的路径。
使用数学的形式来表示,进一步理解动态规划的思想。假设规划起始点为s,需要向前规划M米,那么可以每个d米进行一次采样(也就是纵向采样),每次采样位置可以横向选择若干个点(横向采样),表示无人车可以前进到这个车道宽度位置,最终找到一条从起始点到终点的最优行驶路径。
为了更加生动形象的理解,我们以神经网络为类比模型。规划起始点s就是神经网络的输入,只有一个点;规划终止点x其实就是神经网络的输出,但是可以有若干点,这些点在参考线上的长度一致,但车道宽度可以不一致,也就是说可以规划到路中央,也可以规划到路边。纵向每隔d米采样其实就是类似于一个个隐藏层,每个位置横向采样就是该隐藏层的不同神经元。网络中相邻层之间神经元的连接权值就是从前一个点行驶到另一个点所需要的开销cost。那么计算一条最优路径path(s)可以表示为:
m i n c o s t ( p a t h ( s , x l ) ) = m i n i m i n j ( m i n c o s t ( p a t h ( a , x j l − 1 ) ) + c o s t ( x j l − 1 , x i l ) ) mincost(path(s,x^l)) = min_i min_j (mincost(path(a,x_j^{l-1})) + cost(x_j^{l-1}, x_i^{l})) mincost(path(s,xl))=miniminj(mincost(path(a,xjl−1))+cost(xjl−1,xil))
公式中$ mincost(path(s,x^l)) 表 示 从 规 划 起 始 点 s 到 规 划 终 点 ( 也 就 是 l e v e l 层 输 出 的 最 小 开 销 ) , 只 需 要 取 输 出 层 中 具 有 最 小 开 销 的 点 即 可 , 也 就 对 应 表示从规划起始点s到规划终点(也就是level层输出的最小开销),只需要取输出层中具有最小开销的点即可,也就对应 表示从规划起始点s到规划终点(也就是level层输出的最小开销),只需要取输出层中具有最小开销的点即可,也就对应min_i$,其中i从0开始到输出层的数量。起始点到终点i个神经元的最小开销,可以分别计算起始点到倒数第二层每个神经元的最小开销 m i n c o s t ( p a t h ( a , x j l − 1 ) ) mincost(path(a,x_j^{l-1})) mincost(path(a,xjl−1)),在加上这个神经元到终点i神经元的开销 c o s t ( x j l − 1 , x i l ) cost(x_j^{l-1}, x_i^{l}) cost(xjl−1,xil),最后取倒数第二层中j个神经元计算最小值,即为整个最优路径的cost,这就是动态规划的原理。神经网络中每个点都保存着起始点到该点的最小开销cost,也就是 m i n c o s t ( p a t h ( a , b ) mincost(path(a,b) mincost(path(a,b)。
在计算开销cost的过程中,需要考略三个因素:无人车位置(最好就是验证参考线前进,横向不停地调整会增加cost),静态障碍物以及动态障碍物(这两类已经在Frame中完成设置,已经考虑到感知物体和路况)。
下面我们就对路径规划和速度规划做一个详细的了解。代码中使用了动态规划法对路径进行规划;同时使用动态规划与二次规划+样条线插值对速度进行规划
planner_type : EM
em_planner_config {
task : DP_POLY_PATH_OPTIMIZER
task : PATH_DECIDER
task : DP_ST_SPEED_OPTIMIZER
task : SPEED_DECIDER
task : QP_SPLINE_ST_SPEED_OPTIMIZER
}
路径规划器–DpPolyPathOptimizer
先看一下代码结构:
/// file in apollo/modules/planning/planner/em/em_planner.cc
Status EMPlanner::Plan(const TrajectoryPoint& planning_start_point, Frame* frame) {
for (auto& reference_line_info : frame->reference_line_info()) { // 先分别对每条参考线进行规划
auto cur_status = PlanOnReferenceLine(planning_start_point, frame, &reference_line_info); // 规划主函数
}
Status EMPlanner::PlanOnReferenceLine(
const TrajectoryPoint& planning_start_point, Frame* frame,
ReferenceLineInfo* reference_line_info) {
for (auto& optimizer : tasks_) { // 对每条参考线分别进行所有任务的规划,包括速度规划、路径位置规划、位置决策器规划等。
ret = optimizer->Execute(frame, reference_line_info);
}
}
/// file in apollo/modules/planning/tasks/path_optimizer.cc
apollo::common::Status PathOptimizer::Execute(Frame* frame, ReferenceLineInfo* const reference_line_info) {
Task::Execute(frame, reference_line_info);
auto ret = Process( // 最终会调用路径规划类的Process函数
reference_line_info->speed_data(), reference_line_info->reference_line(),
frame->PlanningStartPoint(), reference_line_info->mutable_path_data());
return ret;
}
/// file in apollo/planning/tasks/dp_poly_path/dp_poly_path_optimizer.cc
Status DpPolyPathOptimizer::Process(const SpeedData &speed_data,
const ReferenceLine &,
const common::TrajectoryPoint &init_point,
PathData *const path_data) {
DPRoadGraph dp_road_graph(config_, *reference_line_info_, speed_data);
if (!dp_road_graph.FindPathTunnel( // 寻找参考线最优的行驶路径,由DPRoadGraph::FindPathTunnel完成。
init_point,
reference_line_info_->path_decision()->path_obstacles().Items(),
path_data)) {
...
}
}
从上面的代码结构,可以进一步验证开始我们的想法,规划的方法是先独立对所有参考线进行单独规划,每条参考线可以得到一个最优的行进路线;最后综合所有参考线的最优行进路线,选择"全局"最优的路线。下面就对DPRoadGraph::FindPathTunnel函数进行解析,大体的逻辑也很简单,主要分3步:
Step A. 计算起始点的累计距离s,侧方相对偏移l,侧向速度dl和侧向速度ddl
Step B. 获取当前参考线下最优的前进路线
Step C. 将最优前进路线封装成path_data
/// file in apollo/modules/planning/tasks/dp_poly_path/dp_road_graph.cc
bool DPRoadGraph::FindPathTunnel(
const common::TrajectoryPoint &init_point,
const std::vector &obstacles,
PathData *const path_data) {
// Step A. 计算起始点的累计距离s,侧方相对偏移l,侧向速度dl和侧向速度ddl
if (!CalculateFrenetPoint(init_point_, &init_frenet_frame_point_)) {
return false;
}
// Step B. 获取当前参考线下最优的前进路线
std::vector min_cost_path;
if (!GenerateMinCostPath(obstacles, &min_cost_path)) {
return false;
}
// Step C. 将最优前进路线封装成path_data
std::vector frenet_path;
for (std::size_t i = 1; i < min_cost_path.size(); ++i) {
...
}
FrenetFramePath tunnel(frenet_path);
path_data->SetReferenceLine(&reference_line_);
path_data->SetFrenetPath(tunnel);
return true;
}
步骤A和C没什么难点,B步骤稍微有点繁琐,下面我们将逐步进行分析。在计算当前参考线下最优的前进路线时,正如开始所说的,可以每隔一段距离,就在车道横向采样一些点,表示无人车在车道不同宽度行驶时坐标,然后计算两个距离之间cost最小的坐标对,这就代表当前位置到下一位置的最优路径。这样就需要一步步解决以下问题:
Q1:如何采样坐标点?–SamplePathWaypoints函数
这个问题在开始已经说过,规划首先就需要考虑:
- 规划未来多久的距离?
答案是未来近40m的距离,可以通过观察代码:
const float kMinSampleDistance = 40.0;
const float total_length = std::fmin(
init_sl_point_.s() + std::fmax(init_point.v() * 8.0, kMinSampleDistance),
reference_line_.Length());
具体还需要考虑规划起始点的无人车速度以及参考线的长度。
- 每隔多久进行一次采样(纵向采样)?每次采样车道横向不同位置采样几个点(横向采样)?
答案也比较简单,大约每个10-20m,对车道不同宽度进行采样。
const size_t num_sample_per_level = // 每个位置,横向采样7个点
FLAGS_use_navigation_mode ? config_.navigator_sample_num_each_level() // navigator_sample_num_each_level: 3
: config_.sample_points_num_each_level(); // sample_points_num_each_level: 7
const bool has_sidepass = HasSidepass();
constexpr float kSamplePointLookForwardTime = 4.0;
const float step_length = // 将step_length裁剪到[20,40]米之间
common::math::Clamp(init_point.v() * kSamplePointLookForwardTime,
config_.step_length_min(), config_.step_length_max());
const float level_distance = // 每隔level_distance进行一次横向采样,纵向采样的间隔差不多10-20m
(init_point.v() > FLAGS_max_stop_speed) ? step_length : step_length / 2.0;
float accumulated_s = init_sl_point_.s();
float prev_s = accumulated_s;
上面代码有一个词–level,其实就是纵向采样点,每个level中会横向采样若干点。当然,可以更紧凑的纵向与横向采样,但是在计算cost会增加过大的计算量,所以需要经过权衡。
- 纵向&&横向怎么样进行采样?
首先如果无人车当前状态正在寻找停车点,也就是PULL_OVER状态,那么采样点其实只要设置为PULL_OVER的计算得到的起始点即可,当前前提条件是需要进入到他的可操作区域。
if (status->planning_state().has_pull_over() &&
status->planning_state().pull_over().in_pull_over()) {
status->mutable_planning_state()->mutable_pull_over()->set_status(
PullOverStatus::IN_OPERATION);
if (init_sl_point_.s() > start_point_sl.s()) { // 表示无人车已进入PULL_OVER可操作区域
const auto &stop_point = status->planning_state().pull_over().stop_point();
SLPoint stop_point_sl;
if (!reference_line_.XYToSL(stop_point, &stop_point_sl)) {
AERROR << "Fail to change xy to sl.";
return false;
}
std::vector level_points(1, stop_point_sl); // 这时候只要设置停车点为下一时刻(纵向)的采样点即可,那么横向采样点就只有一个,就是停车位置
points->emplace_back(level_points);
return true;
}
}
然后循环进行纵向+横向采样,
for (std::size_t i = 0; accumulated_s < total_length; ++i) {
accumulated_s += level_distance;
// 计算纵向每个位置,有效的左右边界,kBoundaryBuff是无人车与车道线边界线的间距。需要保持无人车在车道内行驶。
reference_line_.GetLaneWidth(s, &left_width, &right_width);
constexpr float kBoundaryBuff = 0.20;
const float eff_right_width = right_width - half_adc_width - kBoundaryBuff; // 计算右有效宽度
const float eff_left_width = left_width - half_adc_width - kBoundaryBuff; // 计算左有效宽度
float kDefaultUnitL = 1.2 / (num_sample_per_level - 1); // 每个位置上横向采样时,采样点之间的距离,差不多0.2m
if (reference_line_info_.IsChangeLanePath() && // 如果当前参考线是变道,且变道不安全(无人车前后一定距离内有障碍物)
!reference_line_info_.IsSafeToChangeLane()) { // ,那么增加采样点间隔,这样可以下一时刻减少变道的时间。
kDefaultUnitL = 1.0;
}
const float sample_l_range = kDefaultUnitL * (num_sample_per_level - 1); // 横向采样的宽度
float sample_right_boundary = -eff_right_width; // 计算FLU坐标系下,右边界
float sample_left_boundary = eff_left_width; // 计算FLU坐标系下,左边界
const float kLargeDeviationL = 1.75;
if (reference_line_info_.IsChangeLanePath() || // 修正左右边界,如果参考线需要变道,并且已经便宜车道了,那么就将横向采样区间向变道方向平移。
std::fabs(init_sl_point_.l()) > kLargeDeviationL) {
sample_right_boundary = std::fmin(-eff_right_width, init_sl_point_.l()); // 左变道,修正左边界
sample_left_boundary = std::fmax(eff_left_width, init_sl_point_.l()); // 右变道,修正右边界
if (init_sl_point_.l() > eff_left_width) { // 左变道,修正右边界,向左平移,因为左变道车道线右边的区域不用考虑
sample_right_boundary = std::fmax(sample_right_boundary, init_sl_point_.l() - sample_l_range);
}
if (init_sl_point_.l() < eff_right_width) { // 右变道,修正左边界,向右平移,因为右变道车道线左边的区域不用考虑
sample_left_boundary = std::fmin(sample_left_boundary, init_sl_point_.l() + sample_l_range);
}
}
// 具体采样
...
}
最后进行每个纵向位置的横向区间采样,采样分两个多类情况:
情况1:如果当前参考线需要变道,并且变道不安全,那么横向采样点就设置为第二条参考线的位置,直接走第二条参考线。
if (reference_line_info_.IsChangeLanePath() &&
!reference_line_info_.IsSafeToChangeLane()) {
sample_l.push_back(reference_line_info_.OffsetToOtherReferenceLine());
}
情况2:如果当前参考线需要侧方绕行(SIDEPASS),即从旁边超车。若是可以进行左边超车,那么横向采样点设置为左边界+超车距离;右边超车,横向采样点设置为右边界+超车距离
else if (has_sidepass) {
// currently only left nudge is supported. Need road hard boundary for
// both sides
switch (sidepass_.type()) {
case ObjectSidePass::LEFT: {
sample_l.push_back(eff_left_width + config_.sidepass_distance());
break;
}
case ObjectSidePass::RIGHT: {
sample_l.push_back(-eff_right_width - config_.sidepass_distance());
break;
}
default:
break;
}
}
情况3:正常行驶情况下,从横向区间[sample_right_boundary , sample_left_boundary]大小为sample_l_range进行均匀采样
else {
common::util::uniform_slice(sample_right_boundary, sample_left_boundary,
num_sample_per_level - 1, &sample_l);
}
计算每个横向采样点的相对偏移距离l和累计距离s,封装成一个level,最后所有level封装成way_points
for (std::size_t i = 0; accumulated_s < total_length; ++i) { // 纵向采样
std::vector level_points;
planning_internal::SampleLayerDebug sample_layer_debug;
for (size_t j = 0; j < sample_l.size(); ++j) { // 每个纵向位置采样得到的所有横向采样点,封装成一个level
common::SLPoint sl = common::util::MakeSLPoint(s, sample_l[j]);
sample_layer_debug.add_sl_point()->CopyFrom(sl);
level_points.push_back(std::move(sl));
}
if (!reference_line_info_.IsChangeLanePath() && has_sidepass) { // 对于不变道但是要超车的情况,额外增加一个车道线中心采样点
auto sl_zero = common::util::MakeSLPoint(s, 0.0);
level_points.push_back(std::move(sl_zero));
}
if (!level_points.empty()) { // level不为空,封装进最终的way+points
points->emplace_back(level_points);
}
Q2:如何计算两个level之间两两横向采样点之间的开销?–UpdateNode函数和TrajectoryCost类
一个注意点,Q1中采样其实没有把规划起始点加进去,代码中做了一个修正。
path_waypoints.insert(path_waypoints.begin(), std::vector{init_sl_point_});
- 障碍物处理
在规划中,需要考虑到障碍物的轨迹信息,也就是需要考虑未来每个时刻,障碍物出现的位置,只要将障碍物每个时间点出现的位置,作为开销计算项即可。
TrajectoryCost trajectory_cost(
config_, reference_line_, reference_line_info_.IsChangeLanePath(),
obstacles, vehicle_config.vehicle_param(), speed_data_, init_sl_point_);
未来每个时间点计算方法也很简单:
const float total_time = std::min(heuristic_speed_data_.TotalTime(), FLAGS_prediction_total_time);
num_of_time_stamps_ = static_cast(std::floor(total_time / config.eval_time_interval()));
上述FLAGS_prediction_total_time其实就是PRediction模块中障碍物轨迹预测总时间,5s。eval_time_interval其实就是Prediction模块中障碍物两个预测轨迹点的时间差,0.1s。所以一共差不多50个位置点。最后对参考线上的每个障碍物在每个时间点设定位置标定框。
对于每个障碍物,进行如下条件判断:
情况1:如果是无人车可忽略的障碍物或者迫使无人车停车的障碍物,就不需要考虑。因为前者对无人车前进无影响;后者情况无人车智能停车,根本不需要前进了。
情况2:如果无人车和某个时间点的障碍物横向距离比较大,那么无人车可以毫无影响的前进,所以该类障碍物也可以忽略。
情况3:如果障碍物是虚拟障碍物,那么无人车可以毫无影响的前进,所以该类障碍物也可以忽略。
情况4:如果障碍物是静止的,那么将其加入静止障碍物队列
情况5:如果障碍物时运动的,那么就需要计算障碍物在该时间点的位置,并将其加入动态障碍物队列
std::vector box_by_time;
for (uint32_t t = 0; t <= num_of_time_stamps_; ++t) { // 计算每个时间点的位置,转换成标定框加入动态障碍物队列
TrajectoryPoint trajectory_point =
ptr_obstacle->GetPointAtTime(t * config.eval_time_interval());
Box2d obstacle_box = ptr_obstacle->GetBoundingBox(trajectory_point);
constexpr float kBuff = 0.5;
Box2d expanded_obstacle_box =
Box2d(obstacle_box.center(), obstacle_box.heading(),
obstacle_box.length() + kBuff, obstacle_box.width() + kBuff);
box_by_time.push_back(expanded_obstacle_box);
}
dynamic_obstacle_boxes_.push_back(std::move(box_by_time));
- level之间两两计算cost
bool DPRoadGraph::GenerateMinCostPath(
std::list> graph_nodes; // 这是最后的前向遍历图,类似于神经网络结构,N个level,每个level若干横向采样点,两层level之间的采样点互相连接。
graph_nodes.emplace_back(); // 而且网络中的每个node,都保存了,从规划起始点到该节点的最小cost,以及反向连接链(cost最小对应的parent)
graph_nodes.back().emplace_back(init_sl_point_, nullptr, ComparableCost()); // 输入层(规划起始点)加入网络图
auto &front = graph_nodes.front().front(); // 规划起始点:init_point
size_t total_level = path_waypoints.size(); // 网络层数,level数量
for (std::size_t level = 1; level < path_waypoints.size(); ++level) { // 网络两两level之间计算连接cost
const auto &prev_dp_nodes = graph_nodes.back(); // 前一层level
const auto &level_points = path_waypoints[level]; // 当前层level中的所有横向采样点(类似神经元)
graph_nodes.emplace_back();
for (size_t i = 0; i < level_points.size(); ++i) { // 计算当前层level中与前一层所有计算的连接权值,也就是cost
const auto &cur_point = level_points[i];
graph_nodes.back().emplace_back(cur_point, nullptr);
auto &cur_node = graph_nodes.back().back();
if (FLAGS_enable_multi_thread_in_dp_poly_path) {
...
} else { // 计算前一层prev_dp_nodes和当前层的节点cur_node的开销cost,取prev_dp_nodes中与cur_node开销cost最小的节点,设置为最优路径
UpdateNode(prev_dp_nodes, level, total_level, &trajectory_cost, &front, &cur_node);
}
}
}
}
经过注释,可以很容易的理解整个网络神经元(节点)之间连接cost的流程,那么Update函数中,如何计算前一层和当前层的某个节点之间的开销。其实比较简单,举个例子。现有:
a. 前一层prev_dp_nodes中的某个节点prev_dp_node,它有4个属性:累计距离s0,横向偏移距离l0,横向速度dl0,横向加速度ddl0。
b. 当前层某个节点cur_node,同样4个属性:累计距离s1,横向偏移距离l1,横向速度dl1,横向加速度ddl1。
两个节点之间累积距离就是上述提到level_distance,大约10-20m。那么接下来的工作就是个参考线平滑一样,使用六次多项式进行两个点之间的多项式拟合,y=f(s),自变量是累计距离差s,因变量是横向便宜距离l。经过定义两个点可以数值化为:
prev_dp_node:
l0 = f(0) = prev_dp_node.sl_point.l()
dl0 = f’(0)
ddl0 = f’’(0)
cur_node:
delta_s = cur_node.cur_point.s() - prev_dp_node.prev_sl_point.s()
l1 = f(delta_s) = cur_node.cur_point.l()
dl1 = f’(delta_s) = 0
ddl1 = f’’(delta_s) = 0
匹配过程与Prediction障碍物轨迹预测
那么cur_node与prev_dp_node相连得到的cost为:
const auto cost = trajectory_cost->Calculate(curve, prev_sl_point.s(), cur_point.s(),
level, total_level) + prev_dp_node.min_cost;
cur_node->UpdateCost(&prev_dp_node, curve, cost);
其中UpdateCost是刷新最小cost,这样可以得到与cur_node相连最小的cost,以及对应的prev_dp_node。
最后一个问题:计算开销需要分为哪几项?
Q3:两两node之间的cost如何计算?包含多少项?
正如开头所说,两两level中不同node之间cost计算分为三个部分:路径开销PathCost,静态障碍物开销StaticObstacleCost和动态障碍物开销DynamicObstacleCost,从代码中我们可以清晰的开导cost的组成。
/// file in apollo/modules/planning/tasks/dp_poly_path/trajectory_cost.cc
ComparableCost TrajectoryCost::Calculate(const QuinticPolynomialCurve1d &curve,
const float start_s, const float end_s,
const uint32_t curr_level,
const uint32_t total_level) {
ComparableCost total_cost;
// path cost
total_cost += CalculatePathCost(curve, start_s, end_s, curr_level, total_level);
// static obstacle cost
total_cost += CalculateStaticObstacleCost(curve, start_s, end_s);
// dynamic obstacle cost
total_cost += CalculateDynamicObstacleCost(curve, start_s, end_s);
return total_cost;
}
- 路径开销PathCost
在Q2中已经拟合出了一条前一个node到后一个node的5次多项式,这就是前进的路线中侧方距离l的轨迹。路径开销需要对这条轨迹做评估,具体的评估方法也比较简单。我们已经可以的知道两个node之间的前进距离level_distance大约为10-20米,也就是函数的区间长度为10-20米,我们只需要对区间进行采样,每1米采样一个点,就可以得到约10-20个路径点的侧方距离l,侧方速度dl以及侧方加速度ddl数据。再对这若干组数据评估cost相加即为这条path的开销。
ComparableCost TrajectoryCost::CalculatePathCost(
const QuinticPolynomialCurve1d &curve, const float start_s,
const float end_s, const uint32_t curr_level, const uint32_t total_level) {
for (float curve_s = 0.0; curve_s < (end_s - start_s); curve_s += config_.path_resolution()) { // path_resolution: 1.0m,每1m采样一个点
const float l = curve.Evaluate(0, curve_s); // 根据拟合的5次多项式,计算该点的侧方距离
path_cost += l * l * config_.path_l_cost() * quasi_softmax(std::fabs(l)); // A. 侧方距离l开销,path_l_cost:6.5
double left_width = 0.0;
double right_width = 0.0;
reference_line_->GetLaneWidth(curve_s + start_s, &left_width, &right_width);
constexpr float kBuff = 0.2;
if (!is_change_lane_path_ && (l + width / 2.0 + kBuff > left_width || // 确认是否已经偏离参考线
l - width / 2.0 - kBuff < -right_width)) {
cost.cost_items[ComparableCost::OUT_OF_BOUNDARY] = true;
}
const float dl = std::fabs(curve.Evaluate(1, curve_s));
path_cost += dl * dl * config_.path_dl_cost(); // B. 侧方速度开销,path_dl_cost:8000
const float ddl = std::fabs(curve.Evaluate(2, curve_s));
path_cost += ddl * ddl * config_.path_ddl_cost(); // C. 侧方加速度开销,path_ddl_cost:5
}
if (curr_level == total_level) {
const float end_l = curve.Evaluate(0, end_s - start_s);
path_cost += std::sqrt(end_l - init_sl_point_.l() / 2.0) * config_.path_end_l_cost(); // path_end_l_cost:10000
}
cost.smoothness_cost = path_cost;
}
从代码中可以看到这三部分开销,仔细分析一下可以得到如下结论:
结论1:无论是l,dl和ddl哪个开销,数值越大,cost也就越大。这也表明,Apollo其实鼓励无人车沿着参考线前进,因为沿着参考线前进,l,dl和ddl都是为0的。
结论2:从开销系数来看,Apollo对于侧方距离l和侧方加速度ddl相对来说比较宽松,对侧方速度限制极为严格。但是需要注意一点,但从系数其实无法正确的得到这个结论,因为还要看三者对应的数值范围,如果数值范围小,同时参数小,那么这一项很容易就被忽略了,为了解决这个问题,可以提升其系数,增加权重。
结论3:代码额外增加了起始点和规划终点的侧方偏移,保证不必要的偏移,正常不变道情况下最好是沿着同一车道前进,不变道。
- 静态障碍物开销StaticObstacleCost
ComparableCost TrajectoryCost::CalculateStaticObstacleCost(
const QuinticPolynomialCurve1d &curve, const float start_s,
const float end_s) {
ComparableCost obstacle_cost;
for (float curr_s = start_s; curr_s <= end_s; curr_s += config_.path_resolution()) { // 拟合曲线采样
const float curr_l = curve.Evaluate(0, curr_s - start_s);
for (const auto &obs_sl_boundary : static_obstacle_sl_boundaries_) {
obstacle_cost += GetCostFromObsSL(curr_s, curr_l, obs_sl_boundary);
}
}
obstacle_cost.safety_cost *= config_.path_resolution();
return obstacle_cost;
}
静态障碍物开销其实思路和路径开销一样,在这条多项式曲线上采样,计算每个采样点和所有障碍物的标定框是否重叠,重叠cost就比较大。分情况:
情况1:障碍物和无人车侧方向上的距离大于一个阈值(lateral_ignore_buffer,默认3m),那么cost就是0,忽略障碍物
情况2:如果障碍物在无人车后方,cost为0,可忽略。
否则就计算cost
const float delta_l = std::fabs( // 静态障碍物中心和无人车中心侧方向上的距离
adc_l - (obs_sl_boundary.start_l() + obs_sl_boundary.end_l()) / 2.0);
obstacle_cost.safety_cost += // A. 侧方向距离造成的cost
config_.obstacle_collision_cost() * // 系数,obstacle_collision_cost:1e8
Sigmoid(config_.obstacle_collision_distance() - delta_l); // obstacle_collision_distance:0.5
const float delta_s = std::fabs( // 静态障碍物中心和无人车中心前方向上的距离
adc_s - (obs_sl_boundary.start_s() + obs_sl_boundary.end_s()) / 2.0);
obstacle_cost.safety_cost += // B. 前方向距离造成的cost
config_.obstacle_collision_cost() * // obstacle_collision_cost: 1e8
Sigmoid(config_.obstacle_collision_distance() - delta_s);
那么经过分析就可以得到两个结论:
结论1:静态障碍物cost计算就分为侧方向cost和前方向cost,计算方法是一样的
结论2:从两个方向计算的方法来看,我们可以看到Sigmoid(·)这个函数是单调递减的,在0.5(obstacle_collision_distance)时取0.5,越大取值越小。所以Apollo鼓励无人车在侧方向和前方向上与障碍物保持一定距离,如0.5m以上。
- 动态障碍物开销DynamicObstacleCost
ComparableCost TrajectoryCost::CalculateDynamicObstacleCost(
const QuinticPolynomialCurve1d &curve, const float start_s,
const float end_s) const {
ComparableCost obstacle_cost;
float time_stamp = 0.0;
for (size_t index = 0; index < num_of_time_stamps_; // 障碍物每隔eval_time_interval(默认0.1s)会得到一个运动坐标,分别计算对所有时间点坐标的cost
++index, time_stamp += config_.eval_time_interval()) {
common::SpeedPoint speed_point;
heuristic_speed_data_.EvaluateByTime(time_stamp, &speed_point);
float ref_s = speed_point.s() + init_sl_point_.s();
for (const auto &obstacle_trajectory : dynamic_obstacle_boxes_) { // 对所有动态障碍物分别计算cost
obstacle_cost += GetCostBetweenObsBoxes(ego_box, obstacle_trajectory.at(index));
}
}
constexpr float kDynamicObsWeight = 1e-6;
obstacle_cost.safety_cost *= (config_.eval_time_interval() * kDynamicObsWeight);
return obstacle_cost;
}
区别静态障碍物,动态障碍物会在这个时间段内运动,在前面我们已经对障碍物进行时间段运动采样,得到了障碍物每隔0.1s的坐标位置,那么只要需要计算每个采样点和这些运动的坐标位置cost,求和就可以每个动态障碍物的cost。
// Simple version: calculate obstacle cost by distance
ComparableCost TrajectoryCost::GetCostBetweenObsBoxes(
const Box2d &ego_box, const Box2d &obstacle_box) const {
ComparableCost obstacle_cost;
const float distance = obstacle_box.DistanceTo(ego_box);
if (distance > config_.obstacle_ignore_distance()) {
return obstacle_cost;
}
obstacle_cost.safety_cost += // A. 计算碰撞cost
config_.obstacle_collision_cost() * // obstacle_collision_cost: 1e8
Sigmoid(config_.obstacle_collision_distance() - distance); // obstacle_collision_distance: 0.5
obstacle_cost.safety_cost += // B. 计算风险cost
20.0 * Sigmoid(config_.obstacle_risk_distance() - distance); // obstacle_risk_distance: 2.0
return obstacle_cost;
}
从代码可以得到如下结论:
结论1:动态障碍物计算需要考虑到每个时间点上障碍物的位置,每个时间点每个障碍物的cost计算分为碰撞cost和风险cost。
结论2:从计算公式可以看到,一样是Sigmoid,碰撞cost系数高达1e8,风险cost系数为20,所以Apollo对障碍物碰撞惩罚是非常高的,同样对存在风险的位置也有较高的惩罚。碰撞要求障碍物和无人车在约0.5m以内;风险则定义在2m以内。
Q4. 如何生成一条最小cost的路径?
当计算完每个node的最优路径(起始规划点到改点具有最小的cost),那么就可以计算从起始规划点到终点的最优路径。首先终点不止一个,也就是所有终点采样点的累计距离s是一致的,但是侧方相对距离l是在一个区间内的,所以:
step 1:选择最后一个level中,具有最小cost的node最为规划终点
bool DPRoadGraph::GenerateMinCostPath(
// find best path
DPRoadGraphNode fake_head;
for (const auto &cur_dp_node : graph_nodes.back()) { // 在最后一个level中查找
fake_head.UpdateCost(&cur_dp_node, cur_dp_node.min_cost_curve, cur_dp_node.min_cost);
}
}
step 2: 根据父指针向前遍历,得到至后向前的一条路径,倒置一下就是cost最小的路径
bool DPRoadGraph::GenerateMinCostPath(
const auto *min_cost_node = &fake_head;
while (min_cost_node->min_cost_prev_node) {
min_cost_node = min_cost_node->min_cost_prev_node;
min_cost_path->push_back(*min_cost_node);
}
if (min_cost_node != &graph_nodes.front().front()) {
return false;
}
std::reverse(min_cost_path->begin(), min_cost_path->end());
}
额外补充一点,如果和比较两个节点的cost,除了cost有对应的值,还有三个优先级状态:
- HAS_COLLISION: 存在碰撞
- OUT_OF_BOUNDARY:超出边界
- OUT_OF_LANE:超出车道
三个优先级依次从高到低。在比较两个cost(ComparableCost)时,首先比较cost优先级,如果优先级不一样,那么优先级高的cost大(不看cost值大小);如果优先级一样,才比较cost值大小。
路径决策器–PathDecider
这里的PathDecider与ReferenceLineInfo中的PathDecision很相似,PathDecision在Frame类初始化的过程中为每个PathObstacle添加标签,这个标签代表该障碍物的存在会对无人车造成什么影响。在初始化过程中,代码中仅仅利用路况以及路况中的障碍物位置,初步设定了障碍物的标签,例如人行横道路况下,在人行横道上的障碍物会无人车的影响,那么可以忽略,那么需要构建虚拟停车墙。但对于那些不在特殊路况下的障碍物(车辆虽然在道路线,但既不在停车区也不在禁停区交叉口等特殊区域),Frame初始化的工作就没有为这些障碍物分配标签。
通过路径规划器已经为无人车规划好了一条行驶路线,那么根据这条规划路线和障碍物属性(位置),就可以再一次更新障碍物的标签。例如有些障碍物在行驶路线上,那么就需要分这些障碍物分配停车Stop或者绕行SidePass等标签。
另外一个注意点,因为规划的路线只有位置信息,没有时间信息,所以路径决策器PathDecider仅仅只能为静态障碍物设定标签,无法为动态障碍物设定标签(动态障碍物需要在速度决策器SpeedDecider中更新标签)。
更新的过程其实比较简单,主要遵循一下原则:
- 非行人或者非机动车且非静态障碍物,忽略
- 前方和侧方已经存在忽略标签的障碍物,忽略
- 障碍物存在前方停车标签,忽略
- 障碍物存在侧方绕行标签,忽略
- 障碍物所在区域在禁停区,忽略
- 障碍物在规划路线以外,忽略
- 如果障碍物和无人车侧方距离大于一个阈值(半车距离+3m),那么障碍物侧方增加忽略标签
- 否则如果障碍物和无人车侧方距离小于一个阈值(半车距离+0.5m),那么就必须设置为停车
- 否者障碍物和无人车侧方距离在[半车距离+0.5m, 半车距离+3m]之间,允许左右微调,就将障碍物标签设置为微调
速度规划器(动态规划)–DpStSpeedOptimizer
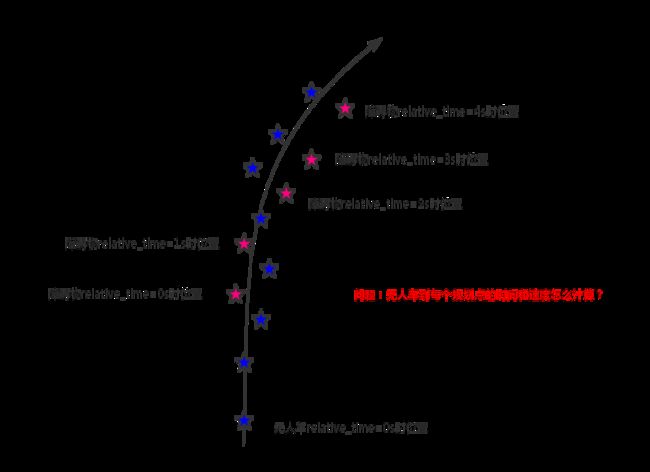
在路径规划中,已经给出了一条从规划起始点到规划终点开销cost最小的路径,如下图的蓝色星星组成的路径,每个蓝色的路径点都有相对于参考线的累计距离s和侧方相对距离l。那么剩下最后一个问题:每个规划点的速度怎么设定?换句话说无人车应该在什么时间点到达轨迹点?这就需要考虑障碍物在每个时间间隔的位置。
先看一下代码结构:
/// file in apollo/modules/planning/planner/em/em_planner.cc
Status EMPlanner::Plan(const TrajectoryPoint& planning_start_point, Frame* frame) {
for (auto& reference_line_info : frame->reference_line_info()) { // 先分别对每条参考线进行规划
auto cur_status = PlanOnReferenceLine(planning_start_point, frame, &reference_line_info); // 规划主函数
}
Status EMPlanner::PlanOnReferenceLine(
const TrajectoryPoint& planning_start_point, Frame* frame,
ReferenceLineInfo* reference_line_info) {
for (auto& optimizer : tasks_) { // 对每条参考线分别进行所有任务的规划,包括速度规划、路径位置规划、位置决策器规划等。
ret = optimizer->Execute(frame, reference_line_info);
}
}
/// file in apollo/modules/planning/tasks/speed_optimizer.cc
apollo::common::Status SpeedOptimizer::Execute(
Frame* frame, ReferenceLineInfo* reference_line_info) {
Task::Execute(frame, reference_line_info);
auto ret = Process( // 最终会调用速度规划类的Process函数
reference_line_info->AdcSlBoundary(), reference_line_info->path_data(),
frame->PlanningStartPoint(), reference_line_info->reference_line(),
*reference_line_info->mutable_speed_data(),
reference_line_info->path_decision(),
reference_line_info->mutable_speed_data());
return ret;
}
/// file in apollo/modules/planning/tasks/dp_st_speed/dp_st_speed_optimizer.cc
Status DpStSpeedOptimizer::Process(const SLBoundary& adc_sl_boundary,
const PathData& path_data,
const TrajectoryPoint& init_point,
const ReferenceLine& reference_line,
const SpeedData& reference_speed_data,
PathDecision* const path_decision,
SpeedData* const speed_data) {
path_decision->EraseStBoundaries();
if (boundary_mapper.CreateStBoundary(path_decision).code() == ErrorCode::PLANNING_ERROR) {}
SpeedLimitDecider speed_limit_decider(adc_sl_boundary, st_boundary_config_, *reference_line_, path_data);
if (!SearchStGraph(boundary_mapper, speed_limit_decider, path_data,
speed_data, path_decision, st_graph_debug)) {}
return Status::OK();
}
整体的速度规划分为两个部分:
-
限制条件计算。包括障碍物st边界框,也就是某时刻无人车能前进的位置上下界;此外还有每个位置的速度限制(道路限速,超车限速等因素)
-
速度规划
Part 1. 障碍物st边界框计算–StBoundaryMapper::CreateStBoundary函数
对于每个障碍物以及他的预测轨迹(5s内,每0.1s有一个预测轨迹点)。只需要遍历每个障碍物预测轨迹点,然后去查询路径规划得到的路径点,如果两两有重叠,就可以构造一个(累计距离s,相对时间t)的一个锚点。
for (int i = 0; i < trajectory.trajectory_point_size(); ++i) {
const auto& trajectory_point = trajectory.trajectory_point(i);
const Box2d obs_box = obstacle.GetBoundingBox(trajectory_point);
const double step_length = vehicle_param_.front_edge_to_center();
for (double path_s = 0.0; path_s < discretized_path.Length(); // 在规划的路径下采样,每半车一个采样点
path_s += step_length) {
const auto curr_adc_path_point = // 计算采样点的累计距离s
discretized_path.EvaluateUsingLinearApproximation(
path_s + discretized_path.StartPoint().s());
if (CheckOverlap(curr_adc_path_point, obs_box, // 确认障碍物和无人车在该时间点是够有重叠,如果没有重叠,就可以忽略该时间点的障碍物
st_boundary_config_.boundary_buffer())) {
// found overlap, start searching with higher resolution
const double backward_distance = -step_length; // 下界初始距离
const double forward_distance = vehicle_param_.length() + // 上节初始距离
vehicle_param_.width() +
obs_box.length() + obs_box.width();
bool find_low = false;
bool find_high = false;
double low_s = std::fmax(0.0, path_s + backward_distance);
double high_s = std::fmin(discretized_path.Length(), path_s + forward_distance);
// 采用步步紧靠的方法,构造更紧凑的上下界low_s和high_s
while (low_s < high_s) {
...
if (find_high && find_low) {
lower_points->emplace_back( // 加入下界信息,对应在参考线上的累计距离s,和相对时间t(障碍物轨迹相对时间)
low_s - st_boundary_config_.point_extension(),
trajectory_point_time);
upper_points->emplace_back(
high_s + st_boundary_config_.point_extension(),
trajectory_point_time);
}
break;
}
}
}
}
从上面代码我们可以很清晰的看到这个(累计距离s,相对时间t)标定框的计算,这个标定框可以解释为,无人车再该时间点,可以行驶到的坐标上下界。同时也会根据无人车状态跟随follow,减速yield,超车overtake等情况设定边界框类型。这个上下界的st边界框将存储在PathObstacle中,是每个时刻障碍物的所在的区域标定框,无人车不能与该标定框有冲突。
Status StBoundaryMapper::MapWithDecision(
PathObstacle* path_obstacle, const ObjectDecisionType& decision) const {
// 计算障碍物的边界框,当且仅当障碍物再某个时刻与无人车规划路径有重叠时,才被考虑。
std::vector lower_points;
std::vector upper_points;
if (!GetOverlapBoundaryPoints(path_data_.discretized_path().path_points(),
*(path_obstacle->obstacle()), &upper_points,
&lower_points)) {
return Status::OK();
}
// 转成StBoundary,并且打上标签与数据,存入PathObstacle中
auto boundary = StBoundary::GenerateStBoundary(lower_points, upper_points)
.ExpandByS(boundary_s_buffer)
.ExpandByT(boundary_t_buffer);
// get characteristic_length and boundary_type.
StBoundary::BoundaryType b_type = StBoundary::BoundaryType::UNKNOWN;
double characteristic_length = 0.0;
if (decision.has_follow()) {
characteristic_length = std::fabs(decision.follow().distance_s());
b_type = StBoundary::BoundaryType::FOLLOW;
} else if (decision.has_yield()) {
characteristic_length = std::fabs(decision.yield().distance_s());
boundary = StBoundary::GenerateStBoundary(lower_points, upper_points)
.ExpandByS(characteristic_length);
b_type = StBoundary::BoundaryType::YIELD;
} else if (decision.has_overtake()) {
characteristic_length = std::fabs(decision.overtake().distance_s());
b_type = StBoundary::BoundaryType::OVERTAKE;
} else {
}
boundary.SetBoundaryType(b_type);
boundary.SetId(path_obstacle->obstacle()->Id());
boundary.SetCharacteristicLength(characteristic_length);
path_obstacle->SetStBoundary(boundary);
return Status::OK();
}
最后可以遍历所有的PathPbstacle,获取所有的障碍物在不同时刻的st边界框以及边界框类型,该部分由DpStSpeedOptimizer::SearchStGraph中完成,所有的st边界框将存储在boundaries中。
Part2 无人车速度限制–SpeedLimitDecider::GetSpeedLimits函数完成
这个函数做的工作就相对来说比较明显,计算规划路径中每个点所在位置的速度限制,速度限制来源于4方面:
- 车道本身限制,例如速度不大于60km/h
// (1) speed limit from map
double speed_limit_on_reference_line = reference_line_.GetSpeedLimitFromS(frenet_point_s);
- 向心加速度限制
// -- 2.1: limit by centripetal force (acceleration)
const double centri_acc_speed_limit =
std::sqrt(GetCentricAccLimit(std::fabs(avg_kappa[i])) /
std::fmax(std::fabs(avg_kappa[i]), st_boundary_config_.minimal_kappa()));
根据向心加速度公式: $ a = v ^2 / R = v^2 · kappa , 可 以 很 轻 松 的 计 算 速 度 : ,可以很轻松的计算速度: ,可以很轻松的计算速度: v = \sqrt(a / kappa)$。现在关键是向心加速度a如何计算,代码中在GetCentricAccLimit函数中实现,其实实现方法非常简单,根据(v_high, h_v_acc)和(v_low, l_v_acc)两个坐标点构建一个一元一次方程: $ y = av + b $,其中y是向心加速度,v是速度,a和b分别是斜率与截距。
斜率计算:$ a = (h_v_acc - l_v_acc) / (v_high - v_low) = k1 $
截距计算:$ b = h_v_acc - v_high * k1 = k2 $
最后给定kappa(k),可以得到对应的速度v:
$ v^2 · k = acc = a·v + b , 整 理 得 到 : ,整理得到: ,整理得到: k·v^2 - av - b = 0 $
根绝一元二次多项式的通用求解公式: $ v = (a + \sqrt(a^2 + 4kb))/2k $
const double v = (k1 + std::sqrt(k1 * k1 + 4.0 * kappa * k2)) / (2.0 * kappa);
if (v > v_high) {
return h_v_acc;
} else if (v < v_low) {
return l_v_acc;
} else {
return v * k1 + k2;
}
代码还对最终的v做了一个区间的截取。限定在[h_v_acc, l_v_acc]中。
- 向心力限制
// -- 2.2: limit by centripetal jerk
double centri_jerk_speed_limit = std::numeric_limits::max();
if (i + 1 < discretized_path_points.size()) {
const double ds = discretized_path_points.at(i + 1).s() - discretized_path_points.at(i).s();
const double kEpsilon = 1e-9;
const double centri_jerk =
std::fabs(avg_kappa[i + 1] - avg_kappa[i]) / (ds + kEpsilon);
centri_jerk_speed_limit = std::fmax(
10.0, st_boundary_config_.centri_jerk_speed_coeff() / centri_jerk);
}
这部分暂时没看透,留待后续完善。
- 无人车微调限制
遍历所有障碍物的侧方向标签,如果存在以下两种情况就需要微调速度:
情况1:障碍物标签为向左微调ObjectNudge::LEFT_NUDGE,并且无人车确实被障碍物阻挡
bool is_close_on_left =
(nudge.type() == ObjectNudge::LEFT_NUDGE) &&
(frenet_point_l - vehicle_param_.right_edge_to_center() - kRange <
const_path_obstacle->PerceptionSLBoundary().end_l());
情况2:障碍物标签为向右微调ObjectNudge::RIGHT_NUDGE,并且无人车确实被障碍物阻挡
bool is_close_on_right =
(nudge.type() == ObjectNudge::RIGHT_NUDGE) &&
(const_path_obstacle->PerceptionSLBoundary().start_l() - kRange <
frenet_point_l + vehicle_param_.left_edge_to_center());
这两种情况下,需要对速度做限制,因为车道限速60km/s,向左或者向右微调的时候速度肯定不允许这么大,必须要乘以一个折扣因子。对于静态障碍物,折扣系数为static_obs_nudge_speed_ratio(0.6);对于动态障碍物,由于障碍物也是运动的,所以允许系数大一点dynamic_obs_nudge_speed_ratio为0.8。
最终无人车在该规划点处的速度限制就是以上个速度的最小值,
基于动态规划方法的速度规划–DpStGraph::Search完成
目前已经知道:
- 障碍物在每个时间点的st边界框(t时刻障碍物的lower_和upper_s,只要该时刻无人车的累积路径距离s不在这个区间内,说明无人车在这个点和障碍物位置是安全的)。
- 累积距离方向上的速度限制,即[start_S,end_s]区间内有限制速度v_limit。
接下来如何规划未来时间段的无人车速度,或者说哪个时间点无人车应该出现在哪里。DpStSpeedOptimizer速度规划器依旧使用的是动态规划方法。具体的做法与上述基于动态对话的路径规划器是很类似的:
无人车需要对未来T时间,未来S距离内的时间距离进行规划,最简单的做法就是构建一张表格,例如大小为TxS,行代表0-T时刻的索引;列代表0-S距离上的索引。其中每个点table[t][s]就可以表示为初始规划点init_point到(相对时刻t,累积距离s)p2点的最小开销cost以及最小开销对应的父节点。例如现在有两个节点可以连接到table[t][s],分别为table[t-1][s-1]和table[t-1][s-2],那么可以分别计算两个节点到当前节点的开销cost1和cost2:
- table[t-1][s-2]到table[t][s]的开销为:
cost1 = total_cost(t-1,s-2) + edge_cost(t,s,t-1,s-2)
- table[t-1][s-1]到table[t][s]的开销为:
cost2 = total_cost(t-1,s-1) + edge_cost(t,s,t-1,s-1)
如果cost1小于cost2,那么table[t][s]的总体最小开销total_cost(t,s)就为cost1,且父节点指针指向table[t-1][s-2]。
最后如何寻找一条最优的路径?
第一个问题肯定是要找到最优的规划结束点。在路径规划中,最优规划结束点由若干个,这些点的累计距离s是一致的,但是侧方偏移距离l不一致。那么在速度规划中也存在这个问题,我们对未来T时刻和累积距离S的路程进行规划,那么最终的规划结束点可以是:
- T秒结束以后规划结果,对应table[T][m],m从0到S。(对应table最下行,规划时间一致,规划路径长度不一致)
- S规划距离结束的规划结果,对应table[n][S],n从0到T。(对应table最右列,规划路径长度一致,规划时间不一致)
选择最下行和最右列最小cost,然后自下而上可以找到一条cost最小的路径。下面可以参考一下代码的结构,总共分三步:
- 初始化cost表,对应上面例子中的table
- 循环计算cost表中每个元素的大小,也就是初始规划点init_point到(相对时刻t,累积距离s)p2点的最小开销cost
- 依靠父指针,反向寻找最小cost对应的路径
/// file in apollo/modules/planning/tasks/dp_st_speed/dp_st_graph.cc
Status DpStGraph::Search(SpeedData* const speed_data) {
constexpr float kBounadryEpsilon = 1e-2;
// Step 1. 初始化cost表,对应上面例子中的table
if (!InitCostTable().ok()) {
...
}
// Step B. 循环计算cost表中每个元素的大小,也就是初始规划点init_point到(相对时刻t,累积距离s)p2点的最小开销cost
if (!CalculateTotalCost().ok()) {
...
}
// Step C. 依靠父指针,反向寻找最小cost对应的路径
if (!RetrieveSpeedProfile(speed_data).ok()) {
}
return Status::OK();
}
Q1. 如何初始化表?–InitCostTable
初始化cost表比较简单,行代表不同时刻t,列代表不同累计距离s。
uint32_t dim_s = dp_st_speed_config_.matrix_dimension_s(); // 150m
uint32_t dim_t = dp_st_speed_config_.matrix_dimension_t(); // 8s
cost_table_ = std::vector>(dim_t, std::vector(dim_s, StGraphPoint()));
所以可以看到,cost表中对未来8s内以及前向150m的路程做了速度规划。且两行之间的时间差unit_t为1s;两列之间的距离距离差unit_s为1m。
Q2. 如何计算节点最小cost?-CalculateTotalCost-
计算表格的最小cost和每个表格节点的最小cost由函数DpStGraph::CalculateTotalCost和DpStGraph::CalculateCostAt完成。计算过程相对来说比较简单,一个节点table[t-1][s-1]连接当前节点table[t][s],那么当前节点的cost计算可以分为4部分:
- 障碍物项开销(节点内)
- 限速项开销cost(节点间EdgeCost)
- 加速度项开销cost(节点间EdgeCost)
- 加速度抖动开销cost(节点间EdgeCost)
节点内和节点间区别在于,节点内Cost也就是障碍物项惩罚只用到了当前时刻(t,s)的信息。而计算速度,加速度,加速度抖动需要用到前几个节点的信息,所以是节点间的cost,这么安排主要增加代码可读性。
- 当前节点(相对时间t,累积距离s)和障碍物运动轨迹的开销。
每个障碍物在未来的时间间隔内(例如5s,每0.1s就有一个采样的位置s)都有它的运动轨迹,也就是运动位置s_x。那么在相对时间t和累积距离s时刻,无人车会不会和障碍物该时刻相撞呢?这部分就需要计算无人车和障碍物在t时刻的位置信息,也就是位置cost。
void DpStGraph::CalculateCostAt(const uint32_t c, const uint32_t r) {
auto& cost_cr = cost_table_[c][r];
cost_cr.SetObstacleCost(dp_st_cost_.GetObstacleCost(cost_cr));
}
障碍物位置开销思路比较简单,循环每个障碍物,计算t时刻障碍物st边界框的上界和下届,只需要无人车的位置(t,s)与边界框不重合即可。
首先肯定要判断
- 是不是障碍物的标签是禁停?是的话就不需要有cost,对无人车限制不了。cost=0
- t时刻障碍物轨迹是否存在(障碍物轨迹时间为min_t-max_t)?不存在,cost=0
- t时刻无人车是否和障碍物冲突了?是的话,cost无穷大。
否则计算障碍物在t时刻的上界和下界位置,即上下界的累积距离s。为了避免其他节点再一次计算(t,s)时刻的障碍物上下界,可以采用缓存技术,只需要计算一次即可。
// 利用缓存加速计算。GetBoundarySRange函数可以用来计算t时刻障碍物上界和下界累积距离s,并缓存
if (boundary_cost_[boundary_index][st_graph_point.index_t()].first < 0.0) {
boundary.GetBoundarySRange(t, &s_upper, &s_lower);
boundary_cost_[boundary_index][st_graph_point.index_t()] = std::make_pair(s_upper, s_lower);
} else {
s_upper = boundary_cost_[boundary_index][st_graph_point.index_t()].first;
s_lower = boundary_cost_[boundary_index][st_graph_point.index_t()].second;
}
如果t时刻无人车在障碍物后方,cost计算方法为:
if (s < s_lower) {
constexpr float kSafeTimeBuffer = 3.0;
const float len = obstacle->obstacle()->Speed() * kSafeTimeBuffer; // 计算安全距离
if (s + len < s_lower) { // 如果障碍物和无人车在t时刻距离大于安全距离,距离比较远,cost=0
continue;
} else { // 否则距离小于安全距离,计算cost。obstacle_weight:1.0,default_obstacle_cost:1000,
cost += config_.obstacle_weight() * config_.default_obstacle_cost() *
std::pow((len - s_lower + s), 2);
}
}
如果t时刻无人车在障碍物前方,cost计算方法为:
else if (s > s_upper) {
const float kSafeDistance = 20.0; // 安全距离20米,也可以跟上面一样,根据速度来计算安全距离
if (s > s_upper + kSafeDistance) { // 如果障碍物和无人车在t时刻距离大于安全距离,距离比较远,cost=0
continue;
} else { // 否则距离小于安全距离,计算cost。obstacle_weight:1.0,default_obstacle_cost:1000,
cost += config_.obstacle_weight() * config_.default_obstacle_cost() *
std::pow((kSafeDistance + s_upper - s), 2);
}
}
最终(相对时间t,累积距离s)所在的节点的障碍物开销就是所有障碍物个体开销的总和,每个个体开销计算方法如上。经过分析可以看到,个体障碍物开销大小取决于t时刻障碍物和无人车的距离,并与距离差平方成正比。
- 速度限制开销
通过两个节点的累计距离s,和节点间的时间差unit_t,可以间接计算时间段[t-1,t]内的平均速度。
- 如果速度小于最大速度,并且在禁停区内,计算方式为:
if (speed < FLAGS_max_stop_speed && InKeepClearRange(second.s())) {
// first.s in range
cost += config_.keep_clear_low_speed_penalty() * unit_t_ * // keep_clear_low_speed_penalty:10
config_.default_speed_cost(); // default_speed_cost: 10
}
- 计算当前速度和限速的差值比,小于0说明比限制速度小。
float det_speed = (speed - speed_limit) / speed_limit;
if (det_speed > 0) { // exceed_speed_penalty: 10, default_speed_cost: 10
cost += config_.exceed_speed_penalty() * config_.default_speed_cost() *
fabs(speed * speed) * unit_t_;
} else if (det_speed < 0) { // low_speed_penalty: 10, default_speed_cost: 10
cost += config_.low_speed_penalty() * config_.default_speed_cost() *
-det_speed * unit_t_;
}
所以从上面计算方法可以得到以下结论:
结论1:在禁停区需要有一定的cost。
结论2:代码鼓励无人车在该路径段内行驶速度低于最高限速,可以看到该情况下cost小于0,有奖励。反之超速了,惩罚与速度平法成正比。
- 加速度开销
GetAccelCostByThreePoints函数和GetAccelCostByTwoPoints函数本质是一样的,区别在于计算t时刻的加速度,前者利用3个节点的累积距离s1,s2,s3来计算,计算公式为:
accel = (first.s() + third.s() - 2 * second.s()) / (unit_t_ * unit_t_)
后者使用两个节点和初始速度来计算加速度:
float current_speed = (curr_point.s() - pre_point.s()) / unit_t_;
float accel = (current_speed - pre_speed) / unit_t_;
无论是哪种方法,最后都套用公式: a = (v2 - v1) / t
const float accel_sq = accel * accel;
float max_acc = config_.max_acceleration(); // 3.0 m/s^2
float max_dec = config_.max_deceleration(); // -4.0 m/s^2
float accel_penalty = config_.accel_penalty(); // 1.0
float decel_penalty = config_.decel_penalty(); // 1.0
if (accel > 0.0) { // 计算加速度正情况下cost
cost = accel_penalty * accel_sq;
} else { // 计算加速度负情况下cost
cost = decel_penalty * accel_sq;
}
cost += accel_sq * decel_penalty * decel_penalty / // 总体cost
(1 + std::exp(1.0 * (accel - max_dec))) +
accel_sq * accel_penalty * accel_penalty /
(1 + std::exp(-1.0 * (accel - max_acc)));
accel_cost_.at(accel_key) = cost;
为了加速计算,这里也是用了缓存技术,避免重复计算的问题。这里的结论也比较简单,为了统一加速度正负情况,这里使用了sigmod函数来获得一致性。
- 加速度抖动开销
就速度抖动,其实也就是加速度的导数。
const float jerk = (curr_acc - pre_acc) / unit_t_;
抖动开销计算方法为:
float jerk_sq = jerk * jerk;
if (jerk > 0) {
cost = config_.positive_jerk_coeff() * jerk_sq * unit_t_; // positive_jerk_coeff: 1.0
} else {
cost = config_.negative_jerk_coeff() * jerk_sq * unit_t_; // negative_jerk_coeff: 1.0
}
jerk_cost_.at(jerk_key) = cost;
最后额外注意几个细节:
细节1:DpStGraph::CalculateCostAt中使用的
if (cost < cost_cr.total_cost()) {
cost_cr.SetTotalCost(cost);
cost_cr.SetPrePoint(pre_col[r_pre]);
}
这里其实是对当前节点(t,s)选择一个具有最小cost的父节点。每次循环都进行一次cost比较,保证最后cost_cr具有最小的惩罚,以及最小惩罚对应的父节点。
细节2:DpStGraph::CalculateTotalCost函数中next_highest_row和next_lowest_row的运用
for (uint32_t r = next_lowest_row; r <= next_highest_row; ++r) {
const auto& cost_cr = cost_table_[c][r];
if (cost_cr.total_cost() < std::numeric_limits::infinity()) {
int h_r = 0;
int l_r = 0;
GetRowRange(cost_cr, &h_r, &l_r);
highest_row = std::max(highest_row, h_r);
lowest_row = std::min(lowest_row, l_r);
}
}
next_highest_row = highest_row;
next_lowest_row = lowest_row;
这部分计算的next_highest_row和next_lowest_row作用就是为了减少计算量。例如当前节点是(t,s),那么根据当前最大规划速度v就可以计算unit_t时刻以后,无人车的累积距离最大为s+3,那么就可以简单地将下一层计算限制在[t+1,s]到[t+1,s+3]内。而不用计算t+1行所有节点和当前节点的连接,因为部分节点和当前节点过远,在unit_t以后根本到不了,所以不需要计算。
Q3:如何找一条cost最小的速度规划轨迹?–RetrieveSpeedProfile
Step 1. 寻找最后一行(t=T)和最右一列(s=S)中最小的cost对应的节点,作为规划终点
const StGraphPoint* best_end_point = nullptr;
for (const StGraphPoint& cur_point : cost_table_.back()) {
if (!std::isinf(cur_point.total_cost()) &&
cur_point.total_cost() < min_cost) {
best_end_point = &cur_point;
min_cost = cur_point.total_cost();
}
}
for (const auto& row : cost_table_) {
const StGraphPoint& cur_point = row.back();
if (!std::isinf(cur_point.total_cost()) &&
cur_point.total_cost() < min_cost) {
best_end_point = &cur_point;
min_cost = cur_point.total_cost();
}
}
Step 2. 从最小cost的节点自下而上直至规划起始点,找到最小cost的规划路径
std::vector speed_profile;
const StGraphPoint* cur_point = best_end_point;
while (cur_point != nullptr) {
SpeedPoint speed_point;
speed_point.set_s(cur_point->point().s());
speed_point.set_t(cur_point->point().t());
speed_profile.emplace_back(speed_point);
cur_point = cur_point->pre_point();
}
std::reverse(speed_profile.begin(), speed_profile.end());
速度决策器–SpeedDecider
与路径决策器思路一致,当路径规划器完成路径规划以后,可以得到一条无人车的最优行驶路线,路径决策器就需要对静态障碍物做标签的更新,尤其是那些不在特殊路况下的障碍物,由于缺乏时间信息,路径决策器PathDecider无法对动态障碍物进行标签更新。
而在速度规划器完成未来时间8s或者未来前向距离150m的规划以后,已经得到了一条未来每个时刻无人车出现在参考线上的位置(累积距离s),再配合事先已经规划好的路径,就可以完成对动态障碍物的标签更新,这里仅仅对最近的st障碍物边界框做标签更新,没有对所有的预测时间进行更新。
更新规则如下:
- 对于每个障碍物进行更新,如果障碍物已经在无人车后,那么添加忽略
if (boundary.IsEmpty() || boundary.max_s() < 0.0 ||
boundary.max_t() < 0.0 ||
boundary.min_t() > dp_st_speed_config_.total_time()) {
AppendIgnoreDecision(path_obstacle); // 如果前方或者侧方已存在标签,那么跳过,否则加上ignore的标签
continue;
}
- 计算最近障碍物st边界框对应速度规划上的上下界速度点(组成一条速度线):
- 如果无人车在障碍物的后方BELOW:
- 如果st框的类型为禁停,那么设置为停车(个人理解为先停车前方障碍物驶过,再进入禁停区,因为禁停区无法停车。是否设置跟车也可以?)
- 否则如果障碍物速度大,可以设置为跟车,障碍物速度小可以设置为停车
- 如果无人车在障碍物的前方ABOVE:
- 如果st框的类型为禁停,那么可以忽略(因为已经过了禁停区)
- 否则就设置为超车(已经超过了)
- 如果无人车和障碍物路径有重叠CROSS,如果被锁(也就是非禁停区障碍物),那么就必须停车等待。
- 其余情况障碍物标签设置为忽略
速度规划器(二次规划)–QpSplineStSpeedOptimizer
其实上面已经给了基于动态规划解决方案的速度规划器,思路也比较简单,虽然能预测到每个相对时间点t无人车的位置s,但是动态规划版本的速度规划器对无人车的速度v、加速度a以及方向theta等信息处理能力较弱,只能通过临近几个st节点来估测,存在偏差。而基于二次规划QP的速度规划器,实用多项式拟合st点,得到多项式函数,这时候就可以根据导数求速度,二阶导求加速度等信息。也可以参考官方文档
在指引线提供器: ReferenceLineProvider中,我们已经给出了基于二次规划QP的参考线平滑技术,这里的速度规划其实与参考线平滑很类似,主要的步骤分为:
1. 预处理
参考线平滑中的预处理工作是采样,也就是决定设置多少节点knots,每两个knots节点中间采集多少个拟合点;在QP速度规划器中,预处理工作就和DP规划器一样,生成障碍物所有预测时刻的st边界框,设置不同区域的限速。
速度规划器中设置了4段,共8s时间,所以应该是5个knots,分别对应0,2,4,6,8s。但是代码中有个疑惑,存储了4个knots(t_knots_.size(): 4),后面计算段函数的时候依旧使用t_knots_.size(),导致了少1,所以是够在这里有存在问题?因此每段同样使用一个5次多项式去拟合。可以得到一下信息:
- 4段共4个5次多项式拟合函数,每个函数定义域为[0,2]。(spline_order_: 5)
- 拟合多项式共包含参数: 4 * (5+1)
void QpSplineStGraph::Init() {
double curr_t = 0.0;
uint32_t num_spline = // num_spline = 3
qp_st_speed_config_.qp_spline_config().number_of_discrete_graph_t() - 1;
for (uint32_t i = 0; i <= num_spline; ++i) {
t_knots_.push_back(curr_t);
curr_t += t_knots_resolution_; // t_knots_resolution_: 2s
}
uint32_t num_evaluated_t = 10 * num_spline + 1;
// init evaluated t positions
curr_t = 0;
t_evaluated_resolution_ =
qp_st_speed_config_.total_time() / (num_evaluated_t - 1);
for (uint32_t i = 0; i < num_evaluated_t; ++i) {
t_evaluated_.push_back(curr_t);
curr_t += t_evaluated_resolution_;
}
}
这段代码有疑惑,下面knots生成的过程中,t_knots_的数量比num_spline多1,那么明显num_spline代表了拟合过程中使用多少段函数,为什么需要减去1?而且t_knots_的存储记录为[0,2,4,6],所以只能规划未来6s内的(t,s)。但在后续采样t_evaluated_的时候又使用了total_time 8s来计算。所以这里有点困惑,是不是应该num_spline就等于number_of_discrete_graph_t呢?
2. 约束条件设置
由于已经在参考线平滑中非常详细的讲解QP约束条件(包括等式约束和不等式约束),这里就相对简单地讲解约束类型,对具体的数学形式不做讨论,如果想具体了解,可以参考指引线提供器: ReferenceLineProvider,速度规划器中的求解和参考线平滑中的QP问题求解方法是高度一致的,
- 等式约束1:多项式函数必须经过原点,也就是t=0,delta_s=0(无人车当前位置)
注意:这里的s是所有物体的位置(累积距离s)相对于无人车当前位置的偏移距离,这和参考线拼接中,第一个anchor_point(knots)为原点,其他点的坐标x和y都是相对于该点的偏移坐标。
if (!constraint->AddPointConstraint(0.0, 0.0)) {
...
}
- 等式约束2:原点处的斜率,必须等于规划起始点速度
if (!constraint->AddPointDerivativeConstraint(0.0, init_point_.v())) {
...
}
- 不等式约束3:函数单调性约束
拟合函数x轴是相对时间t,y轴是无人车规划位置相对于规划起始点的偏移距离delta_s。所以随着相对时间的增加,delta_s总是单调递增(无人车时刻在前进)。如何设置这个约束,代码中就对[0,8]秒这个区间进行均匀采样,大致采样31个点。
uint32_t num_evaluated_t = 10 * num_spline + 1; // 10 * 3 +1
// init evaluated t positions
curr_t = 0;
t_evaluated_resolution_ = qp_st_speed_config_.total_time() / (num_evaluated_t - 1); // 8/30
for (uint32_t i = 0; i < num_evaluated_t; ++i) {
t_evaluated_.push_back(curr_t);
curr_t += t_evaluated_resolution_;
}
只要满足num_evaluated_t中每个点对应的y值,单调递增即可,换句话说只要保证后一个点减去前一个点的函数值大于零。
uint32_t prev_spline_index = FindIndex(x_coord[0]);
double prev_rel_x = x_coord[0] - x_knots_[prev_spline_index];
std::vector prev_coef;
GeneratePowerX(prev_rel_x, num_params, &prev_coef); // 前一个点的多项式系数[1, x0, x0^2, x0^3, x0^4, x0^5]
for (uint32_t i = 1; i < x_coord.size(); ++i) {
uint32_t cur_spline_index = FindIndex(x_coord[i]); // 寻找当前点所在段
double cur_rel_x = x_coord[i] - x_knots_[cur_spline_index]; // 相对时间减去所在段的首knots时间,就可以得到自变量的范围[0,2]
std::vector cur_coef;
GeneratePowerX(cur_rel_x, num_params, &cur_coef); // 后一个点的多项式系数[1, x1, x1^2, x1^3, x1^4, x1^5]
// if constraint on the same spline
if (cur_spline_index == prev_spline_index) { // 同一个段函数内,直接相减即可,使用同一阻系数[ai_0, ai_1, ai_2, ai_3, ai_4, ai_5]
for (uint32_t j = 0; j < cur_coef.size(); ++j) {
inequality_constraint(i - 1, cur_spline_index * num_params + j) =
cur_coef[j] - prev_coef[j];
}
} else { // 不同段函数,需要错开位置,因为使用的系数不一样
// if not on the same spline
for (uint32_t j = 0; j < cur_coef.size(); ++j) {
inequality_constraint(i - 1, prev_spline_index * num_params + j) =
-prev_coef[j];
inequality_constraint(i - 1, cur_spline_index * num_params + j) =
cur_coef[j];
}
}
prev_coef = cur_coef;
prev_spline_index = cur_spline_index;
}
- 等式约束4:段拟合函数间平滑约束
现共有4段拟合函数,和参考线平滑中完全相同。相邻两个段拟合函数之间,必须保证:
- 前一个函数终点和后一个函数起点函数值相同,即连续对应相对时间t时刻,两段上无人车的位置必须是相同的
- 前一个函数终点和后一个函数一阶导相同,对应相对时间t时刻,两段上无人车的速度必须是相同的
- 前一个函数终点和后一个函数二阶导相同,对应相对时间t时刻,两段上无人车的加速度必须是相同的
- 前一个函数终点和后一个函数三阶导相同,对应相对时间t时刻,两段上无人车的加速度抖动必须是相同的
所以总结一下,这部分等式约束数量,共5个knots_(4个段函数),两两之间需要3次平滑,每次平滑需要上述4个公式,所以这部分最后的等式约束数量为:(t_knots_.size()-2)*4
bool Spline1dConstraint::AddThirdDerivativeSmoothConstraint() {
const uint32_t n_constraint = (x_knots_.size() - 2) * 4; // 约束不等式数量
const uint32_t num_params = spline_order_ + 1; // 5+1=6
Eigen::MatrixXd equality_constraint =
Eigen::MatrixXd::Zero(n_constraint, (x_knots_.size() - 1) * num_params);
Eigen::MatrixXd equality_boundary = Eigen::MatrixXd::Zero(n_constraint, 1);
- 不等式约束5:边界框约束
实现已经采样了t_evaluated_,从[0,8]秒区间内均匀采样了31个点,每两个点之间的距离为8/30。所以边界约束,只要计算所有障碍物在每个采样点内的st边界框,满足规划点也就是delta_s=f(t)在st边界框外面即可。
- 不等式约束6:限速约束
这个过程也比较简单,只要计算t_evaluated_中每个点对应的上下界,下届为0,上界为距离该点最近一个限速区的限速。最后同5一样,每个点的速度,也就是函数一阶导约束在上下界之间。
- 不等式约束7:加速度约束
加速度约束和速度约束,边界框约束一样,但是加速度约束更简单,直接在配置文件中给出了。
preferred_max_acceleration: 2.5
preferred_min_deceleration: -3.3
max_acceleration: 3.0
min_deceleration: -4.5
先使用第一组(preferred_max_acceleration && preferred_min_deceleration)去求解QP,如果不成功换第二组(max_acceleration && min_deceleration)。相比第一组,第二组的区间更大,约束能力稍小,优化成功的可能性更高。
3. 核设置,也就是QP形式中优化目标和正则惩罚项设置
按照Apollo文档,cost函数主要分为三部分,第一部分就是f(t)的积分运算,这和参考线平滑也是一致,只是参考线平滑中只用到三阶导数,而这里用了二阶和三阶导,求解方法和后者一样:
c o s t 1 = ∑ i = 1 n ( w 1 ⋅ ∫ 0 d i ( f i ′ ) 2 ( s ) d s + w 2 ⋅ ∫ 0 d i ( f i ′ ′ ) 2 ( s ) d s + w 3 ⋅ ∫ 0 d i ( f i ′ ′ ′ ) 2 ( s ) d s ) cost_1 = \sum_{i=1}^{n} \Big( w_1 \cdot \int\limits_{0}^{d_i} (f_i')^2(s) ds + w_2 \cdot \int\limits_{0}^{d_i} (f_i'')^2(s) ds + w_3 \cdot \int\limits_{0}^{d_i} (f_i^{\prime\prime\prime})^2(s) ds \Big) cost1=i=1∑n(w1⋅0∫di(fi′)2(s)ds+w2⋅0∫di(fi′′)2(s)ds+w3⋅0∫di(fi′′′)2(s)ds)
if (qp_st_speed_config_.qp_spline_config().accel_kernel_weight() > 0) {
spline_kernel->AddSecondOrderDerivativeMatrix( // 对应上述第二项,二阶导平方的积分
qp_st_speed_config_.qp_spline_config().accel_kernel_weight());
}
if (qp_st_speed_config_.qp_spline_config().jerk_kernel_weight() > 0) {
spline_kernel->AddThirdOrderDerivativeMatrix( // 对应上述第三项,三阶导平方的积分
qp_st_speed_config_.qp_spline_config().jerk_kernel_weight());
}
第二部分是需要保证拟合的st路径和最终的st路径相似
c o s t 2 = ∑ i = 1 n ∑ j = 1 m ( f i ( t j ) − s j ) 2 cost_2 = \sum_{i=1}^{n}\sum_{j=1}^{m}\Big(f_i(t_j)- s_j\Big)^2 cost2=i=1∑nj=1∑m(fi(tj)−sj)2
Status QpSplineStGraph::AddCruiseReferenceLineKernel(const double weight) {
auto* spline_kernel = spline_generator_->mutable_spline_kernel();
double dist_ref = qp_st_speed_config_.total_path_length();
for (uint32_t i = 0; i < t_evaluated_.size(); ++i) {
cruise_.push_back(dist_ref);
}
if (t_evaluated_.size() > 0) {
spline_kernel->AddReferenceLineKernelMatrix(
t_evaluated_, cruise_, // weight: 0.3
weight * qp_st_speed_config_.total_time() / t_evaluated_.size());
}
}
bool Spline1dKernel::AddReferenceLineKernelMatrix(
const std::vector& x_coord, const std::vector& ref_x,
const double weight) {
const uint32_t num_params = spline_order_ + 1;
for (uint32_t i = 0; i < x_coord.size(); ++i) {
double cur_index = FindIndex(x_coord[i]);
double cur_rel_x = x_coord[i] - x_knots_[cur_index];
// update offset
double offset_coef = -2.0 * ref_x[i] * weight;
for (uint32_t j = 0; j < num_params; ++j) { // b = [1, t, t^2, t^3, t^4, t^5] * weight
offset_(j + cur_index * num_params, 0) += offset_coef;
offset_coef *= cur_rel_x;
}
// update kernel matrix
Eigen::MatrixXd ref_kernel(num_params, num_params);
for (uint32_t r = 0; r < num_params; ++r) {
for (uint32_t c = 0; c < num_params; ++c) {
ref_kernel(r, c) = 2.0 * power_x[r + c]; // T^TT = ref_kernel = [1, t, t^2, t^3, t^4, t^5]^t · [1, t, t^2, t^3, t^4, t^5]
}
}
kernel_matrix_.block(cur_index * num_params, cur_index * num_params,
num_params, num_params) += weight * ref_kernel;
}
return true;
}
代码中给出的方案是:$ 2x^THx + x^Tg(w0) $
$ x^THx 本 质 上 是 本质上是 本质上是 ATTTTA , T 是 ,T是 ,T是 [1, t, t^2, t^3, t^4, t5]T $,A对应系数向量。其中2H对应的ref_kernel,也就是系数矩阵,g(w0)是对应offset_coef。权值weight = 0.3*8/31.
第三部分是跟车情况下cost,这部分就要求跟车的时候,距离一定要保持在一定范围内,不能被甩的太开,也就是跟进前车,保持效率:
Status QpSplineStGraph::AddFollowReferenceLineKernel(
const std::vector& boundaries, const double weight) {
auto* spline_kernel = spline_generator_->mutable_spline_kernel();
std::vector ref_s;
std::vector filtered_evaluate_t;
for (size_t i = 0; i < t_evaluated_.size(); ++i) {
const double curr_t = t_evaluated_[i];
double s_min = std::numeric_limits::infinity();
bool success = false;
for (const auto* boundary : boundaries) { // 如果st边界框不是跟车,则忽略
if (boundary->boundary_type() != StBoundary::BoundaryType::FOLLOW) {
continue;
}
if (curr_t < boundary->min_t() || curr_t > boundary->max_t()) {
continue;
}
double s_upper = 0.0;
double s_lower = 0.0;
if (boundary->GetUnblockSRange(curr_t, &s_upper, &s_lower)) {
success = true;
s_min = std::min( // 强调跟车需要在follow_drag_distance,即17m内,不能太慢影响效率。
s_min,
s_upper - boundary->characteristic_length() -
qp_st_speed_config_.qp_spline_config().follow_drag_distance());
}
}
if (success && s_min < cruise_[i]) {
filtered_evaluate_t.push_back(curr_t);
ref_s.push_back(s_min);
}
}
if (!ref_s.empty()) {
spline_kernel->AddReferenceLineKernelMatrix(
filtered_evaluate_t, ref_s,
weight * qp_st_speed_config_.total_time() / t_evaluated_.size());
}
}
代码中给出的方案是:$ 2x^THx + x^Tg(w0) $。但是此时的b权值为weight=5.0*8/31
第四部分是减速cost,与二三部分形式一致,只有weight不一样,这里weight=100*8/31。此外加速需要要求无人车和障碍物距离不超过20m。
第五部分就是综合DP速度规划器和QP速度规划的结果,需要保证两者相差不能太多:
bool QpSplineStGraph::AddDpStReferenceKernel(const double weight) const {
std::vector t_pos;
std::vector s_pos;
for (auto point : reference_dp_speed_points_) { // DP速度规划器结果
t_pos.push_back(point.t());
s_pos.push_back(point.s());
}
auto* spline_kernel = spline_generator_->mutable_spline_kernel();
if (!t_pos.empty()) {
spline_kernel->AddReferenceLineKernelMatrix(
t_pos, s_pos, weight * qp_st_speed_config_.total_time() / t_pos.size());
}
return true;
}
在这里权重为0.0,所以说其实这里没有比较DP和QP速度规划器的结果。
最后一部分是正则化惩罚项alpha*A^TA,alpha系数为0.1。
4. 使用第三方库(qpOASES)求解二次规划问题
请参考开源软件qpOASES
最后其实可以看到QP速度规划器结果会覆盖DQ的结果,所以这里还是变相的使用了QP速度规划器来做速度规划。
// extract output
speed_data->Clear(); // 清除DP规划器结果
const Spline1d& spline = spline_generator_->spline();
const double t_output_resolution = FLAGS_trajectory_time_min_interval;
double time = 0.0;
while (time < qp_st_speed_config_.total_time() + t_output_resolution) {
double s = spline(time);
double v = std::max(0.0, spline.Derivative(time));
double a = spline.SecondOrderDerivative(time);
double da = spline.ThirdOrderDerivative(time);
speed_data->AppendSpeedPoint(s, time, v, a, da);
time += t_output_resolution;
}
速度规划结果与路径规划结果融合
路径规划得到关于(相对累积距离s,相对侧方距离l)的路径;速度规划得到关于(相对时间t,相对累计距离s)的路径。如何生成一条完整的(相对时间t,相对累积距离s,相对侧方距离l)的最优规划路径(该ReferenceLine参考线最优规划路径),而非全局最优。只需要对于每个速度点(具有相对时间、相对累计距离,但是缺乏侧方相对距离),只需要取他的相对累计距离s,去查询规划路径中的投影点得到该距离上的侧方累积距离l即可。
/// file in apollo/modules/planning/common/reference_line_info.cc
bool ReferenceLineInfo::CombinePathAndSpeedProfile(
const double relative_time, const double start_s,
DiscretizedTrajectory* ptr_discretized_trajectory) {
CHECK(ptr_discretized_trajectory != nullptr);
for (double cur_rel_time = 0.0; cur_rel_time < speed_data_.TotalTime(); // 对于每个速度点
cur_rel_time += (cur_rel_time < kDenseTimeSec ? kDenseTimeResoltuion
: kSparseTimeResolution)) {
common::SpeedPoint speed_point;
if (!speed_data_.EvaluateByTime(cur_rel_time, &speed_point)) {
AERROR << "Fail to get speed point with relative time " << cur_rel_time;
return false;
}
if (speed_point.s() > path_data_.discretized_path().Length()) {
break;
}
common::PathPoint path_point; // 使用速度点的相对累计距离去查询规划路径,得到对应的映射点
if (!path_data_.GetPathPointWithPathS(speed_point.s(), &path_point)) {
AERROR << "Fail to get path data with s " << speed_point.s()
<< "path total length " << path_data_.discretized_path().Length();
return false;
}
path_point.set_s(path_point.s() + start_s); // 加上起始点距离,变成"绝对"累积距离(实际上还是相对于参考线起始点的距离)
common::TrajectoryPoint trajectory_point; // 最后结合三者,可以生成一个新的完整路径点
trajectory_point.mutable_path_point()->CopyFrom(path_point);
trajectory_point.set_v(speed_point.v());
trajectory_point.set_a(speed_point.a());
trajectory_point.set_relative_time(speed_point.t() + relative_time);
ptr_discretized_trajectory->AppendTrajectoryPoint(trajectory_point);
}
return true;
}
此外再结合两者以后,还需要做一些判断,如果该参考线的最优规划路径过程中,有障碍物停车标签的,需要做一些惩罚,鼓励无人车在参考线前进过程中不要停车,以提升效率。
如果路径规划器或者速度规划器没有找到路径,需要为参考线增加一个cost(20000),障碍物迫使无人车停车,停车一次增加1000
Status EMPlanner::PlanOnReferenceLine(
const TrajectoryPoint& planning_start_point, Frame* frame,
ReferenceLineInfo* reference_line_info) {
if (reference_line_info->path_data().Empty()) {
GenerateFallbackPathProfile(reference_line_info,
reference_line_info->mutable_path_data());
reference_line_info->AddCost(kPathOptimizationFallbackClost); // 没有找到路径+20000
}
if (!ret.ok() || reference_line_info->speed_data().Empty()) {
ADEBUG << "Speed fallback.";
GenerateFallbackSpeedProfile(reference_line_info,
reference_line_info->mutable_speed_data());
reference_line_info->AddCost(kSpeedOptimizationFallbackClost); // 没有找到路径+20000
}
...
for (const auto* path_obstacle :
reference_line_info->path_decision()->path_obstacles().Items()) {
if (path_obstacle->obstacle()->IsVirtual()) {
continue;
}
if (!path_obstacle->obstacle()->IsStatic()) {
continue;
}
if (path_obstacle->LongitudinalDecision().has_stop()) {
constexpr double kRefrenceLineStaticObsCost = 1e3;
reference_line_info->AddCost(kRefrenceLineStaticObsCost); // 停车一次+1000
}
}
}
寻找全局最优路径
通过以上的路径规划,速度规划以及路径融合,每条参考线都可以得到其对应的最优规划路径以及具有cost。注意这个cost和路径规划中使用的cost不一样,路径规划中的cost仅仅是用来寻找最优路径,而参考线的cost是上面提到的三种,也是宏观意义上的cost。
/// file in apollo/modules/planning/common/frame.cc
const ReferenceLineInfo *Frame::FindDriveReferenceLineInfo() {
double min_cost = std::numeric_limits::infinity();
drive_reference_line_info_ = nullptr;
for (const auto &reference_line_info : reference_line_info_) {
if (reference_line_info.IsDrivable() &&
reference_line_info.Cost() < min_cost) {
drive_reference_line_info_ = &reference_line_info;
min_cost = reference_line_info.Cost();
}
}
return drive_reference_line_info_;
}
全局最优的路径相对来说比较简单,只需要寻找cost最小的参考线。
如有侵权,请联系本人删除!
参考资料:https://github.com/YannZyl/Apollo-Note/blob/master/docs/planning/em_planner.md