[统计]_怎样用数据炒菜：统计建模的两种文化

        这是之前发在个人公众号上的文章，希望能对读者有帮助。

        现在我们经常能听到一个概念叫做“大数据”，顾名思义，那就是海量的数据，如果再说大一点，那就是天量的数据，但是光有数据也不行，我们还希望这些数据能帮我们解决问题，从数据中得到我们问题的结论，这时候就需要借助我们的统计模型。如果把数据看作原材料的话，那统计建模就是拿数据炒菜的过程。

        那么我们怎么拿数据去炒菜呢？对于这个问题，20年前Leo Breiman教授有一个经典的回答，他的答案写在了《Statistical Modeling: The Two Cultures》（统计建模：两种文化）这篇文章里，这是一篇对统计学产生了深远影响的论文，这篇论文发表在2001年，到今天回顾这篇文章，都不得不佩服Breiman教授当时深刻的见解。

        统计学是一个比较有意思的学科，很多统计学家其实并不是一开始就学统计，他们都是在各自领域工作着，用着现有的统计学的方法，发现这些方法还不太行，干脆自己来干点统计工作吧，然后干着干着就成统计学家了。比如假设检验里绕不过去的人物Fisher(费舍尔)，其实就是一个生物学家，而且在生物学界还占有举足轻重的地位，是现代种群遗传学的的三杰之一。而相关系数和卡方检验的重要奠基人Person(皮尔逊)，先是在海德堡大学学习物理学，然后又到到柏林大学学法律，后来对另一个生物学家Galton(高尔顿)提出的回归分析的方法着迷，转而研究统计。

        咱们心理学学领域的学者也对统计学做了重要贡献，大家以后做问卷和学高级统计有一个绕不过去的一种方法，叫做因子分析，刚学的时候你会有疑问：“这到底是在讲啥呢？”那么这种方法是谁发明的呢，就是咱们《普通心理学》里一个赫赫有名的人物Spearman(斯皮尔曼)，Spearman用这种方法提出了自己的智力结构理论，因子分析也广泛应用在统计学界。

        咱们本文的主角Breiman也不是统计学出身，他先是在加州理工学物理，后来去伯克利学数学的，研究的概率论，大家可能觉得那不和统计差不多的吗，但其实还是有差别的，用Breiman自己的话说：“一生中我从没有学过一门统计课程。”后来因为统计学好找工作，他就去做统计工作了，后来又回到高校。在这过程中，他发现了工业界和学术界有着完全不一样的理解和应用，甚至学术界在统计学的研究上有很多地方落后于工业界，他试着把这些写下来，就有了我们的这篇文章《Statistical Modeling: The Two Cultures》。

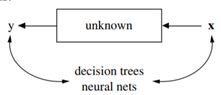
        那么这两种建模文化是哪两种文化呢，Breiman说得很清楚，一种是数据建模(Data Modeling)，一种是算法建模(Algorithmic Modeling)。当时的学术界大都以数据建模为主，而工业界已经开始运用算法建模。其实无论哪种建模，都离不开一个基本的公式y=f(x)，我们模型的目的都是在y和x之间建立联系，两种建模文化的区别就是在怎么建立联系上。Breiman用了两幅图做表示。

        第一幅是数据建模的方法，第二幅是算法建模的方法，那么两种建模方法有什么区别呢？在数据建模中，我们设定了x到y的生成过程，也就是我们设定了f()的表达式。而在算法建模中，f()是一个黑盒子，我们把y和x放进去，让它们自己生成一个最合适的f()，这其实也是机器学习和人工智能的一个比较核心的思想。

        打个比方，数据建模就是，你手里有一个x一个y，你对它们说：“我瞅你俩挺合适的，得，你俩结个婚吧。”，而算法建模就是，你手里有一个x一个y，你让他俩先谈谈恋爱，俩人找到了合适的相处方式，再结婚。

        说到这里，大家可能还觉得有点抽象，现在咱们可以用我们学过的一些统计知识打比方，其实咱们学的统计学大部分属于数据建模的方法。比如说皮尔逊相关系数(r)，其实皮尔逊相关系数是度量两个变量的线性相关程度，也就是在用皮尔逊相关系数之前，我们是假定y和x之间是有线性关系的，可以用y=a+bx的形式进行表示，这时候我们其实就是设定了f()的表达式。当r不显著的时候，我们很多人会认为x与y之间没有相关关系，但其实我们能确定的只是x与y之间可能没有线性相关关系，x和y之间还可能存在别的关系，比如y=x^2，y=x^3，这在上一篇文章中也讲过。线性回归分析中也是一样，我们假定y=a+bx，但其实y与x之间的关系究竟是不是就是线性关系其实是很难确定的，只是因为我们要用回归分析，所以我们就假设y与x是线性关系。

        Breiman用一句古语批评了数据建模：“If all a man has is a hammer, then every problem looks like a nail.”（你有一个锤子，看什么都像钉子）。

        但在Breiman看来，这还不是数据建模的最重要的问题，数据建模的最重要的问题是它的预测能力很低。就像你让x和y结婚了，但他们感情不好。Breiman讲了自己的经历，在上世纪60年代，洛杉矶深受臭氧的困扰，Breiman一行去了洛杉矶做臭氧的预测项目，帮助当地控制臭氧，他们的自变量x有450个，他们想找到x和臭氧水平y之间的关系，也就是在找f()，这时候他们选择了线性回归模型。这就是一个数据建模的过程，先假定了x与y之间存在线性关系。建模过程中，他们不断地调试模型，加入二次项和交互项，筛选自变量，但最后模型还是失败了，建立的模型都不能很好地预测臭氧水平。

        随后Breiman转向了算法建模，其实也就是我们常说的机器学习的方法，他本人在机器学习领域也颇有建树，是分类回归树，随机森林，Bagging方法的发明者，而随机森林至今也是机器学习领域表现极好的一种算法。

        算法建模兴起的一个背景是计算机的高速发展，因为每个算法背后都涉及大量的运算，算法建模最开始也不是出现在统计学界，而是由一批计算机学家和物理学家搞出来的。算法建模是把f()看作一个黑箱，我们把y与x放进去，黑箱中通过一定的算法构建出模型，比较基础和常见的算法包括决策树，支持向量机，朴素贝叶斯等，另外还有一些媒体曝光度比较高的算法，比如深度学习，神经网络。黑箱通过提供的x和y，找出一个最佳的预测路径，如果我们继续增加数据，黑箱里的模型也会根据数据发生改变。当我们数据量越来越大的时候，那么黑箱里生成的模型也就越来越靠谱。

        Breiman讲了他另一个项目经历，也是和环保局合作，这个项目是通过质谱来分析化合物中是否含氯，这次他们在尝试数据建模失败以后，果断使用了算法建模，把x和y放进去构造了决策树模型，得到了95%的预测准确性。

        毫无疑问，算法建模比数据建模的预测准确性更强，你让x与y自由恋爱，他们的感情会比被迫成婚更好。那么一个预测性好的模型可以做啥呢？这个很好理解，比如我们要判断一个人得没得癌症，有一个模型预测准确性高达99%，那么你从这个人身上收集到的各种指标放进去，就很容易判断他是不是得癌症。所以我们可以看到，对工业界来说，一个好的预测模型其实是能解决很大的问题，所以在工业界追求好的预测能力的这个趋势下，人工智能得到了如火如荼的发展。

        但其实算法建模在提升预测能力的同时，也牺牲了可解释性，在算法建模中，我们很难用一个函数表达式来概括y与x之间的关系。回到我们之前数据建模里的线性模型y=a+bx，在这个模型中，我们很容易可以看到，当x增加一个单位时，y就增加b个单位，如果这里的x是我们的自卑程度，y是我们的抑郁水平，我们就很容易解释说，自卑程度和抑郁水平呈线性相关，自卑程度增加可能提高抑郁水平，这对我们做进一步实验探索就很有指导意义。

        但是如果我们用算法建模，假设用Breiman发明的随机森林做预测，那么x可能能很好地预测y，但是我们把这个f()打开，我们会得到很多株决策树，每株决策树对结果都有贡献，我们很难解释x与y之间的具体关系，甚至连简单的x与y之间究竟是正相关还是负相关都很难判断。

        这也就是Breiman在文中说到的奥卡姆困境(OccamDilemma)，简单可解释的模型不能提供很好的预测准确性，预测准确性高的复杂模型很难被解释。随机森林在预测能力上可以得到A+的评分，但在可解释性上只有F的评分。

        Breiman在1994 年加州伯克利统计系毕业典礼上演讲的主题是：“25 年后的统计系会是什么样？”而如今已经进入了第26个年头，演讲的结尾Breiman告诉在场的同学：“记得打电话给我，让我知道 25 年后到底是如何一番景象。”但Breiman教授已经于2005年逝世，不过他的预言已经成真了，如今我们也可以看到，算法建模的思想帮助机器学习和人工智能不断发展，已经深刻地影响了我们的生活，新闻给我们推送感兴趣的内容，购物网站根据我们的喜好生成主页，包括这次疫情中对是否感染冠状病毒的判别，这些背后都有算法建模的身影。老人家如若泉下有知，亦当含笑耳。