模式识别和机器学习实战-降维算法（PCA）- Python实现 - 半导体数据进行降维处理和人脸检测

前言

降维是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。通过降维可以减少 冗余信息所造成的误差,提高识别的精度，或者通过降维算法来寻找数据内部的本质结构特征。

先介绍和解释步骤，分段介绍；最后再给出完整源码，只需修改一下文件路径即可运行。
而具体的数据集文件和代码，在如下链接里：降维算法（PCA）- Python实现

一、 降维算法

1.算法介绍

降维是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。通过降维可以减少 冗余信息所造成的误差,提高识别的精度，或者通过降维算法来寻找数据内部的本质结构特征。

2.主成分分析PCA

PCA是最常用的线性降维方法，它的目标是通过某种线性投影，将高维的数据映射到低维的空间中表示，并期望在所投影的维度上数据的方差最大，以此使用较少的数据维度，同时保留住较多的原数据点的特性。

3.在Numpy中实现PCA

将数据转换成前N个主成分的伪代码大致如下：
1.去除平均值
2.计算协方差矩阵
3.计算协方差矩阵的特征值和特征向量
4.将特征值从大到小排序
5.保留最上面的N个特征向量
6.将数据转换到上述N个特征向量构建的新空间中

主要代码如下：

二、利用PCA对半导体制造数据降维

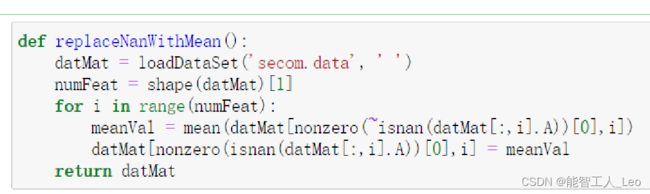
半导体制造数据很大，并且包含了590个特征。该数据包含很多的缺失值，这些缺失值是以NaN标识的，对于这些缺失值，我们用平均值来代替缺失值，平均值通过那些非NaN得到。

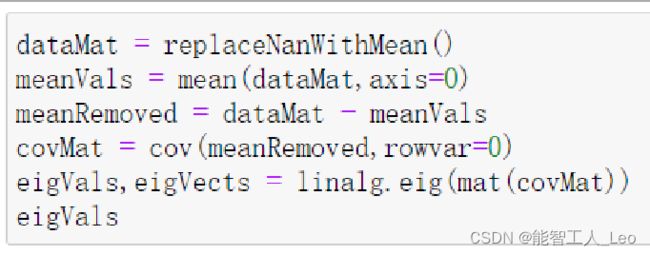
去除了所有NaN之后，接下来考虑在该数据集上应用PCA，首先确认所需特征和可以去除特征的数目。PCA会给出数据中所包含的信息量。从pca（）函数中借用以下代码来观察一下特征值的结果。

特征值的结果如下所示：有超过20%的特征值都是0；最前面15个值的数量级大于100000

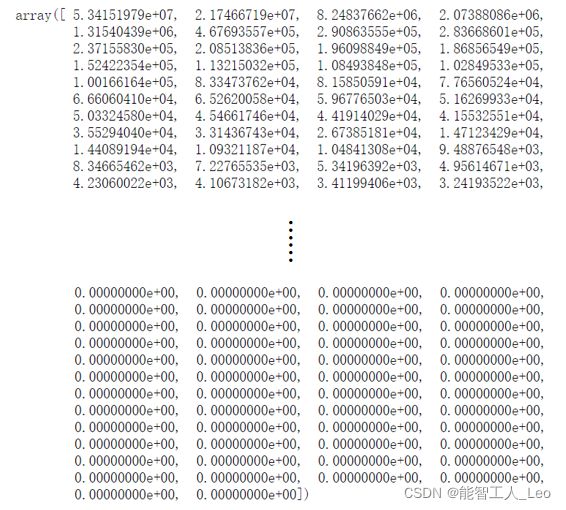
半导体数据中前7个主成分所占的方差百分比：

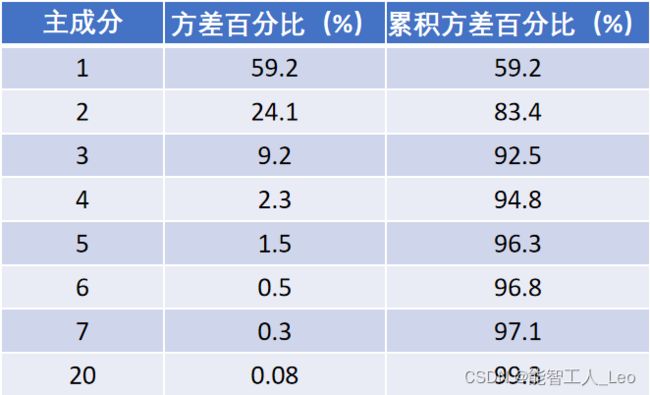
具体的主成分数目，必须通过在实验中取不同的值来确定。有效的主成分数目则取决于数据集和具体应用。
得到主成分数目之后将该属木输入到PCA算法中，降维之后的数据就可以在分类器中使用了

三、实战

1.根据之前的分析，确定半导体数据的主成分数目（可以对不同的主成分数目的降维效果进行分析），对半导体数据进行降维:

对主成分的方差占比分析，前7个主成分已经达到了97.12%，之后百分比递减，为方便计算只选取前7个降维特征。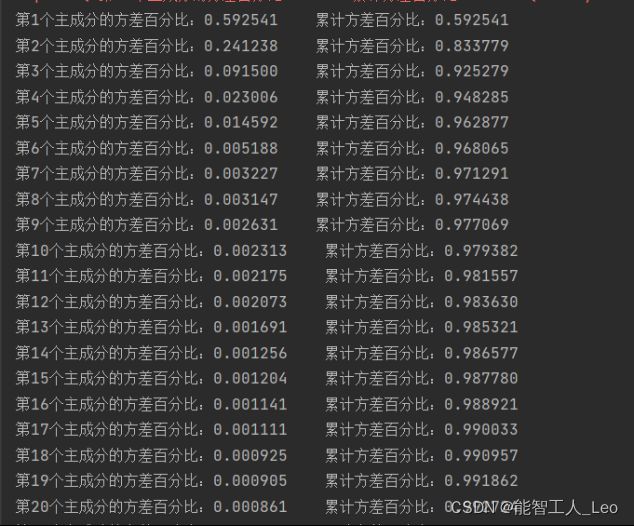

2.data-Recognition文件夹当中是yale人脸数据集（文件夹内有对于数据集的详细描述）利用主成分分析方法，选择合适的主成分数目对数据进行降维:

得到的最佳降维后数据集，如图为centerlight，取前8个主成分即可达到95%

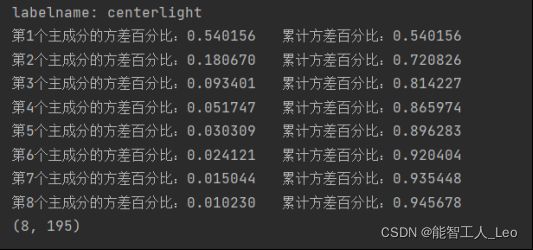
3.基于2的结果，针对data-Detection文件夹内的内容，设计一种人脸检测算法，请使用一个矩形(或正方形)来表示在给定的图像中检测到的人脸…
(利用opencv里的检测算法)

四、代码

1.主成分分析PCA

#导入数据
def loadDataSet(fileName, delim='\t'):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]
    datArr = [list(map(float, line)) for line in stringArr]
    return mat(datArr)
datamat = loadDataSet("testSet.txt")
#PCA实现
def pca(dataMat, topNfeat=9999999):
    meanVals = mean(dataMat, axis=0)  # 计算平均值
    meanRemoved = dataMat - meanVals  # 去中心化
    covMat = cov(meanRemoved, rowvar=0)  # 计算协方差矩阵
    eigVals, eigVects = linalg.eig(mat(covMat))  # 得到所有的特征值eigVals和特征向量eigVects
    eigValInd = argsort(eigVals)  # 排序
    eigValInd = eigValInd[:-(topNfeat + 1):-1]  # 保留至想要的维度
    redEigVects = eigVects[:, eigValInd]  # ...从大到小排列特征向量，得到投影矩阵
    lowDDataMat = meanRemoved * redEigVects  # 投影到新的特征空间后的数据集
    reconMat = (lowDDataMat * redEigVects.T) + meanVals  
    return lowDDataMat, reconMat
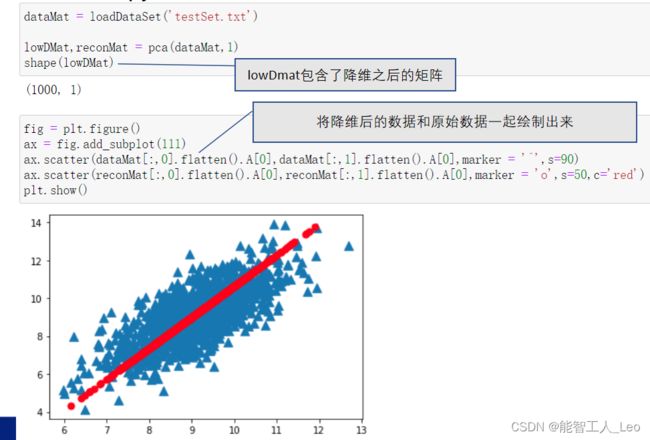
lowDDataMat, reconMat = pca(datamat, 1)

#可视化

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(datamat[:, 0].flatten().A[0], datamat[:, 1].flatten().A[0], marker='X', s=90, c='blue')
ax.scatter(reconMat[:, 0].flatten().A[0], reconMat[:, 1].flatten().A[0], marker='o', s=50, c='red')
plt.show()

2.对半导体数据进行降维处理

#对缺失值的处理，用未缺失样本的平均值代替
def replaceNaNWithMean():
    datMat = loadDataSet('secom.data', ' ')
    numFeat = shape(datMat)[1]
    for i in range(numFeat):
        meanVal = mean(datMat[nonzero(~isnan(datMat[:, i].A))[0], i])  
        datMat[nonzero(isnan(datMat[:, i].A))[0], i] = meanVal  
    return datMat

#用pca降维时，计算每个主成分的方差，获得贡献率
def PCA(dataMat, topNfeat=9999999):
    meanVals = mean(dataMat, axis=0)  # 计算平均值
    meanRemoved = dataMat - meanVals  # 去中心化
    covMat = cov(meanRemoved, rowvar=0)  # 计算协方差矩阵
    eigVals, eigVects = linalg.eig(mat(covMat))  # 得到所有的特征值eigVals和特征向量eigVects
    eigValInd = argsort(eigVals)  # 排序
    eigValInd = eigValInd[:-(topNfeat + 1):-1]  # 保留至想要的维度
    redEigVects = eigVects[:, eigValInd]  # ...从大到小排列特征向量
    lowDDataMat = meanRemoved * redEigVects  # 投影到新的特征空间后的数据集
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    tot = sum(eigVals)  # 计算特征值的和
    var_exp = [(i / tot) for i in sorted(eigVals, reverse=True)]  # 按照降序排列特征值，并计算贡献率
    cum_var_exp = cumsum(var_exp)  # 累计贡献度
    for i in range(len(var_exp)):
    print("第%d个主成分的方差百分比：%f    累计方差百分比：%f" % (i + 1,   
					float(var_exp[i]),float(cum_var_exp[i])))  # 输出贡献度

    return lowDDataMat, reconMat

#调用pca获得降维后的前七个主成分数据集
dataMat = replaceNaNWithMean()
lowDDataMat, reconMat = PCA(dataMat, 7)  #前7个主成分所占的方差已经累计达97.1%
print(lowDDataMat)  #得到降维后的数据集
print("数据集个数：%d"% shape(lowDDataMat)[0],"主成分个数：%d"% shape(lowDDataMat)[1])

3.人脸检测算法

from numpy import *
import cv2
import os
import matplotlib.pyplot as plt
import matplotlib.image as mpimg

def loaddata():
    data = []
    label = ["centerlight", "glasses", "happy", "leftlight", "noglasses", "normal", "rightlight", "sad", "sleepy","surprised", "wink"]
    for i in range(15):
        data.append({})
        for j in label:
            h = str(i + 1)
            if i < 9:
                h = "0" + h
            data[i][j] = mpimg.imread("project1-data-Recognition1//subject{}.{}.pgm".format(h, j))
    return data, label  # 数据集和标签


def PCA(dataMat, topNfeat=999999):
    meanVals = mean(dataMat, axis=0)  # 计算平均值
    meanRemoved = dataMat - meanVals  # 去中心化
    covMat = cov(meanRemoved, rowvar=0)  # 计算协方差矩阵
    eigVals, eigVects = linalg.eig(mat(covMat))  # 得到所有的特征值eigVals和特征向量eigVects
    eigValInd = argsort(eigVals)  # 排序
    eigValInd = eigValInd[:-(topNfeat + 1):-1]  # 保留至想要的维度
    redEigVects = eigVects[:, eigValInd]  # ...从大到小排列特征向量
    lowDDataMat = meanRemoved * redEigVects  # 投影到新的特征空间后的数据集
    reconMat = (lowDDataMat * redEigVects.T) + meanVals

    tot = sum(eigVals)  # 计算特征值的和
    var_exp = [(i / tot) for i in sorted(eigVals, reverse=True)]  # 按照降序排列特征值，并计算贡献率
    cum_var_exp = cumsum(var_exp)  # 累计贡献度
    for i in range(len(var_exp)):
        if float(cum_var_exp[i]) < 0.95:
            print("第%d个主成分的方差百分比：%f   累计方差百分比：%f" % (i + 1, float(var_exp[i]), float(cum_var_exp[i])))  # 输出贡献度
        else:
            break
    return lowDDataMat[:i], reconMat[:i]  #返回我们需要的维度的数据集


datamat, label = loaddata()

def subjectDataMat():  # 得到所有数据降维后的数据集
    subjectDataMat = []
    for i in label:
        print("\nlabelname: %s " % i)
        lowDDataMat, reconMat = PCA(datamat[0][i])
        subjectDataMat.append(lowDDataMat)
    return subjectDataMat


def traingdata(N):  # 获得训练集，N为输入的个数3,5,7...
    traingdata=[]
    for i in label:
        for j in range(N):  # 随机选择N个
            num = random.randint(1, 11)
            traingdata.append(datamat[0][i][num])
    lowDtraingdata, recontraingdata = PCA(traingdata)
    return lowDtraingdata

datamat, label = loaddata()
traingdata(3)