机器学习笔记--TensorFlow学习笔记(3)--MNIST机器学习入门

机器学习的入门：使用MNIST数据集识别手写数字。

0.导入

使用tensorflow之前，首先导入它

import tensorflow as tf

导入mnist数据

from tensorflow.examples.tutorials.mnist import input_data
mnist=input_data.read_data_sets('MNIST_data',one_hot=True)

MNIST是一个入门级的计算机视觉数据集，它包含各种手写数字图片，它也包含每一张图片对应的标签，告诉我们这个是数字几。下载下来的数据集被分成两部分：60000行的训练数据集（mnist.train）和10000行的测试数据集（mnist.test）。
正如前面提到的一样，每一个MNIST数据单元有两部分组成：一张包含手写数字的图片和一个对应的标签。我们把这些图片设为“xs”，把这些标签设为“ys”。训练数据集和测试数据集都包含xs和ys，比如训练数据集的图片是 mnist.train.images ，训练数据集的标签是 mnist.train.labels。
每一张图片包含28X28个像素点。我们可以用一个数字数组来表示这张图片，我们把这个数组展开成一个向量，长度是 28x28 = 784。如何展开这个数组（数字间的顺序）不重要，只要保持各个图片采用相同的方式展开。

1.设置变量

通过操作符号变量来描述这些可交互的操作单元

x = tf.placeholder(tf.float32, [None, 784])

x是一个占位符，用2维的浮点数张量表示这些图，张量的形状是[None, 784],None表示此张量的第一维可以是任意长度

Variable代表可修改的张量 模型参数w,b

W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

2.建立模型

这是一个使用softmax回归（softmax regression）模型的经典案例。softmax模型可以用来给不同的对象分配概率。
softmax回归（softmax regression）分两步：
第一步：
evidence:

第二步：

其中，

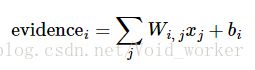
y = tf.nn.softmax(tf.matmul(x, W) + b)

用matmul(x, W)计算Wx，然后加上b，再将和输入到tf.nn.softmax函数里面

3.训练模型

3.1 定义指标来评估模型

通常定义指标来表示一个模型是坏的：成本(cost)或损失(loss)，然后最小化这个指标
一个常见的成本函数：交叉熵(cross-entropy):交叉熵是用来衡量我们的预测用于描述真相的低效性。
交叉熵函数：

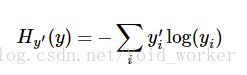
y_ = tf.placeholder("float", [None, 10])

y_ 表示正确值

cross_entropy = -tf.reduce_sum(y_ * tf.log(y))

用tf.log计算y的每个元素的对数，然后与y_对应元素相乘，最后，用tf.reduce_sum计算张量的所有元素之和

3.2 设置优化算法最小化成本函数

因为TensorFlow拥有一张描述各个计算单元的图，它可以自动地使用反向传播算法(backpropagation algorithm)
来有效地确定你的变量是如何影响你想要最小化的那个成本值的。然后，TensorFlow会用你选择的优化算法来不断地修改变量以降低成本。

train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

使用梯度下降算法(Gradient Descent Algorithm)：将每个变量一点点地往使成本不断降低的方向移动
以0.01的学习速率最小化交叉熵

3.3 初始化变量

init = tf.initialize_all_variables()

3.4 启动模型

sess = tf.Session()
sess.run(init)

3.5 训练模型

for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict = {x:batch_xs, y_: batch_ys})

让模型循环训练1000次
该循环的每个步骤中，随机抓取训练数据中的100个批处理数据点，用这些数据点作为参数替换之前的占位符来运行train_step。
随机梯度下降训练:使用一小部分的随机数据来进行训练,减少计算开销，又可以最大化地学习到数据集的总体特性。

4.评估模型

correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))

tf.argmax函数能给出某个tensor对象在某一维上的其数据最大值所在的索引值
tf.argmax(y, 1)返回模型对于任一输入x预测到的标签值，tf.argmax(y_, 1)代表正确的标签
tf.equal检测索引位置是否一致

accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))

accuracy:对预测到的值取平均值，如：[True, False, True, True]变成[1,0,1,1],取平均值后得到0.75

print(sess.run(accuracy, feed_dict = {x:mnist.test.images, y_:mnist.test.labels}) )

最终结果：accuracy =

5.总代码

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

'使用MNIST 进行手写数字识别'

__author__ = 'VoidWalker'

# 0.导入
# 使用tensorflow之前，首先导入它
import tensorflow as tf
# 导入mnist数据
from tensorflow.examples.tutorials.mnist import input_data
mnist=input_data.read_data_sets('MNIST_data',one_hot=True)


# 1.设置变量
# 通过操作符号变量来描述这些可交互的操作单元
x = tf.placeholder(tf.float32, [None, 784])
# x是一个占位符，用2维的浮点数张量表示这些图，张量的形状是[None, 784],None表示此张量的第一维可以是任意长度

# Variable代表可修改的张量 模型参数w,b
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))

# 2.建立模型
y = tf.nn.softmax(tf.matmul(x, W) + b)
# 用matmul(x, W)计算Wx，然后加上b，再将和输入到tf.nn.softmax函数里面

# 3.训练模型
# 3.1 定义指标来评估模型
# 通常定义指标来表示一个模型是坏的：成本(cost)或损失(loss)，然后最小化这个指标
# 一个常见的成本函数：交叉熵(cross-entropy):交叉熵是用来衡量我们的预测用于描述真相的低效性。
y_ = tf.placeholder("float", [None, 10])
# y_ 表示正确值
cross_entropy = -tf.reduce_sum(y_ * tf.log(y))
# 用tf.log计算y的每个元素的对数，然后与y_对应元素相乘，最后，用tf.reduce_sum计算张量的所有元素之和

# 3.2 设置优化算法最小化成本函数
# 因为TensorFlow拥有一张描述你各个计算单元的图，它可以自动地使用反向传播算法(backpropagation algorithm)
# 来有效地确定你的变量是如何影响你想要最小化的那个成本值的。然后，TensorFlow会用你选择的优化算法来不断地修改变量以降低成本。
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)
# 使用梯度下降算法(Gradient Descent Algorithm)：将每个变量一点点地往使成本不断降低的方向移动
# 以0.01的学习速率最小化交叉熵

# 4.0 初始化变量
init = tf.initialize_all_variables()

# 4.1 启动模型
sess = tf.Session()
sess.run(init)

# 4.2训练模型
for i in range(1000):
    batch_xs, batch_ys = mnist.train.next_batch(100)
    sess.run(train_step, feed_dict = {x:batch_xs, y_: batch_ys})
# 让模型循环训练1000次
# 该循环的每个步骤中，随机抓取训练数据中的100个批处理数据点，用这些数据点作为参数替换之前的占位符来运行train_step。
# 随机梯度下降训练:使用一小部分的随机数据来进行训练,减少计算开销，又可以最大化地学习到数据集的总体特性。

# 5.评估模型
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
# tf.argmax函数能给出某个tensor对象在某一维上的其数据最大值所在的索引值
# tf.argmax(y, 1)返回模型对于任一输入x预测到的标签值，tf.argmax(y_, 1)代表正确的标签
# tf.equal检测索引位置是否一致
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
# accuracy:对预测到的值取平均值，如：[True, False, True, True]变成[1,0,1,1],取平均值后得到0.75
print(sess.run(accuracy, feed_dict = {x:mnist.test.images, y_:mnist.test.labels})