一文读懂特征值分解EVD与奇异值分解SVD

这篇关于特征值和特征向量的内容是我用PCA的时候接触到的，本科学的东西早就记不得了orz，所以复习了一遍顺便做了一下梳理，这算是PCA的前置知识。

特征值分解

特征值与特征向量

设 $A$ 是 $n$ 阶矩阵, 如果数$\lambda$ 和 $n$ 维非零列向量 $x$ 使关系式
$$Ax=\lambda x$$成立，那么$\lambda$ 就称为矩阵 $A$ 的特征值, $x$ 称为$A$的对应于特征 值 $\lambda$ 的特征向量。

注意有两个要素：（1）$A$是方阵（2）$x$是非零向量

我们都知道左乘矩阵代表的是线性变换，上述定义从几何来理解就是：向量 $x$ 经过$A$变换后，它的方向没有变（可能会相反），而大小变为$\lambda$倍。这是一种很特殊的情况，你想变换后的向量形式千千万，唯独某类向量会保持住它的方向不变，而只改变其长度，这类向量对$A$来说是及其特殊的存在，所以我们可以认为矩阵$A$的特征可以由这些特征值和对应的特征向量所体现（这可能是“特征”两字的由来）。

定义可以写成： $$(A-\lambda E)x=0$$这是一个齐次线性方程组，它有非零解的充分必要条件是系数行列式等于0，也就是$$|A-\lambda E|=0$$这个式子化简以后是以 $\lambda$ 为未知数的一元 $n$ 次方程，称为矩阵 $A$ 的特征方程，它有$n$个解（重根解算多个），这些解就是矩阵$A$的特征值，求出特征值再带回到第二个式子中就可以得到对应的特征值$x$。
关于这$n$个解，有三种情况

1. 存在复数解
2. 都是实数解，但存在重根
3. 都是互异实数解

下文都不考虑复数解的情况，先举个求特征值和特征向量的例子：
求矩阵 $A=\left(\begin{array}{rr}3& -1\\ -1& 3\end{array}\right)$ 的特征值和特征问量
特征多项式为：
$$|A-\lambda E|=\left|\begin{array}{cc}3-\lambda & -1\\ -1& 3-\lambda \end{array}\right|=(3-\lambda {)}^2-1=8-6\lambda +{\lambda }^2=(4-\lambda )(2-\lambda )$$所以 A 的特征值为 ${\lambda }_1=2,{\lambda }_2=4$，当 ${\lambda }_1=2$ 时, 对应的特征向量应满足
$$\left(\begin{array}{cc}3-2& -1\\ -1& 3-2\end{array}\right)\left(\begin{array}{l}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{l}0\\ 0\end{array}\right)$$即$$\left(\begin{array}{rr}1& -1\\ -1& 1\end{array}\right)\left(\begin{array}{l}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{l}0\\ 0\end{array}\right)$$解得$$p_1=k\left(\begin{array}{l}1\\ 1\end{array}\right)（k\ne 0）$$同理可以求出${\lambda }_2=4$时对应的特征向量，从这个例子我们可以看到，特征向量是不唯一的。
那么特征值具有哪些性质呢？如下：

1. ${\lambda }_1+{\lambda }_2+\cdots +{\lambda }_n=a_{11}+a_{22}+\cdots +a_{nn}$
2. ${\lambda }_1{\lambda }_2\cdots {\lambda }_n=|\mathbf{A}|$
3. $\phi (\lambda )$ 是 $\phi (A)$ 的特征值，其中 $\phi (\lambda )=a_0+a_1\lambda +\cdots +a_m{\lambda }^m$ 是 $\lambda$ 的多项式 , $\phi (A)=a_{0}E+a_{1}A+\cdots +a_m{A}^m$是矩阵$A$的多项式，由此可以得到两个特殊的，(1) ${\lambda }^k$ 是 $A^k$ 的特征值（2）$\frac{1}{\lambda }$ 是 ${\mathbf{A}}^{-1}$ 的特征值
4. 不同特征值对应的特征向量线性无关

特征值分解

先引入一个相似矩阵的概念，定义，设$A、B$都是$n$阶矩阵，若有可逆矩阵$P$，使
$$P^{-1}AP=B$$则称$A$与$B$相似，这个过程称为相似变换，$P$称为相似变换矩阵。
它具有一个很重要的性质：相似矩阵的特征值相同

为什么要引入这么一个东西？主要是为了引出相似对角化这个玩意。
特殊的，如果$A$与对角矩阵$\mathbf{\Lambda }=\left(\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right)$相似，即$P^{-1}AP=\Lambda$ 那么${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n$ 是 $A$ 的 $n$ 个特征值（相似矩阵和对角矩阵的性质），而 $P$ 的列向量 $p_i$ 就是 $A$ 的对应于特征值${\lambda }_i$的特征向量。

把$P$乘到右边，得到：
$$A=P\Lambda P^{-1}$$
这个式子就是实际中经常用到的特征值分解，一个矩阵$A$可以通过特征值分解得到它的特征值和特征向量（numpy有包可以直接调用） ，但是特征分解只适用于方阵，更普遍的是奇异值分解SVD。

import numpy as np
from numpy.linalg import eig

a = np.array([[1, 2, 3],[5, 8, 7],[1, 1, 1]])
e_vals,e_vecs = np.linalg.eig(a)

print(e_vals)
print(e_vecs)
# 注意列向量才是特征向量
[10.254515   -0.76464793  0.51013292]
[[-0.24970571 -0.89654947  0.54032982]
 [-0.95946634  0.19306928 -0.73818337]
 [-0.13065753  0.39865186  0.40389232]]

从相似对角化的的定义可以看到，我们可以把一个复杂的矩阵$A$变换成一个很简单的对角矩阵，而这个对角矩阵也同样保留了原来矩阵的特征，且变换的矩阵$P$就是$A$的特征向量组成的矩阵，挺神奇！把一个复杂的事物变成具有同样性质的简单事物，进一步我们可以用这个简单的事物代替复杂的事物去做一些操作，从而提高效率或减少复杂度，这在工程上是非常有用的。

但是注意，不是每一个矩阵都能与对角矩阵相似，首先注意到$P$必须是可逆的，而$P$又是由特征向量组成，那么换句话说：当且仅当$A$有$n$个线性无关的特征向量时，$A$才能相似对角化。由这个定理结合特征值的性质4我们可以得到推论：如 果 $n$ 阶 矩 阵 $A$ 的 $n$ 个特征值互不相等（解的情况3） , 则 $A$ 可以相似对角化。

那么哪些不可以相似对角化？解的情况2中，重根对应的特征向量个数小于重数的矩阵，比如矩阵$A=\left(\begin{array}{rrr}-1& 1& 0\\ -4& 3& 0\\ 1& 0& 2\end{array}\right)$，$\lambda =1$是2重根（另外一个根是2），但是对应的线性无关的特征向量只有一个，所以总体上就只有2个线性无关的特征向量（ < 3），故不能相似对角化。

对称矩阵的特征值分解

在可相似对角化的矩阵中，对称矩阵（$A^T=A$）是经常用到，它的性质是：对称矩阵都有 N 个线性无关的特征向量，且不同特征值对应的特征向量相互正交。

由此我们可以知道，对称矩阵一定可以相似对角化，而且可以把些特征向量正交单位化而得到一组正交且模为 1 的向量，故实对称矩阵 A 可被分解成：

$$A=P\Lambda P^{-1}=PA{P}^{\mathrm{T}}$$
其中，$P$为正交矩阵（$P{P}^T=E$）

奇异值分解SVD

特征值分解是一个提取矩阵特征很不错的方法，但是它只是对方阵而言的，在现实的世界中，我们看到的大部分矩阵都不是方阵，那么奇异值分解就是一种能适用于任意矩阵分解的方法。

假设矩阵A是一个 $m\times n$ 的矩阵，那么就可以分解为：
$$A=U\Sigma V^T$$
U： $m\times m$ ，其中的列向量 $u_1,u_2,\dots ,u_m$ 是 $A{A}^T$ 的特征向量, 称为矩阵 $A$的左奇异向量。
V： $n\times n$ ,其中的列向量 $v_1,v_2,\dots ,v_m$ 是 $A^{T}A$ 的特征向量, 称为矩阵 $A$的右奇异向量。
$\Sigma$：$m\times n$ ，除了主对角线上的元素以外全为0， 主对角线上的元素${\sigma }_i$称为奇异值,${\sigma }_i=\sqrt{{\lambda }_i}$，${\lambda }_i$是$A^{T}A$的特征值（或$A{A}^T$，两者特征值相同）。
另外，U和V都是正交矩阵（因为它们是对称矩阵求出来的呀！）, 即满足 $U^{T}U=E,V^{T}V=E$。
示意图如下：

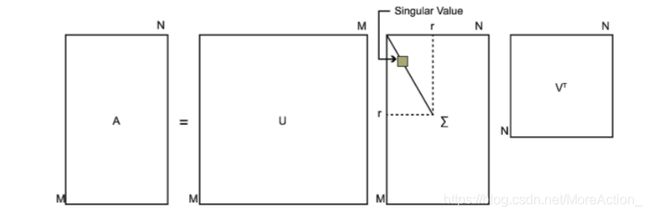
奇异值在矩阵中是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：
$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\approx U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T$$
其中，k是一个远小于m、n的数。SVD具有的这种特性可以用于PCA降维、数据压缩和去噪等，关于PCA的内容会另写一篇博客。

reference
<<工程数学线性代数第六版>>
<<线性代数及其应用>>
https://www.zhihu.com/question/21874816/answer/181864044
https://blog.csdn.net/itnerd/article/details/83445155
https://www.cnblogs.com/pinard/p/6251584.html

如果对你有帮助，请点个赞让我知道:-D