数据集:各地区化妆品销量、人口数量和人均收入
数据集:各地区化妆品销量、适用人数和人均收入
本文研究二元线性回归分析。
1. 数据表
| 地区i | 销量(箱)yi | 人口(千人) xi1 | 人均收入(元)xi2 |
|---|---|---|---|
| 1 | 162 | 274 | 2450 |
| 2 | 120 | 180 | 3254 |
| 3 | 223 | 375 | 3802 |
| 4 | 131 | 205 | 2838 |
| 5 | 67 | 86 | 2347 |
| 6 | 169 | 265 | 3782 |
| 7 | 81 | 98 | 3008 |
| 8 | 192 | 330 | 2450 |
| 9 | 116 | 195 | 2137 |
| 10 | 55 | 53 | 2560 |
| 11 | 252 | 430 | 4020 |
| 12 | 232 | 372 | 4427 |
| 13 | 144 | 236 | 2660 |
| 14 | 103 | 157 | 2088 |
| 15 | 212 | 370 | 2605 |
先将数据保存为
2.1.xlsx.
2. 数据预处理
2.1 导包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.formula.api import ols # 线性回归
2.2 读取数据
data = pd.read_excel('2.1.xlsx')
2.3 规范字段信息(便于绘图显示)
data=data.rename(columns={' 地区i':'i','销量(箱)yi':'Y','人口(千人) xi1':'X1','人均收入(元)xi2':'X2'})
print(data) # 预览字段信息修改后的数据
结果:
i Y X1 X2
0 1 162 274 2450
1 2 120 180 3254
2 3 223 375 3802
3 4 131 205 2838
4 5 67 86 2347
5 6 169 265 3782
6 7 81 98 3008
7 8 192 330 2450
8 9 116 195 2137
9 10 55 53 2560
10 11 252 430 4020
11 12 232 372 4427
12 13 144 236 2660
13 14 103 157 2088
14 15 212 370 2605
3. 数据描述性分析
describe = data.describe()
print(describe)
结果:
i Y X1 X2
count 15.000000 15.000000 15.000000 15.000000
mean 8.000000 150.600000 241.733333 2961.866667
std 4.472136 62.049289 116.829831 730.636500
min 1.000000 55.000000 53.000000 2088.000000
25% 4.500000 109.500000 168.500000 2450.000000
50% 8.000000 144.000000 236.000000 2660.000000
75% 11.500000 202.000000 350.000000 3518.000000
max 15.000000 252.000000 430.000000 4427.000000
4. 自变量与因变量线性关系预判断
plt.figure(1);
plt.scatter(data['X1'],data['Y']);
plt.xlabel('$X_1$');
plt.ylabel('$Y$');
plt.title('$X_1-Y$')
plt.figure(2);
plt.scatter(data['X2'],data['Y']);
plt.xlabel('$X_2$');
plt.ylabel('$Y$');
plt.title('$X_2-Y$')
plt.ioff();
plt.show();
图示:
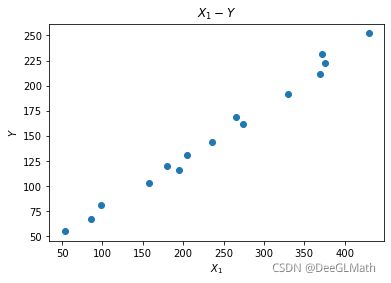
X 1 − Y X_1-Y X1−Y:各地区化妆品销量与人口数量有明显的线性相关性,说明化妆品销量与人口数量成正相关性。
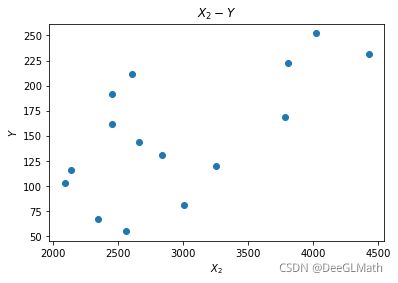
X 2 − Y X_2-Y X2−Y:各地区化妆品销量与人均收入没有明显的线性相关性,说明各地区居民经济实力并不显著影响化妆品销量。
5. 计算相关系数
print(data[['Y','X1','X2']].corr())
结果:
Y X1 X2
Y 1.000000 0.995492 0.639301
X1 0.995492 1.000000 0.568560
X2 0.639301 0.568560 1.000000
结论:
各地区化妆品销量与人口数量有很强的正相关性,各地区化妆品销量与人均收入没有很强的正相关性。
6. 二元线性回归分析
# 可以调用sklearn中的LinearRegression
lm = ols('Y ~ X1 + X2', data=data).fit()
print(lm.summary())
结果:
OLS Regression Results
==============================================================================
Dep. Variable: Y R-squared: 0.999
Model: OLS Adj. R-squared: 0.999
Method: Least Squares F-statistic: 5679.
Date: Thu, 30 Sep 2021 Prob (F-statistic): 1.38e-18
Time: 17:36:11 Log-Likelihood: -31.281
No. Observations: 15 AIC: 68.56
Df Residuals: 12 BIC: 70.69
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 3.4526 2.431 1.420 0.181 -1.843 8.749
X1 0.4960 0.006 81.924 0.000 0.483 0.509
X2 0.0092 0.001 9.502 0.000 0.007 0.011
==============================================================================
Omnibus: 0.227 Durbin-Watson: 2.701
Prob(Omnibus): 0.893 Jarque-Bera (JB): 0.412
Skew: -0.115 Prob(JB): 0.814
Kurtosis: 2.221 Cond. No. 1.32e+04
==============================================================================
参数含义参照表
6.1 回归分析,模型检验,系数检验
模型检验:
- 根据决定系数 R 2 R^2 R2的值,即:
R-squared: 0.999
该模型的显著性较好。
- 根据 F F F检验的结果:
Prob (F-statistic): 1.38e-18
取 α = 0.05 \alpha=0.05 α=0.05,由于 1.38 e − 18 < α 1.38e-18<\alpha 1.38e−18<α,故拒绝原假设( H 0 H_0 H0:模型不是显著的),即认为模型是显著的。
系数检验:
coef
X1 0.4960
X2 0.0092
观察P>|t|的两个值,均为0.000,由于小于置信水平,通常为0.05,则表明系数在统计上具有显著的关系。
6.2 多重共线性检验, DW检验
- 根据两个变量相关系数的结果:0.568560,可以大致看出,变量间没有很强的多重共线性。
- 根据Durbin-Watson的结果:2.701,可以得出该值在2左右,残差符合正态分布。
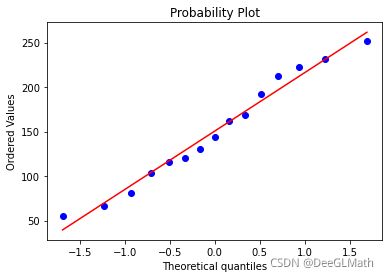
from scipy import stats
res = stats.probplot(data['Y'],plot=plt)