【人工智能数学：01概率论】（2） 离散型概率空间
一、说明
这篇文章是对概率空间最基本概念的描述。解决的基本问题是试图“说服”大家，概率空间是个啥。不解决这种基本问题，试图提高学术水平是不可能的。
本文将涉及概率空间的定义、对于离散概率事件的定义、连续概率事件的定义、
代数的一些含义、测度的概念，以及它们如何被引入，如何满足实践问题以补救古典概率的不足。
二、从概率空间说起
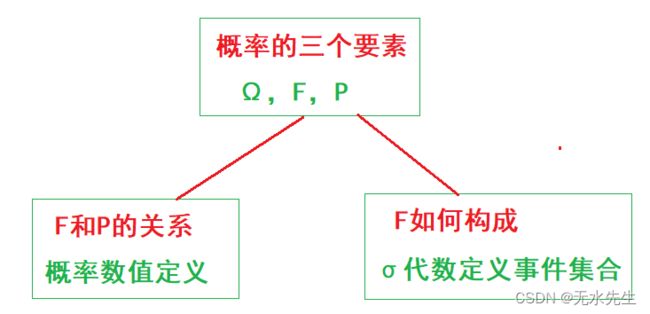
我们以下所说的概率空间。其内容概括为下图：
2.1 概率空间
1）概率三要素
概率空间存在三个基本组成，
，其中：
是样本的集合，
是事件的集合，
是概率，是事件的数对应（号称概率）一般写成
,其中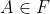
。
Ω 是一个非空集合 ，有时称作“样本空间”，就是最基本的事件符号构成的集合。
也是样本点的集合，是所包含的所有事件的母集合，也就是说，F中所有事件，都通过Ω集合产生。Ω样本元素必出现在F中，不能多，也不能少。（注：每个样本点需要互斥，样本点必须被穷举。这意味着，对于连续概率函数需要可数化，这些将在下一篇描述）
什么是事件？凡是的子集都可以构成一个事件，这里强调，事件是用一个集合描述。
2）事件与概率的关系
以上是对概率空间三要素的基本解释，然而，对于以上概率空间要素，必须要有以下几个约束，才能构成概率空间的定义：
1）对于，
2)
,对于不可能事件（空事件），概率为0
3)
，对所有可能事件（这些事件是“或”的关系），发生概率是1
4）对于一组互斥事件，概率可以相加，
是互斥事件，
2.2 实践概率空间
1）0-1分布概率空间
【例1】对于最简单的0-1分布的概率空间，假定，抛硬币，正面概率0.6，反面概率0.4，写出概率空间的表示：
事件定义：正面1，反面0
所以：
这里密切注意：和的区别！
2）对骰子定义概率空间
【例2】为了说明问题，这里引用四面体的骰子，写出概率空间的表示：
事件定义：1，2，3，4
所以：
对于事件情况就复杂了，对于四面体骰子，抛出1，2，3，4是一个基本事件，这没有问题，但是，如果【抛出偶数】这也是一个事件，应该是事件A=【2，4】也是一个事件，更一般的，抛出【1，2】（1或2）也能算作一个事件，把这些事件写全了是什么呢？答案是16个：
F = { Φ，{1}，{2}，{3}，{4}，{1，2}，{1，3}，{1，4}，{2，3}，{2，4}，{3，4}，{1，2，3}，{1，2，4}，{1，3，4}，{2，3，4}，{1，2，3，4} }
事件对应的概率：
P = [0,1/4,1/4,1/4,1/4,1/2,1/2.1/2,1/2,1/2.3/4,3/4,3/4,3/4,1]
注意：F是Ω的划分，以上列出全部的划分组成的事件，对于实际问题，可以按照σ代数的原则进行有选择的划分，构成独特的概率空间。
三、 按照σ代数构造事件集合
3.1 关于σ代数
这里依然引用四面体的骰子，模型构造出一个合理的概率空间。
用符号表示事件: 1, 2，3，4
所以：Ω={1，2，3，4}
F = { Φ，{1}，{2}，{3}，{4}，{1，2}，{1，3}，{1，4}，{2，3}，{2，4}，{3，4}，{1，2，3}，{1，2，4}，{1，3，4}，{2，3，4}，{1，2，3，4} } （1）
注意：这里定义了一个最大事件集族。下面描述更一般的定义。
1）σ代数
将以上结论上升到σ代数理论，有下列规定：对于集合Ω的子集组成的集合F满足：
- 对于 A∈F，那么
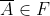也成立。 - 对于 A∈F和B∈F，那么A∪B∈F也成立。
- 于是 F就是一个σ代数。
按照定义，以上式（1）构成一个σ代数，而且是以Ω为基础构建的最大σ代数。而式1）这个σ代数的子代数，也构成一个σ代数，所有这些σ代数都可以构成概率空间。
2）概率空间示例
举例说明，下面都可以成为概率空间：Ω={1，2，3，4}
1）F={Φ，{1}，{2，3，4}，{1，2，3，4 } }
2）F = {Φ，{1}，{2}，{1，2}，{3，4}，{1，3，4}，{2，3，4}，{1，2，3，4}}
3）F = {Φ，{1，2}，{3，4}，{1，2，3，4} }
以上构成的F事件都存在确定概率P，可以组成概率空间。
（后续博文：关于连续函数如何定义概率空间？）