李宏毅2022《机器学习/深度学习》——学习笔记（5）

优化方法

常用的优化方法

CNN

CNN和全连接神经网络的区别

全连接神经网络的每个神经元和每一个输入都有连接，这样会使训练参数数目很大。

考虑到图片分类的特性，实际上每一个神经网络只需要和部分输入连接就行。

由于人在识别图片中某个物体其实只是看图片中某些特征，比如看一只鸟，当看到了鸟喙、鸟的眼睛和鸟爪，就能判断这张图片代表的是一只鸟。因此一个神经元只看输入的某一块区域，当发现一些特征时，就可以判断这个物体的类别了。所以不需要每个神经元都去看一张完整的图片。

感受野

下面就可以做简化

本来一个神经元会看整个图片，也就是和3长宽的输入相连，现在设置一个感受野，让神经元只和这一个感受野中的输入相连。具体来说，如上图所示，把这个感受野中的数据拉直，也就是333个输入，让它们和神经元相连，这样就有27个权重，再加上bias，计算结果送给下一个神经元。

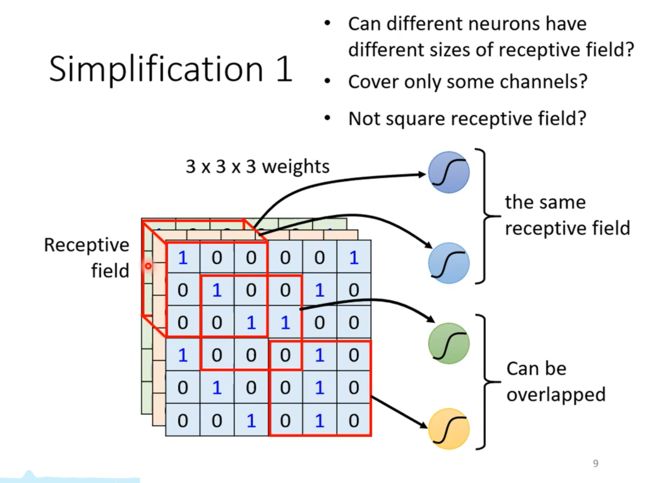
感受野的设计完全由自己决定，不过要和实际情况和对问题的理解结合。

一种经典的设计方式

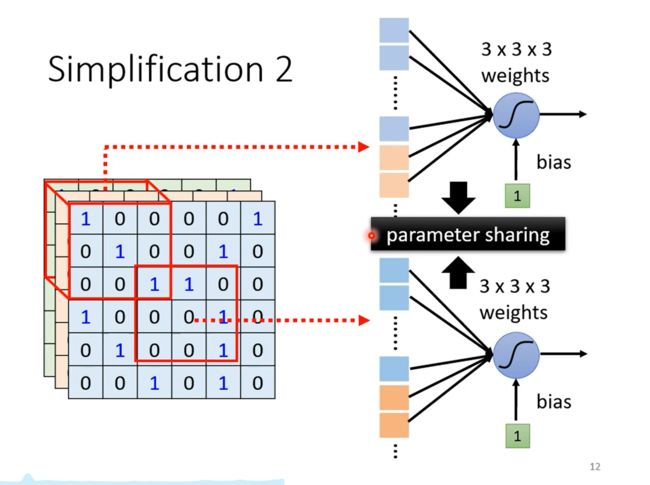
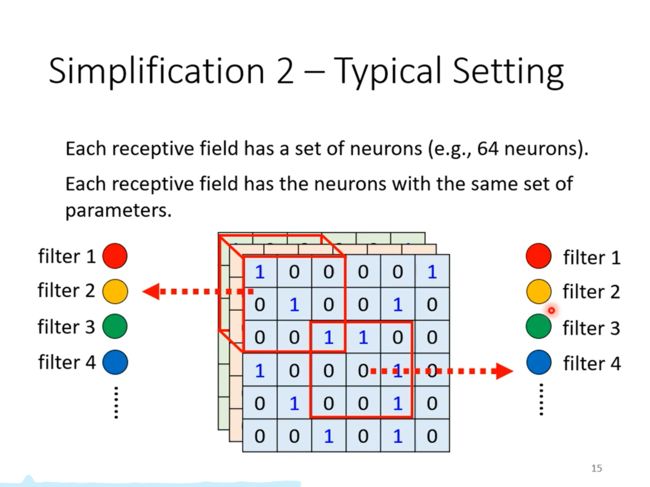
共享参数

同样的pattern可能出现在图片的不同区域

这些侦测鸟嘴的神经元所做的事情是一样的，只是它们守备的范围不同，那就没有必要每个侦测鸟嘴的地方都放一个神经元，这样可以减少参数。

这样就可以共享参数

这两个神经元的权重完全是一样的

一个典型的设计
每个神经元都只有一组参数

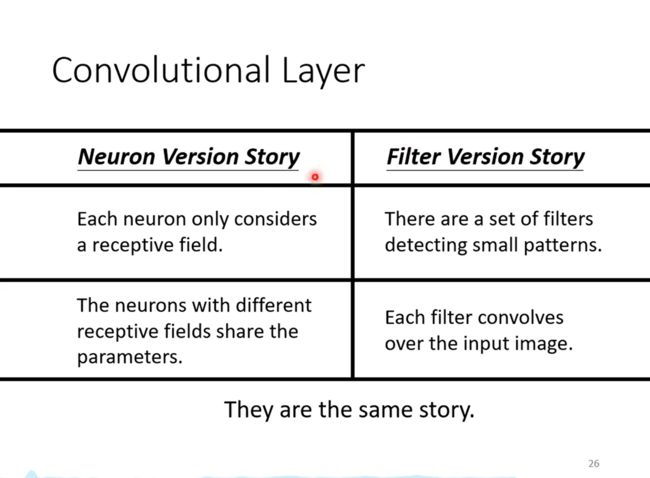
CNN和全连接神经网络的总结

全连接神经网络加上稀疏连接和权值共享就变成了CNN

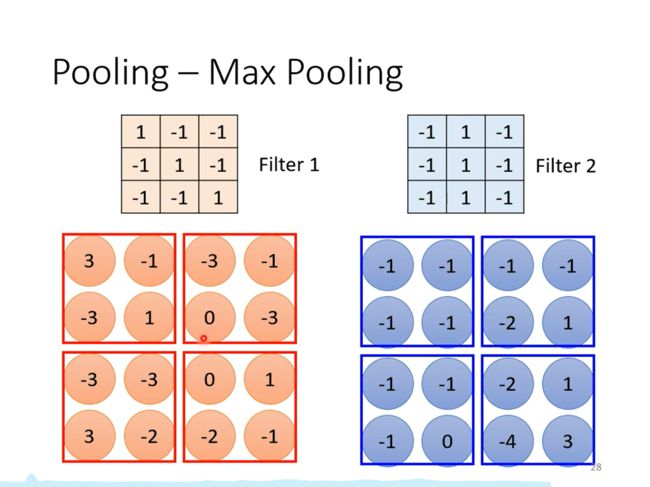
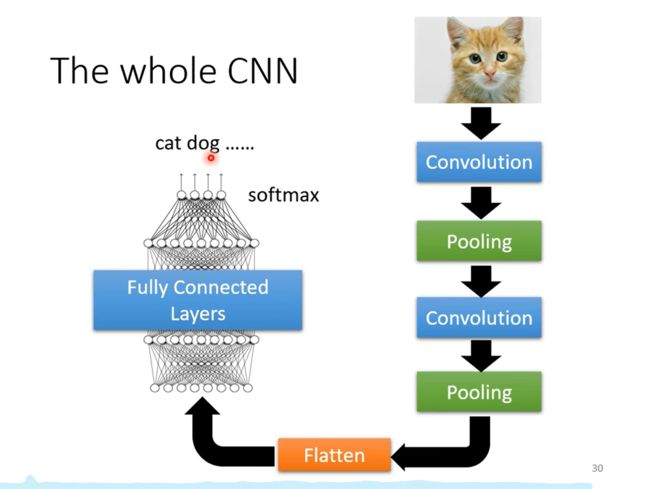
Pooling

CNN流程

自注意力机制

自注意力机制解决的问题

目前我们遇到的问题，输入都是一个向量，输出是一个数值或类别。
但是可能遇到另一种问题，输入是一组长度不确定的向量，这种情况如何处理？
自注意力机制（Slef-attention）就是要解决这个问题。

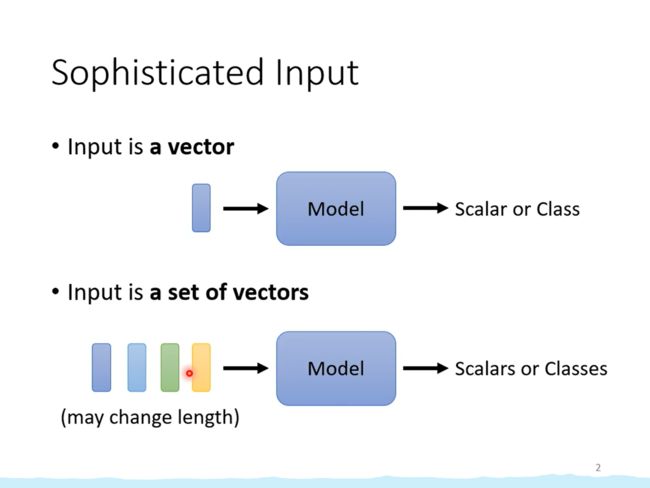
输入是一组向量的例子

假如输入是一个句子，每个单词是一个向量，由于句子的长度不固定，所以这组向量的长度也不确定。

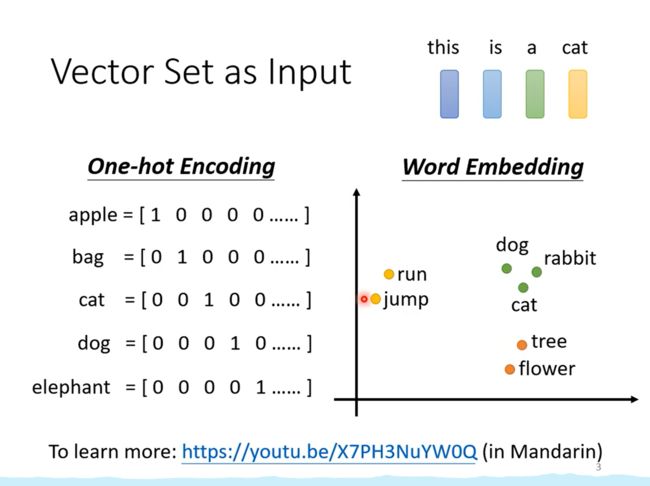
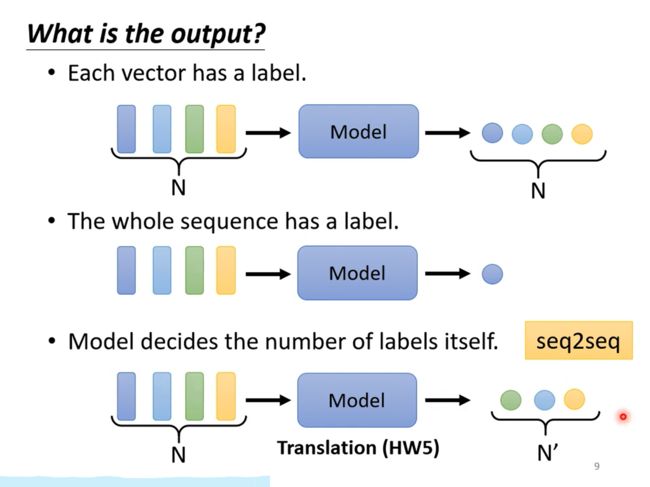
输入是一组向量时输出的可能

输入是一组N个向量时输出的可能有三种

1. 输出是N个label
2. 输出是一个label
3. 输出是N‘个向量
   

自注意力机制核心思想

Self-attention的输入是所有输入向量，输出相同数量的向量，每个向量都考虑了所有输入向量。再经过全连接网络输出。
这样每个全连接网络就不是只考虑一个小的范围，而是考虑了整个句子的信息。

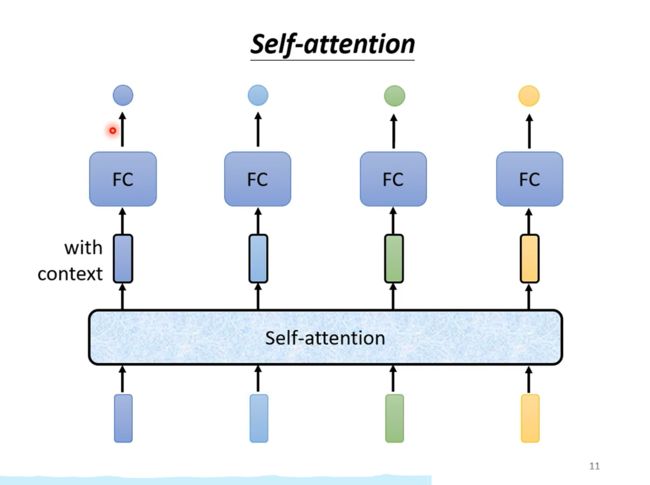
Self-attention不是只能用一次，而是可以叠加。

自注意力机制具体细节

$b^1$是考虑了$a^1,a^2,a^3,a^4$产生的，同理$b^2,b^3,b^4$也是。

以$b^1$为例，讨论$b^1$向量是如何产生的。

第一步，计算$a^1$与其他输入向量的相关性
计算两个向量相关性的具体方式如下

计算$a^1$与其他向量的相关性后，再过一个Soft-max，输出就得到另一排向量。

把$a^1$乘上$W^v$得到新的向量$v^1$，再根据公式
$$b^1=\sum _i{a}_{1,i}^{{}^{\prime }}{v}^i$$
计算得到$b^1$

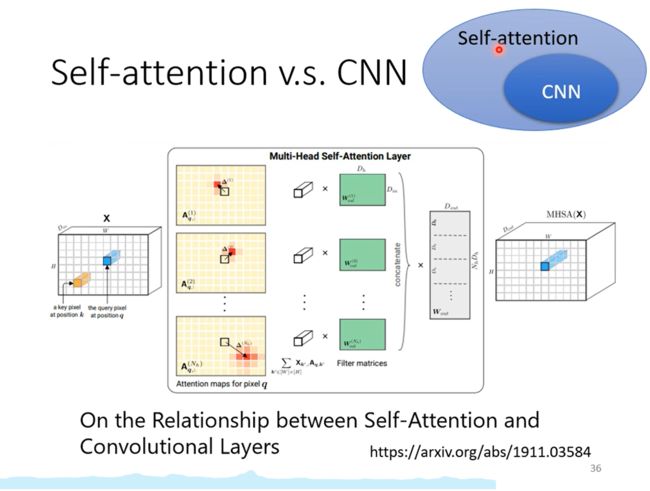
Self-attention和CNN的关系

CNN可以看成是简化版的Self-attention
Self-attention是一个复杂化的CNN
Self-attention中CNN的感受野是自己学出来的

CNN是Self-attention的特例

参考资料

(强推)李宏毅2021/2022春机器学习课程
p26-p39