DW李宏毅机器学习笔记—Task05(五)—批次标准化(Batch Normalization)简介
文章目录
- 前言
- Changing Landscape
- Feature Normalization
-
- FN计算方法
- Considering Deep Learning
- 标准化中间结果
- Testing
- Batch normalization 在CNN中的应用
- BN就是唯一的办法?
- 总结
前言
这是我在Datawhale组队学习李宏毅机器学习的记录,既作为我学习过程中的一些记录,也供同好们一起交流研究,之后还会继续更新相关内容的博客。
Changing Landscape
我们在解决问题时,一种的方向是不断改进我们的方法,第二种方向就是不断简化问题。同理,我们在训练时,不仅可以改进我们的训练方法,也可以对我们的Error Surface进行简化,变得简单易于训练。

上图中蓝色图像的成因就是 x i x_i xi的取值范围相差较大而造成的,这种椭圆状Surface实际也更难训练,所以我们想将Surface简化为右侧绿色图像,就是要把 x i x_i xi的范围设定得相同。
Feature Normalization
FN计算方法
我们现在的问题就是如何让 x i x_i xi的范围设定得相同。
这里用到的方法统称为Feature Normalization。
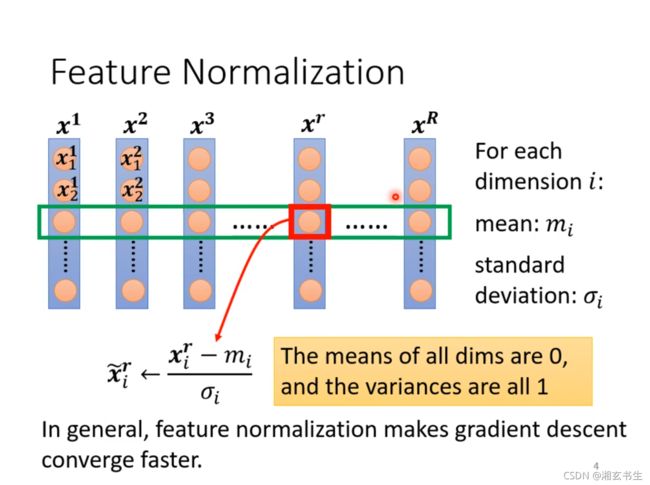
首先先对上图中的参数进行一些说明:
dimension :维度;
m i m_i mi:不同特征组的同一个维度中的元素的平均值;
σ i \sigma_i σi:不同特征组的同一个维度中的元素的标准差;
然后用公式求出 x i r ~ \tilde{x_i^r} xir~代替 x i r {x_i^r} xir,这样就叫做标准化。
这可以使同一纬度上的值的平均数为0,方差为1。这样可以使dimension都在0上下,来制造出一个比较好的Error Surface,最终让Loss收敛得更快一些。
Considering Deep Learning
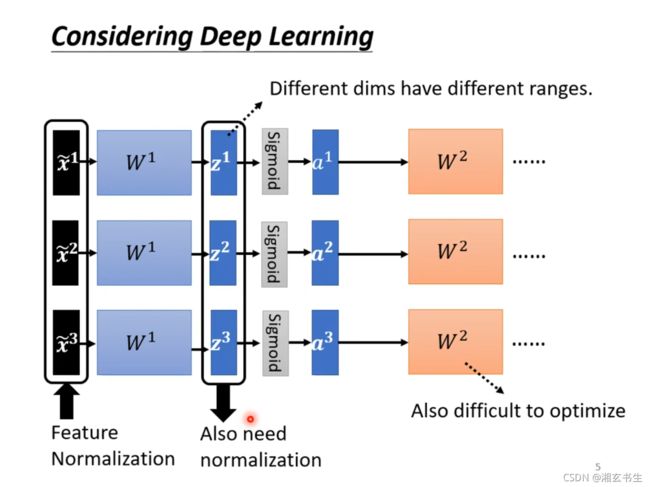
在DL中网络有多层,上一层的输出就是下一层的输入。在最开始input时对 x i x_i xi进行了处理,但在多层神经网络中,那些中间值是没有进行处理的。
为了获得一个简单的Surface,我们要对每一层的输入进行之前的处理。
而我们发现在两层网络之间有一个激活函数sigmoid,那是在sigmoid之前处理好一点呢,还是之后处理好一点呢?
其实这差距不大,但由于Sigmoid函数在0附近斜率比较大,先处理会让sigmoid的输入在0附近,可以使输出更有差异,所以对于Sigmoid激活,我们一般在上一层输出时就进行处理。但对于其他激活函数,也许在激活后处理效果更好,这就需要我们去实验观察效果了。
标准化中间结果

上图中是对中间结果进行处理, μ 和 σ \mu和 \sigma μ和σ的计算方式就如上图所示。
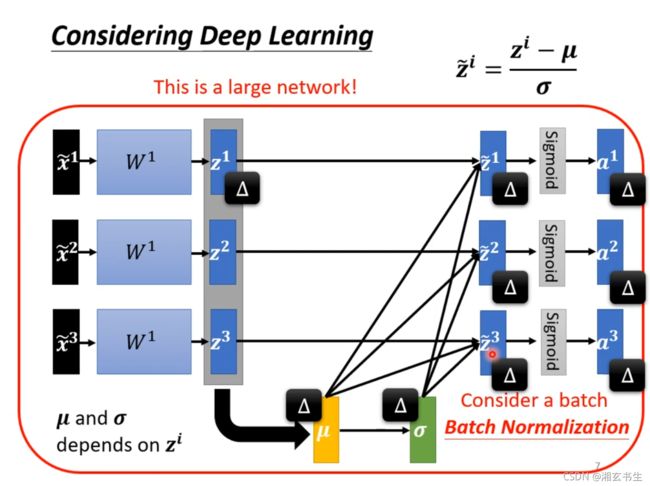
再通过右上角的计算式计算后。将 z i 替 换 为 z i ~ {z^i}替换为\tilde{z^i} zi替换为zi~。注意,计算式中各个变量都是向量,而做的这些运算就都是对于向量中对应元素的运算。
注意,在神经网络的中间值标准化时,每个 z i {z^i} zi的变化会影响 μ 和 σ \mu和 \sigma μ和σ还有其他所有 z i ~ 和 a i \tilde{z^i}和{a^i} zi~和ai的值。
说到这里,我们会发现在神经网络训练时的中间结果会特别多,很容易就爆显存。所以我们要考虑分批次训练。批次和标准化结合就是我们这篇博文的标题《批次标准化》。
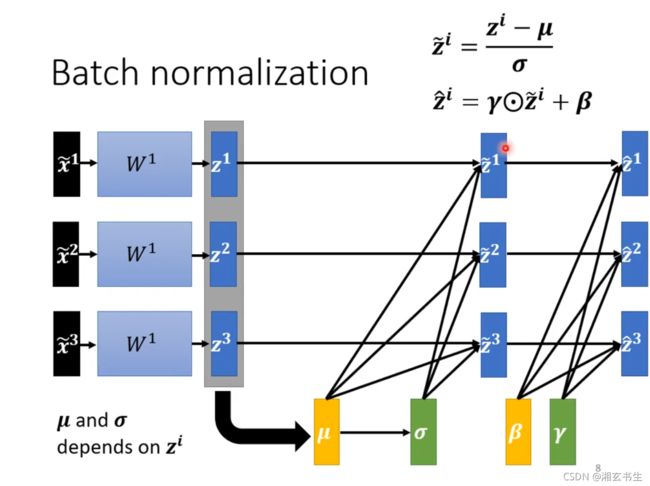
在求得 z i ~ \tilde{z^i} zi~后有时会有这个操作:将 z i ~ 和 γ \tilde{z^i}和\gamma zi~和γ中的元素两两相乘再加上 β \beta β。而 β 和 γ \beta和\gamma β和γ是神经网络单独训练出来的。
而为什么要这么做呢?因为 z i ~ \tilde{z^i} zi~平均数为0,会给神经网络带来一些负面的限制。如果不想平均是0,就去learn β 和 γ \beta和\gamma β和γ,然后将 z i ~ \tilde{z^i} zi~转换成 z i ^ \hat{z^i} zi^。
但我们之前标准化后将参数范围都改到相同区间,而进行这样的操作,会不会破坏标准化呢?
的确,这种情况也是可能的。但在实际训练中, β 和 γ \beta和\gamma β和γ最开始都是ones_vector和zeros_vector,对标准化是没有什么影响的,只有在后期快接近终点时, β 和 γ \beta和\gamma β和γ才会表现出差异性,对训练结果稍微有些影响。
Testing
在实际应用场景中,我们可能不会一下得到所有Data,而是用户一点一点的上传的。这个时候,我们不能等待所有Data都上传完毕(Data可能有几十个GB)后再对Data分批次。那我们该怎么办呢?

接下来就是改进我们计算 μ 和 σ \mu和 \sigma μ和σ的方法。把一次上传的数据分成一个批次, μ t \mu^t μt代表的是第t个batch的平均值。 σ i \sigma^i σi代表每个批次的标准差。 μ ˉ 和 σ ˉ \bar{\mu}和\bar \sigma μˉ和σˉ分别代表之前Batch的加权平均值和加权标准差。而权重P是自己设定的。通过上图下方的式子算出 μ ˉ 和 σ ˉ \bar{\mu}和\bar \sigma μˉ和σˉ。每读入一个batch,就求出 μ i 和 σ i \mu^i和\sigma^i μi和σi并更新 μ ˉ 和 σ ˉ \bar{\mu}和\bar \sigma μˉ和σˉ从而得到 z ~ \tilde{z} z~。
Batch normalization 在CNN中的应用
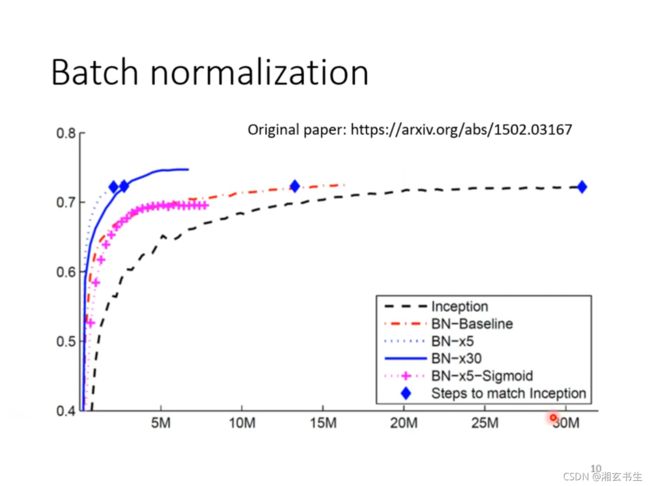
上图中的链接就是相关的论文。上图的图像是使用BN和未使用BN等情况下,训练时间的曲线图。图中菱形表示训练终点,这表示是否使用BN都不会影响训练终点,但相较之下。未使用BN的黑色曲线达到终点的时间是使用BN的橙色曲线的两倍。而且即使是使用了较复杂的Sigmoid函数,在使用BN后也比未使用BN的函数用时更短。
此外,当使用BN时,Error Surface会比较简单,所以Learning Rate可以调得更大,图中 ∗ 5 、 ∗ 30 *5、*30 ∗5、∗30就是Learning Rate放大5、30倍。
BN就是唯一的办法?
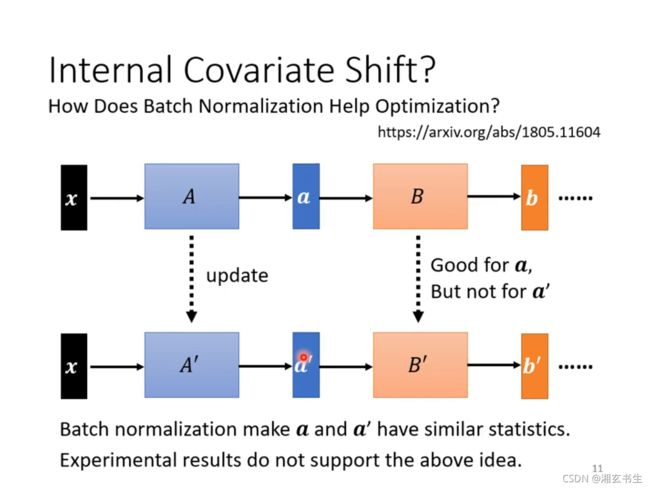

通过理论论证和实验验证发现,BN在最优化中的确有较好的效果。但BN就是唯一能做到这个的吗?显然不是,BN就像偶然发现的青霉素一样,虽然发现时比较偶然,但效果好。而之后也有很多青霉素的代替品出现。
总结
这节主要介绍了BN,从其出现原因到计算方法,以及细节上的处理和应用,简而不略。
