吴恩达机器学习笔记-无监督学习
机器学习-无监督学习
- 一、什么是无监督学习
- 二、聚类算法(无监督学习)
-
- 1、聚类算法的应用
- 2、K-Means算法
-
- 算法流程--图例
- 算法流程--文字描述
- K-means分离不佳簇问题
- K-means代价函数
- K-means的随机初始化
- 如何选取聚类数量K
- 代码实例(鸢尾花)
- 三、PCA降维
-
- 1. 什么是降维
- 2. 主成分分析方法(principal components analysis，PCA)
-
- 文字方式描述PCA
- PCA过程(n维数据降到k维)
- 3. 压缩重现
- 4. 选择K值
- 5. 应用PCA的建议
- 6. 代码实例(鸢尾花)
- 四、异常检测
-
- 1. 问题动机
- 2. 异常检测应用
- 3. 高斯分布中的参数估计问题
- 4. 异常检测算法
- 5. 评估异常检测算法
- 6.异常检测VS监督学习
- 7. 选择特征features
- 8. 多元高斯分布
- 9. 使用多元分布的异常检测
- 10. 代码实例
- 五、推荐系统
-
- 1. 问题描述
- 2. 基于内容的推荐算法
- 3. 协同过滤
- 4. 协同过滤算法
- 5. 向量化：低秩矩阵分解
- 6. 实施细节
- 7.代码实例
- 六、大规模机器学习
-
- 1. 学习大数据集
- 2. 随机梯度下降
- 3. Mini-batch梯度下降
- 4.随机梯度下降收敛
- 5. 在线学习
- 6.减少映射与数据并行
- 七、应用示例：Photo OCR
-
- 1.问题描述与.OCR.pipeline
- 2.滑动窗口分类器
- 3.获取大量数据和人工数据
- 4.上限分析
一、什么是无监督学习
无监督学习与监督学习的对比：
（1）无监督学习
我们有一组带标签的Training Set，希望通过训练得到一条拟合Training Set的决策边界。
【即有一系列标签，然后假设函数去拟合它】
（2）无监督学习
Training Set不带标签y，无监督学习的任务就是将这些无标签的数据输入算法中，找到一些隐含在数据中的结构。
【例如：聚类算法】
二、聚类算法(无监督学习)
1、聚类算法的应用
（1）市场分割
将客户分成不同人群，针对性产品销售
（2）社会关系网划分
在社交网络中找到关系密切的朋友
2、K-Means算法
算法流程–图例
-
存在一些无标签的数据
目标是将上列数据分成两簇 -
先假定两个
聚类中心点
-
根据距离对数据点进行划分(染色)
-
重新确定
新的聚类重心点(两类样本的均值)
-
由新的聚类中心重新划分样本
-
重复5、6(进行迭代)，直到
聚类中心不发生改变
算法流程–文字描述
- K-means的
Input：
(1)K：聚类的个数
(2)Training Set：{x(1),x(2),…,x(m)}
- m表示训练集数据的个数
- x(i)是n维的，即训练集样本由n个特征feature
- 随机
初始化K个聚类中心u1、u2、…、uk
然后重复以下步骤：
（1）对第1~m个样本，计算到K各聚类中心的距离||x(i)-u k||，将其划分(染色)给最接近该样本点的聚类中心【划分训练集各样本点】
（2）对于第1~K个聚类中心，u k=第k类样本的均值【移动聚类中心】
扩展：
若存在某个聚类中心并没有分类到样本点：
（1）删去该聚类中心–>K-1个分类【通常做法】
（2）重新随机初始化这个聚类中心
K-means分离不佳簇问题
假设存在某一家服装厂，记录了客户的身高和体重；想要设计小、中、大三种尺寸的服装，该如何设计？
可以使用K-means将上图数据分成三类，再针对性的对各类样本进行尺寸设计。
K-means代价函数
c(i) ：第i个样本所属的簇的索引或序号
uk ：第k个聚类中心的位置
uc(i) ：第i个样本所属簇的聚类中心的位置
K-means的优化目标函数：
J(c,u)表示各样本点到样本所属簇聚类中心的距离，minJ(c,u)是希望各样本点到所属簇聚类中心距离达到最小
K-means算法过程就是在最小化目标函数J(c,u)
K-means的随机初始化
- 应该确保K
- 随机选取K个训练集样本
- 将k个聚类中心赋值为这K个训练集样本
对于不同的初始化，可能收敛到
不同的局部最优
例如下图，你可能会收敛到三种不同的分类结果
为了避免K-means落到局部最优，应该进行多次随机初始化。
例如上图，进行了100次随机初始化，得到了很多种分类结果；接下来要做的就是在很多分类结果中选取代价函数最小的一个。
当K较小时，多次随机初始化优化效果会很好；
当K较大时，多次随机初始化效果不会很明显。
如何选取聚类数量K
如下图，同一份数据可以划分成2类或者4类，这两种分类都可以说是正确的。因为这是无监督学习，因此不存在所谓的绝对正确答案。
在讨论K的选择时，一般会讨论到一个方法，叫作肘部法则
不断改变的K，画出代价函数J，根据图像选取合适的K。
如上图，在K=3时，代价函数下降缓慢，因此我们可以选择K=3。
但在实际应用中，代价函数图像并没有上述的那么"友好"，如下图：
你不知道该选择3还是4，或者是5；因此肘部法制在这里并不能很好的确定K的值。
此外，你可以通过分类的后续目的去考虑K值。例如，某厂家要根据客户身高、体重来设计不同大小的尺寸。
当K=3，可把尺寸设计为S、M和L；当K=5，可把尺寸设计为XS、S、M、L、XL。
此时可以通过背后的经济价值去考虑K=3还是5。
代码实例(鸢尾花)
1、读入数据集
import pandas as pd#读入csv文件
import numpy as np#处理数据
import random #随机初始化需要使用
#导入数据集
iris = pd.read_csv("iris.csv",header=None)
iris.head(10)
数据头十行如下图所示
为了可视化，只考虑前两个特征
#读取鸢尾花的前两个特征
feature = iris.iloc[:,0:2]
#转换成数组
feature = np.array(feature)
2、随机初始化，获得K个聚类中心
'''
dataset:数据集
K:聚类中心个数
'''
def create_centrois(dataset,K):
data = dataset[random.sample(range(0,len(dataset)),K)]
return data
random.sample(range(0,len(dataset)),K)：
随机产生K个数，范围从0到len(dataset)。代表选取数据集中的下标
3、计算欧式距离
def get_distance(dataset,centrois):
K = len(centrois)#聚类数
m = len(dataset)#样本个数
#计算各样本到K个聚类中心的聚类：m*K大小的二维数组，先初始化为0
distance = np.zeros((m,K))
#进行K轮循环，计算各样本点到第k个聚类中心的距离
for k in range(K):
#获取第k个聚类中心坐标
center = centrois[k]
#计算欧式距离
#tile(a,(x,y))-->将a沿x轴扩大x倍，y轴扩大y倍
#(tile作用就是将聚类中心坐标扩变的和数据集一样大，以进行逐位相减)
dis = np.tile(center,(m,1))-dataset
#平方
sqrDis = dis**2
#按行相加
sqrDisSum = sqrDis.sum(axis=1)
#赋值到distance的第k列
distance[:,k]=sqrDisSum
return distance
4、绘图函数
from matplotlib import pyplot as plt
'''
dataset：数据集
lab：分类结果(标签)
centers：K个聚类中心的坐标数组
dic_colors：设置颜色
'''
def draw_kmeans(dataset,lab,centers,dic_colors=None):
#清除画布
plt.cla()
#转换成一维数组
lab = lab.flatten()
#将标签转换成列表在通过集合去重
#val_labs表示目前有几类别，每个类别的标签
val_labs = set(lab.tolist())
#遍历集合val_labs
for i,val in enumerate(val_labs):
#获取标签位val的样本下标
index = np.where(lab==val)
#将这一类样本的坐标都存到一个数组里面
sub_dataset = dataset[index]
#散点图绘制(这里只有两个特征)
plt.scatter(sub_dataset[:,0],sub_dataset[:,1],s=14,color = dic_colors[i])
#绘制聚类样本中心
for i in range(np.shape(centers)[0]):
plt.scatter(centers[i,0],centers[i,1],s=200,color = "k",marker="+")
plt.show()
5、K-means函数
'''
dataset:数据集
K：聚类个数
iter:最大迭代次数(最多移动聚类中心次数)
draw:是否绘图
'''
def K_means(dataset,K,iter=20,dic_colors=None,draw=False):
#m：样本个数；n:样本维度
m,n = np.shape(dataset)
#随机初始化聚类中心
centrois = create_centrois(dataset,K)
#类别标签初始化位0，表示都属于一类
lab = np.zeros(m)
if draw:
#画出未分类时的数据图像
draw_kmeans(dataset,lab,centrois,dic_colors)
#迭代iter次，每次更新一次聚类中心
for i in range(iter):
#获得欧式距离
distance = get_distance(dataset,centrois)
#划分样本
#argmin返回最小值所在的序号(列)，axis=1按行比较
#最小距离所在的序号即当前所属标签
lab_new = np.argmin(distance,axis=1)
#目标函数值
cost = np.sum(np.min(distance,axis=1))/m
print("第%d次聚类目标函数值为%.2f"%(i,cost))
if draw:
#第i次聚类结果
draw_kmeans(dataset,lab,centrois,dic_colors)
#计算新的聚类中心
for k in range(K):
index = np.where(lab_new==k)[0]
#取均值
centrois[k,:] = np.mean(dataset[index,:],axis=0)
if draw:
#新值作为聚类中心，进行绘图
draw_kmeans(dataset,lab,centrois,dic_colors)
#聚类中心不变，则退出
if np.sum(lab_new-lab) == 0:
return lab_new
else:
#聚类中心移动，进入下一次迭代
lab = lab_new
#返回分类结果
return lab
6、调用
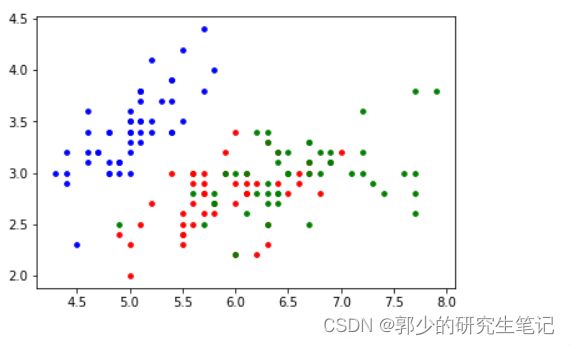
K_means(feature,3,20,['red','green','blue'],False)
聚类结果：
真实的聚类结果：
7、完整代码
import pandas as pd#读入csv文件
import numpy as np#处理数据
import random #随机初始化需要使用
#导入数据集
iris = pd.read_csv("iris.csv",header=None)
iris.head(10)
#读取鸢尾花的前两个特征
feature = iris.iloc[:,0:2]
#转换成数组
feature = np.array(feature)
'''
dataset:数据集
K:聚类中心个数
'''
def create_centrois(dataset,K):
data = dataset[random.sample(range(0,len(dataset)),K)]
return data
def get_distance(dataset,centrois):
K = len(centrois)#聚类数
m = len(dataset)#样本个数
#计算各样本到K个聚类中心的聚类：m*K大小的二维数组，先初始化为0
distance = np.zeros((m,K))
#进行K轮循环，计算各样本点到第k个聚类中心的距离
for k in range(K):
#获取第k个聚类中心坐标
center = centrois[k]
#计算欧式距离
#tile(a,(x,y))-->将a沿x轴扩大x倍，y轴扩大y倍
#(tile作用就是将聚类中心坐标扩变的和数据集一样大，以进行逐位相减)
dis = np.tile(center,(m,1))-dataset
#平方
sqrDis = dis**2
#按行相加
sqrDisSum = sqrDis.sum(axis=1)
#赋值到distance的第k列
distance[:,k]=sqrDisSum
return distance
from matplotlib import pyplot as plt
'''
dataset：数据集
lab：分类结果(标签)
centers：K个聚类中心的坐标数组
dic_colors：设置颜色
'''
def draw_kmeans(dataset,lab,centers,dic_colors=None):
#清除画布
plt.cla()
#转换成一维数组
lab = lab.flatten()
#将标签转换成列表在通过集合去重
#val_labs表示目前有几类别，每个类别的标签
val_labs = set(lab.tolist())
#遍历集合val_labs
for i,val in enumerate(val_labs):
#获取标签位val的样本下标
index = np.where(lab==val)
#将这一类样本的坐标都存到一个数组里面
sub_dataset = dataset[index]
#散点图绘制(这里只有两个特征)
plt.scatter(sub_dataset[:,0],sub_dataset[:,1],s=14,color = dic_colors[i])
#绘制聚类样本中心
for i in range(np.shape(centers)[0]):
plt.scatter(centers[i,0],centers[i,1],s=200,color = "k",marker="+")
plt.show()
'''
dataset:数据集
K：聚类个数
iter:最大迭代次数(最多移动聚类中心次数)
draw:是否绘图
'''
def K_means(dataset,K,iter=20,dic_colors=None,draw=False):
#m：样本个数；n:样本维度
m,n = np.shape(dataset)
#随机初始化聚类中心
centrois = create_centrois(dataset,K)
#类别标签初始化位0，表示都属于一类
lab = np.zeros(m)
if draw:
#画出未分类时的数据图像
draw_kmeans(dataset,lab,centrois,dic_colors)
#迭代iter次，每次更新一次聚类中心
for i in range(iter):
#获得欧式距离
distance = get_distance(dataset,centrois)
#划分样本
#argmin返回最小值所在的序号(列)，axis=1按行比较
#最小距离所在的序号即当前所属标签
lab_new = np.argmin(distance,axis=1)
#目标函数值
cost = np.sum(np.min(distance,axis=1))/m
print("第%d次聚类目标函数值为%.2f"%(i,cost))
if draw:
#第i次聚类结果
draw_kmeans(dataset,lab,centrois,dic_colors)
#计算新的聚类中心
for k in range(K):
index = np.where(lab_new==k)[0]
#取均值
centrois[k,:] = np.mean(dataset[index,:],axis=0)
if draw:
#新值作为聚类中心，进行绘图
draw_kmeans(dataset,lab,centrois,dic_colors)
#聚类中心不变，则退出
if np.sum(lab_new-lab) == 0:
return lab_new
else:
#聚类中心移动，进入下一次迭代
lab = lab_new
#返回分类结果
return lab
if __name__=="__main__":
K_means(feature,3,20,['red','green','blue'],False)
三、PCA降维
1. 什么是降维
例如存在两个特征x1，x2，x1表示该对象的英寸长度，x2表示该对象的厘米长度。
我们可以通过降维，将二维数据降成一维数据。只通过一个特征来表示对象的长度
降维意味着什么呢？
现在对于第i个样本x(i)，可以需要二维的数据才能表示。降维后意味着仅需要一维数据z(i)就可以表示x(i)，如下图。【x(i)→z(i)】
降维后，只需要一个值就可以指定在二维图中直线上的位置。
三维降成二维的例子：
图中的三维数据大致都处于一个平面，因此可以将此投影在一个二维平面上，从而降为二维的数据。
【三维投影到面，二维投影到线】
2. 主成分分析方法(principal components analysis，PCA)
对于二维的数据降维，其实就是找到一条一维的投影(线)；各样本到该投影的距离最小。
所以，PCA做的就是找一条低纬平面，然后将数据投影在上面，使各样本到该投影的长度平方(投影误差)最小
文字方式描述PCA
对于2维到1维:我们需要找到一个向量u(1)【u(1)是正是负都可以，即方向不重要，投影误差最小即可】
对于高纬的数据：
从n维降到k维：找到k个向量:u(1),u(2),…,u(k)；我们要将数据投影到这k个向量展开的线性子空间上。
PCA与线性回归
(1)他们想缩小的误差，在方向上不同。线性回归是缩小在x轴投影上的误差；PCA是缩小到投影线的误差。
(2)线性回归有特殊的值y，而PCA钟的变量都是平等对待的。
PCA过程(n维数据降到k维)
1、 在使用PCA之前需要对数据进行预处理，与监督学习的特征缩放相同。
（1）对于每个feature，减去其对应的均值【期望变成0】
(2)若各feature取值范围跨度差距大，除于max-min或者标准差
2、计算协方差矩阵(covariance matrix)
∑是一个n*n的矩阵
（1）前面的∑表示希腊字母σ的大写，表示协方差；后面的是求和符号。两者不相同
（2）特征缩放后期望为0，所以协方差就是两个输入的内积
3、 计算协方差矩阵(Sigma)的特征向量。
下图是octave代码
S对应的是奇异值分解中的奇异值矩阵，奇异值类似方阵中的特征值，是表示特征值向量重要程度的一个东西。S中的矩阵是按照奇异值递减排序的，所以取前k个就能得到最重要的k个向量。这k个向量作为我们降维后要用的特征向量，这k个特征向量蕴含了原来的特征的绝大部分，所以用他们来代替而不损伤太多信息。
4、奇异值分解后，从特征向量中选取前K个特征向量；得到一个n*k的矩阵，称为为U_reduce矩阵
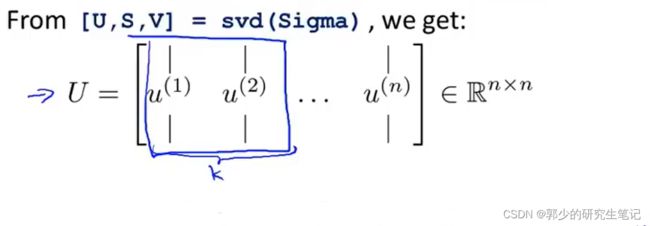
5、降维
将U_reduce转置乘于输入x(i)，得到一个k*1矩阵，从而实现降维。
3. 压缩重现
在PCA中我们将n维的输入x降到了k维的z，那能否通过k维的z返回到原来的n维x呢？
降维过程如下图所示：
U是酉矩阵，即UUT=1，上图式子右边同时乘于U得到：x_approx =U_reduce*z
关于什么是x_approx：
（1）首先z是x投影到k维平面上的坐标。例如三维降到二维，z是在二维平面上的坐标
（2）我们逆向从z推导x，逆推的是x在n维空间中的z维平面上的坐标，这个坐标就是x_approx举个实例:x_approx就是下图图(b)坐标，而不是逆推到图(a)中的坐标
4. 选择K值
Average squared projection erro:投影后的平均均方误差。这个误差可以看作投影过后与原数据的差异程度，误差过大则原数据之间的关系信息很多都丢失了。所以我们希望Average squared projection erro越小越好
Total variation in data:训练集的总方差,也可以看作与原点之间的距离。
选择K值时希望能够满足下面的条件：
也可以不选择0.01，当我们讨论选择k时，不是直接选择k，而是要选择0.01这个数字或者其他数字。
这里选择了0.01，用术语说是保留了99%的方差特性。或者用另一种PCA的说法是99%的差异值被保留下来了。
大于等于85%的值都是比较典型的，95%-99%是比较常用的。
选择实现过程
从k=1开始计算这个数值，若不等式不成立则让k=2，k=3……，假设到k=17时满足了不等式则用17作为k值。
但是这种选择算法效率并不高，好在奇异值分解svd可以让这个事好算很多
SVD会返回三个值，其中S是一个对角矩阵，对于给定的k，我们可以将不等式左部进行替换，如下图：
从而验证下图式子即可:
选择满足不等式的最小k值即可
这样就可以只调用一次svd函数得到S矩阵，迭代计算S矩阵中的数值
5. 应用PCA的建议
通常运用PCA对监督学习算法进行加速。
例如下图，在监督学习原始训练集数据中，输入x是10000维的数据，数量级很大训练过程会很复杂；可以通过PCA降维成1000维的数据集，降低了训练的复杂性。
PCA做的是寻找x到z的映射，对于测试集中的样本，也应该经过PCA降维后再输入到假设模型中。
PCA的应用：
（1）能进行压缩，减少存储空间
（2）加快算法速度
（3）可视化数据
PCA的错误用法：去防止过拟合：
推荐使用正则化来防止过拟合
在使用PCA前应该先考虑完整的原始数据是否能满足你的需要；当内存不够或训练速度过慢才应该考虑PCA。
6. 代码实例(鸢尾花)
1、数据中心化，对于每个feature，减去其对应的均值
def PCA(dataset,k):
#获取数据的样本数m和维度n
m,n = np.shape(dataset)
#数据预处理，各数值减去均值；若数据取值范围差距大，除于标准差或max-min
dataset = dataset - np.mean(dataset,axis=0)
#计算协方差矩阵
covariance_matrix = np.dot(dataset.T,dataset)/m
#计算协方差矩阵特征向量(svd分解)
u,s,v = np.linalg.svd(covariance_matrix)
#取u的前几列作为U_reduce矩阵
U_reduce = u[:,:k]
#U_reduce乘输入数据完成降维
z = np.dot(dataset,U_reduce)
#返回降维后的z和矩阵U_reduce
return z,U_reduce
2、绘图函数
from matplotlib import pyplot as plt
'''
dataset：数据集
lab：分类结果(标签)
dic_colors：设置颜色
'''
def draw_pic(dataset,lab,dic_colors=None):
#清除画布
plt.cla()
#转换成一维数组
lab = lab.flatten()
#将标签转换成列表在通过集合去重
#val_labs表示目前有几类别，每个类别的标签
val_labs = set(lab.tolist())
#遍历集合val_labs
p = []
legends = []
for i,val in enumerate(val_labs):
#获取标签位val的样本下标
index = np.where(lab==val)
#将这一类样本的坐标都存到一个数组里面
sub_dataset = dataset[index]
#散点图绘制(这里只有两个特征)
pi = plt.scatter(sub_dataset[:,0],sub_dataset[:,1],s=14,color = dic_colors[i])
p.append(pi)
legends.append(val)
plt.legend(p,legends)
plt.show()
3、调用
if __name__ == "__main__":
#导入数据集
iris = pd.read_csv("iris.csv",header=None)
#读取鸢尾花的四个特征
feature = iris.iloc[:,0:4]
#转换成数组
feature = np.array(feature)
#获取鸢尾花分类(标签)
lab = iris.iloc[:,4:5]
lab = np.array(lab)
#对数据从4维降到2维，便于可视化
z,U_reduce = PCA(feature,2)
#可视化
draw_pic(z,lab,['green','blue','yellow'])
结果输出
4、完整代码
import numpy as np
import pandas as pd
def PCA(dataset,k):
#获取数据的样本数m和维度n
m,n = np.shape(dataset)
#数据预处理，各数值减去均值；若数据取值范围差距大，除于标准差或max-min
dataset = dataset - np.mean(dataset,axis=0)
#计算协方差矩阵
covariance_matrix = np.dot(dataset.T,dataset)/m
#计算协方差矩阵特征向量(svd分解)
u,s,v = np.linalg.svd(covariance_matrix)
#取u的前几列作为U_reduce矩阵
U_reduce = u[:,:k]
#U_reduce乘输入数据完成降维
z = np.dot(dataset,U_reduce)
#返回降维后的z和矩阵U_reduce
return z,U_reduce
from matplotlib import pyplot as plt
'''
dataset：数据集
lab：分类结果(标签)
dic_colors：设置颜色
'''
def draw_pic(dataset,lab,dic_colors=None):
#清除画布
plt.cla()
#转换成一维数组
lab = lab.flatten()
#将标签转换成列表在通过集合去重
#val_labs表示目前有几类别，每个类别的标签
val_labs = set(lab.tolist())
#遍历集合val_labs
p = []
legends = []
for i,val in enumerate(val_labs):
#获取标签位val的样本下标
index = np.where(lab==val)
#将这一类样本的坐标都存到一个数组里面
sub_dataset = dataset[index]
#散点图绘制(这里只有两个特征)
pi = plt.scatter(sub_dataset[:,0],sub_dataset[:,1],s=14,color = dic_colors[i])
p.append(pi)
legends.append(val)
plt.legend(p,legends)
plt.show()
if __name__ == "__main__":
#导入数据集
iris = pd.read_csv("iris.csv",header=None)
#读取鸢尾花的四个特征
feature = iris.iloc[:,0:4]
#转换成数组
feature = np.array(feature)
#获取鸢尾花分类(标签)
lab = iris.iloc[:,4:5]
lab = np.array(lab)
#对数据从4维降到2维，便于可视化
z,U_reduce = PCA(feature,2)
#可视化
draw_pic(z,lab,['green','blue','yellow'])
四、异常检测
1. 问题动机
假设你是飞机引擎检察员，每次飞机起飞都会从引擎上收集数据，如x1、x2；一段时间的检查后获得了数据集Dataset。
当有一个新的引擎在流水线上被生产出来，这个新引擎有一个特征变量集xtest。所谓的异常检测问题就是：希望知道这个新的飞机引擎是否有某种异常
异常检测：
存在一个数据集合Dataset，这个数据集中的样本全是合格的或全是不合格的；然后需要一个算法来预测新样本xtest是否合格。
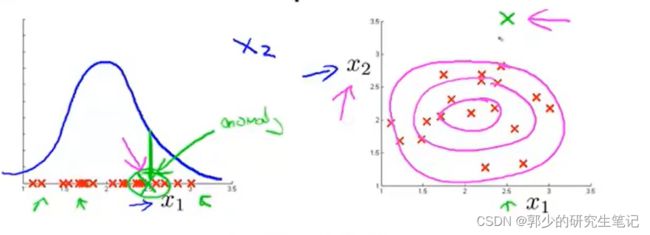
要做的是训练一个模型，找到一个概率分布函数p(x)；当p(x)小于某个阈值，则该样本是不合格的；大于等于某个阈值，该样本是合格的。
如上图，假设我们找到了一个概率分布，越靠近中心，p(x越大)，合格的概率就越大。
2. 异常检测应用
（1）欺诈检测：
假设你有很多的客户在从事不同活动，可以对不同的用户活动计算特征变量x(i)，于是你可以建立一个模型来表示用户表现出各种行为的可能性；从而检测用户的异常行为或欺诈行为。
（2）工厂
例如飞机引擎的异常检测
（3）数据中心的计算机监控
3. 高斯分布中的参数估计问题
假设有一个数据集Dataset，已经知道该数据集遵从高斯分布；参数估计问题即确定u和σ，从而确定一个高斯分布函数。
u的预估公式：
对所有样本求均值
σ的预估公式：
对所有样本求方差
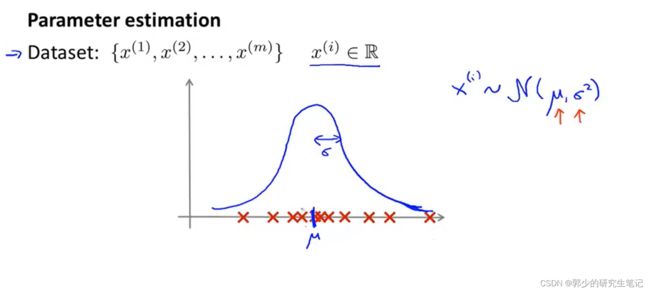
在数学领域通常除的是(m-1)，但在机器学习实践中通常除的是m，在实际应用中m和(m-1)之间的差异不大
4. 异常检测算法
1、 选择认为会对异常检测造成影响的特征xi
2、计算参数u1、u2、……、un、σ21、σ22……、σ2n(假设各特征遵从高斯分布)
3、对给的的新样例，计算p(x)；小于阈值则有异常
这里的p(x)为：
虽然各特征之间不一样严格相互独立，但可以得到比较好的预测效果
异常检测例子：
上图中有两个特征x1和x2，分别对应两个概率密度函数p1和p2；p(x)=p1*p2，左下角为p(x)的图像。我们可以假设阈值 ε=0.02，对于新样本带入p(x)判断与 ε的大小关系即可。
对于p(x)函数图，越接近中心(红色)的部分值越大，即非异常；越靠近边缘的蓝色部分值越小，即异常。
5. 评估异常检测算法
假设拥有一些带有标签的数据集，包含异常和非异常两种样本。(y = 0为非异常；y = 1为异常)
将数据集分成训练集(只包含异常或非异常的无标签样本)、验证集(包含异常和非异常的带标签样本)、测试集(包含异常和非异常的带标签样本)
以飞机引擎异常检测为例子：
拥有一个包含10000个非异常样本和20个异常样本的带标签数据集。
可以将数据集以60%、20%、20%的比例分成训练集、验证集、测试集。异常样本，测试集和训练集平分。
(1)训练集看作无标签样本，只包含非异常样本，训练出模型p(x)；
(2)验证集是有标签样本，用训练出来的p(x)对验证集中的样本进行预测。
因为异常值比较少，所以通过True positive、false positive、F1-score等指标去评估模型、选取阈值ε。
【验证集评价模型的同时选取ε】
6.异常检测VS监督学习
| 使用异常检测 | 使用监督学习 |
|---|---|
| y=1的异常样本非常少(0-20),y=0的非异常样本非常多 | y=0的非异常样本和y=1的异常样本都非常多 |
| 导致异常的原因有很多，监督学习很难从少数异常样本中学习到所有能导致异常的原因；对于新样本，监督学习学习到的异常原因不能适用于新样本上 | 有足够的样本去学习异常样本的发生原因；学习过的原因可以很好的使用在新样本上 |
7. 选择特征features
因为上述的异常检测是假设了各feature符合高斯分布；因此我们更倾向于数据特征遵从高斯分布。
在实际应用时，我们可以先画出数据的直方图。
如下图所示，数据分布相对遵从高斯分布，因此很乐意去使用异常检测。
若数据如下图左侧图像所示，分布较为均匀；我们可以通过取对数使其相对遵从高斯分布。
除了取对数外，我们还可以
（1）x1⬅log(xi+c) 【常数c】
（2）x2⬅(x2)1/c 【开根号】
对错误的预测进行异常分析：
一开始使用全部的feature来训练模型，当某一个异常样本被错误预判了，应该对该样本进行讨论，是否存在其他新的特征导致了样本的异常，从而创造一些新的特征将异常样本和非异常样本分隔开。
如下图，左边图像绿色的异常样本混在非异常样本中，仅x1不能将此区分；通过异常分析添加新的特征x2，升维从而将异常样本和非异常样本在更高维空间区分开。
例如：
数据中心的计算机监控，判断电脑工作是否发生异常，目前考虑了以下特征
还存在一种工作异常情况：电脑进入死循环；而上图特征不足以分析到这种异常情况。
所以进入异常分析，当电脑进入死循环情况下，CPU负载变高、网络负载不变，据此我们引入新的特征x5、x6
从而使算法学习到死循环这一个导致电脑工作异常的原因
8. 多元高斯分布
以数据中心的计算机监控为例，在这里考虑了x1和x2两个特征，分布上遵从高斯分布。
现在我们对下图左侧图像中的绿色样本进行异常检测，我们带入到右侧两幅图，可以发现该绿色的p(x)并不低，x1和x2都在正常范围内，因此大概率会被判断为非异常样本；但是观察左侧图像，该样本距离正常样本是有一点距离的，是异常样本的概率很大。因此，上述的异常检测并不能检测到下图左侧图像中的蓝色范围。
导致上述原因是因为x1和x2之间并不相互独立，但异常检测过程中都假设它两遵从不一样的高斯分布，之间相互独立；所以单从某一个特征去看，都在正常范围内，都看不出来异常。
为了避免上述问题，应该使用多元高斯分布：
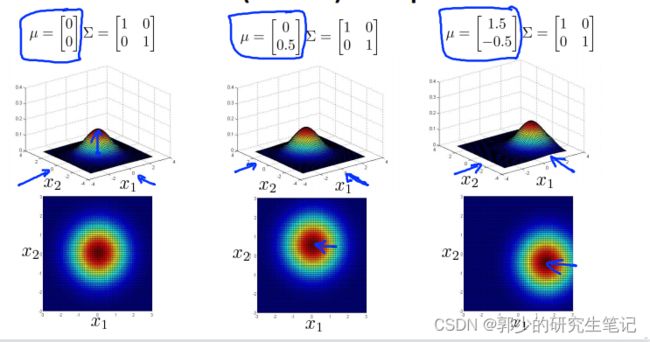
即不使用单独的p(x1)、p(x2)……。模型p(x)使用统一的u(期望)和Σ(协方差矩阵)，即整体样本只遵从一个高斯分布。
u和Σ可以唯一确定一个分布函数，所有我们可以调整u和Σ使多元高斯分布更加拟合数据集。
（1）改变Σ对角线元素
（2）改变Σ斜对角线元素从而改变x1和x2之间的相关性
斜对角线为正，x1和x2正相关
斜对角线为正，x1和x2负相关
（3）改变u从而挪动中心
9. 使用多元分布的异常检测
多元分布的参数估计:
对于所给的训练集数据，若x遵从高斯分布，可以用下图的式子对u和Σ进行估计。
即设u为训练样本的平均值，Σ为训练样本协方差
多元高斯分布函数异常检测流程：
（1）设置u和Σ来拟合模型
（2）对于新的样本，计算p(x_test)
（3）与ε比较判断是否异常
多元高斯分布考虑了各特征之间的相关性，所以上如右侧图像中的蓝色圈是会被学习检测到的。绿色的新样本所在的圈距离高斯分布中心较远，从未p(x)值会很低，从而被判断是异常值。
.
(1)原始的异常检测认为各features之间是相互独立的;多元高斯分布认为各features之间是非相互独立的
(2)原始的异常检测的Σ可以认为是一个对角矩阵
原始异常检测与多元异常检测的选择：
| 原始模型 | 多元高斯 |
|---|---|
| 可以通过分析来添加(组合)新的特征来分析新的异常原因 | 自动捕捉特征之间的相关性，即减少或不用分析 |
| 计算成本低，适合大维度的数据 | 计算成本高，适合维度小的数据 |
| 训练样本数量小时推荐使用 | 必须m>n(m>10n是比较合理的范围)，即训练样本数目大于特征数量时或Σ不可逆时使用 |
多元高斯出现Σ不可逆时原因：
（1）m>n没有满足
（2）存在冗余特征，如x1=x2、x3=x4+x5，导致特征之间线性相关。去掉其中一个冗余特征即可
10. 代码实例
【观看up主:ladykaka007 的视频编写的，感谢up】
题目：
在本练习中，您将实现异常检测算法来检测服务器计算机中的异常行为。这些特性测量每个服务器响应的吞吐量（mb/s）和延迟（ms）。当服务器运行时，您收集了m=307个它们的行为示例，因此有一个未标记的数据集{x(1)，…，x(m)}。您怀疑这些样本中的绝大多数都是服务器正常运行的“正常”（非异常）示例，但也可能有一些服务器在此数据集中异常运行的示例。
您将使用高斯模型来检测数据集中的异常样本。首先从2维的数据集开始，该数据集允许您可视化算法正在执行的操作。在该数据集上，您将拟合高斯分布，然后找到阈值ε，低于该值的将被视作异常。然后，将异常检测算法应用于具有多个维度的较大数据集。
异常检测算法思路：
1、根据训练集数据，计算特征的平均值u和方差Σ
2、根据u和Σ确定一个正态分布p(x)
3、在交叉验证集中使用不同的阈值ε，通过F1-score等指标选择合适的ε
4、选择ε后，对测试集进行预测并计算异常检测系统的F1值
代码：
1、读取.mat数据
import scipy.io as scio
import matplotlib.pyplot as plt
import numpy as np
#导入数据集ex8data1.mat
dataset = scio.loadmat("ex8data1.mat")
#导入的dataset的类型是2、获取训练集和验证集，可视化样本点
'''
dict_keys(['__header__', '__version__', '__globals__', 'X', 'Xval', 'yval'])
__header__:文件信息
__version__：版本信息
X：2维的训练集数据(307，2)
Xval:验证集数据(307，2)
yval：验证集标签(307，1)
'''
#训练集数据
trainData = dataset['X']
#验证集数据和标签
valData,valLabel = dataset['Xval'],dataset['yval']
#训练集样本可视化
plt.scatter(trainData[:,0],trainData[:,1],marker='+',c='c')
当前数据是二维的，训练集样本可视化如下图：
3、根据训练集数据，计算特征的平均值u和方差Σ
#1、获取均值和方差
'''
dataset:传入的数据集
isCovariance：求协方差(多元高斯分布) 还是 各个feature单独求方差(每个特征对应一个高斯分布)
'''
def estimateGaussian(dataset,isCovariance):
#按列求均值
u = np.mean(dataset,axis=0)
#求协方差
if isCovariance:
cov = (dataset-u).T@(dataset-u)/len(dataset)
else:
#按列求方差，即每个特征一个方差
cov = np.var(dataset,axis=0)
return u,cov
4、根据u和Σ确定一个正态分布p(x)
#2、根据u和Σ确定一个正态分布p(x)
def gaussian(dataset,u,cov):
#若传的是一维的协方差，转为对角矩阵
#在原始模型中，假设各feature之间相互独立，所以对应协方差矩阵除了对角线外都是0
if np.ndim(cov)==1:
cov = np.diag(cov)
#计算(x-u).T
x_u = dataset-u
#计算维度n
n = dataset.shape[1]
#样本数
m = len(dataset)
#多元高斯函数指数前面的部分
first = np.power(2*np.pi,-n/2)*(np.linalg.det(cov)**(-0.5))
#多元高斯函数指数的幂的部分
second = np.zeros((m,1))
for row in range(m):
second[row] = -0.5*(x_u[row]@np.linalg.inv(cov)@x_u[row].T)# * 点乘 @矩阵乘
p = first*np.exp(second)
#方便绘图和操作，变成一维数组
p = p.flatten()
return p
5、绘制等高线，使模型可视化
#图形可视化
def plotGaussian(dataset,u,cov):
x = np.arange(0,30,0.5)
y = np.arange(0,30,0.5)
#生成网格坐标xx,yy
xx,yy = np.meshgrid(x,y)
#获取等高线z值
z = gaussian(np.c_[xx.ravel(),yy.ravel()],u,cov)
zz = z.reshape(xx.shape)
plt.scatter(dataset[:,0],dataset[:,1],marker='+',c='c')
contour_levels = [10**h for h in range(-20,0,3)]
#绘制等高线
plt.contour(xx,yy,zz,contour_levels)
6、在交叉验证集中使用不同的阈值ε，通过F1-score等指标选择合适的ε
#寻找最佳阈值
'''
Label:真实标签
p:计算出来的概率值
上面两个用于计算F1-score
'''
def selectThreshold(Label,p):
bestEpsilon = 0
bestF1 = 0
#设置阈值范围
epsilons = np.linspace(min(p),max(p),1000)
Label = Label.flatten()
epsilons = epsilons.flatten()
for e in epsilons:
p_ = p<e
#预测为1的正样本
tp = np.sum((Label==1)&(p_==1))
#预测为1的负样本
fp = np.sum((Label==0)&(p_==1))
#预测为0的正样本
fn = np.sum((Label==1)&(p_==0))
#精准率(注意分子不能为0)
prec = tp/(tp+fp) if (tp+fp) else 0
#召回率
rec = tp/(tp+fn) if (tp+fn) else 0
#F1得分
F1_score = 2*rec*prec/(prec+rec) if (prec+rec) else 0
if F1_score > bestF1:
bestF1 = F1_score
bestEpsilon = e
return bestEpsilon,bestF1
#获取训练集的u和Σ
u,cov = estimateGaussian(trainData,True)
#获取验证集的运算结果
p = gaussian(valData,u,cov)
#验证集结果和真实标签带入获得最佳阈值
bestEpsilon,bestF1 = selectThreshold(valLabel,p)
#bestEpsilon=9.074844572965703e-05,bestF1=0.8750000000000001
7、选择ε后，对测试集进行预测
#本例子是在训练集做的预测
#5、预测
#获得在训练集的高斯分布结果
p = gaussian(trainData,u,cov)
#找到p<ε的异常值下标
index = np.where(p<bestEpsilon)
#获取异常样本的feature
anmos = trainData[index]
#可视化样本
plotGaussian(trainData,u,cov)
#标红异常点
plt.scatter(anmos[:,0],anmos[:,1],c='r',marker='o')
结果:
完整代码：
import scipy.io as scio
import matplotlib.pyplot as plt
import numpy as np
#导入数据集ex8data1.mat
dataset = scio.loadmat("ex8data1.mat")
#导入的dataset的类型是五、推荐系统
1. 问题描述
有一个电影网站，邀请用户对看过的电影进行评分(0~5)。如下图：
推荐系统问题是：
通过已经评分的电影信息去预测各用户未评分电影的评分。【即预测上图问号的值】
符号描述
（1）nu : 用户数量
（2）nm : 电影数量
（3）r(i,j) = 1 : 第j位用户已经对第i部电影做出评分
（4）y(i,j) : 第j位用户对第i部电影的评分
推荐系统问题的另一种描述:
给出了r(i,j)和y(i,j)数据，然后去查找那些未被评分的电影，并试图预测这些电影的评分。
2. 基于内容的推荐算法
对于用户频分的预测问题，添加两个特征x1、x2对该问题进行描述；x1和x2分别表示爱情指数和动作指数。
因此对每部电影用三个特征进行表示：x0、x1、x2 【x0=1,偏置的权重】
我们可以把每位用户的频分预测看作是一个线性回归问题，因此对第j位用户需要学习参数θ(j)对该用户评分进行预测。
【本实例中nu=4，所以有4个线性回归问题，需要预测4个不同的参数θ】
预测第j位用户对第i部电影的评分可以描述为：(θ(j))T x(i)
例如：
假设
x(3) = [1 0.99 0]T
θ(1) = [0 5 0]T
则第一位用户Alice对第3部电影Cute puppies of love评分预测为:(θ(1))T x(3) = [0 5 0]T*[1 0.99 0] = 4.95
问题描述：
接下来的任务是学习得到θ^(j)^，最小化代价函数，代价函数如下图：
在求θ(j)的过程中，式中的j是固定的；因此求和符号表示的是获取第j位用户已评分电影的序号i。
.
m(j)表示用户评过分的电影数量
.
上图是正则项
m(j)是常数项，并不会影响训练得到的θ(j)，为了简化将m(j)去掉，代价函数变成下图：
对于整个推荐系统来说，需要学习多个θ，因此系统代价函数为单个θ代价函数的总和，系统代价函数如下图第二个式子：
对代价函数进行求导推出梯度下降函数如下图：
【上图梯度下降函数第一个是关于偏置的，偏置不需要正则化。】
3. 协同过滤
对于上述的方法，很难去收集某部电影的爱情指数和动作指数，而且通常我们还需要这两个特征之外的其他特征。
若我们假设每位用户都告诉我们他们喜欢爱情电影的程度和喜欢动作电影的程度。
并且我们假设Alice和Bob十分喜欢爱情电影，Carol和Dave十分喜欢动作电影；于是获得上图的θ值。
【注意：x0=1,偏置的权重】
假设第一部电影是爱情电影，即x1=1.0，x2=0.0；现在想要做的是(θ(1))Tx(1)=5
推荐问题转变成了已知用户偏好，学习电影特征
转变后的推荐问题目标代价函数如下图所示：
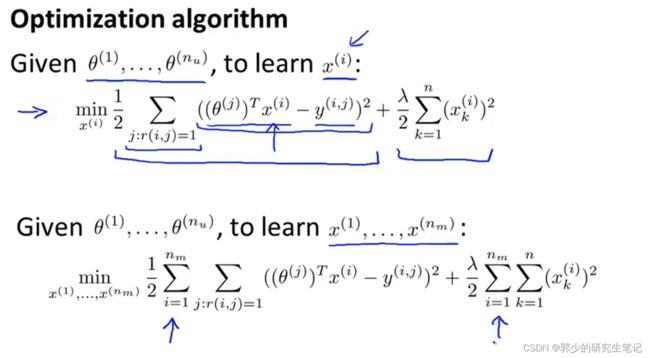
协同过滤：
因此可以先随机猜用户偏好θ的值，然后用于训练电影特征x；在通过x去训练θ值，一直循环反复迭代下去，最后算法会收敛到一组合理的电影特征以及一组合理的对不同用户的参数估计。
上述问题要确立在每位用户对数个电影都进行了评价，并且每部电影都被数位用户评价的基础上。才能够循环迭代估计θ和x
协同过滤算法是指当你执行算法时，要观察大量的用户，观察这些用户的实际行为来协同的得到更佳的每个人对电影的评分值。因为每个用户都对一部分电影做出了评价，那么每个用户都在帮助算法学习出更适合的特征。即通过自己对几部电影进行评分，我就能帮助这个系统更好地学习特征，然后这些特征又能更好的预测其他用户的评分。
4. 协同过滤算法
之前的协同过滤算法需要循环的最小化上图的(1)和(2)代价函数。
为了能够同时计算θ和x，合并(1)和(2)，得到综合化的代价函数(3)；可以发现当我们对x进行求导，θ的正则项就会变成0，代价函数变成了(2)；同理对θ进行求导，x的正则项就会变成0，代价函数变成了(1)；
综合化代价函数不需要迭代的先关于θ最小化，然后在关于x最小化。我们需要做的是关于这两组参数θ和x同时进行最小化。
在这里放弃之前的惯例，去掉x0，则x从n+1维变成了n维；θ同理，舍去θ0。
放弃这个惯例的理由是：
我们现在是在学习所以的特征，没有必要将一个特征硬编码为1；因为如果算法真的需要一个特征永远为1，它可以选择靠自己去获得1这个数值。
协同过滤算法：
5. 向量化：低秩矩阵分解
本小节讨论的是协同过滤算法的向量实现。
对于电影评分信息，我们可以得到矩阵Y
协同过滤算法中还需要获得预测矩阵Predicted ratings来进行梯度下降；Predicted ratings是矩阵x和矩阵θ相乘的结果。如下图：
低秩矩阵表示的就是矩阵x和矩阵θ相乘，因此在讨论低秩矩阵分解时就是在讨论协同过滤算法。
协同过滤算法可以为用户推荐相关的产品(电影)：
（1）如何找到相关的产品：
为每个产品设置特征向量，根据特征向量进行寻找
（2）如何找到与产品j相关的产品i:
可以根据产品之间的距离||x(i)-x(j)||进行寻找
如找到与电影j最相似的5部电影：寻找与电影j有最小距离的电影
6. 实施细节
现在考虑一个问题，如果某位用户没有对任何电影进行评分，协同过滤算法会怎么处理呢？
现在假设电影特征是2维的，即n=2；在θ也是二维的。我们现在要学习出用户Eve的θ(5)
综合代价函数如上图所示。因为用户Eve没有对影片进行评分，因此第一个累加和项不影响θ(5)；只剩下第三个累加和项对θ(5)有影响，因此θ(5)希望能最小化第三个累加和项，即最小化：
最后的结果会是θ(5)=[0 0],然后对用户Eve电影评分的预测都是0，这个结果并没有什么用。
若对评分数据进行均值化：
接下来使用协同过滤学习得到θ和x，用户Eve的θ和x依旧是0，但在预测输出时会加上均值u，因此用户Eve的值会变成大众评分的均值。
7.代码实例
问题描述：
数据集:ex8_movies.mat；
里面包含两个矩阵：Y和R
Y有i行j列，y(i,j)表示第j个用户对第i部电影的评分
R有i行j列，r(i,j)=1表示第j个用户对第i部电影已进行评分
假设电影由十个特征feature，则电影特征矩阵 X = (10,nm) 用户偏好矩阵 θ = (10,nu)
目标：
添加一位新用户并向其推荐10部电影
1、导入数据集
import scipy.io as scio
import matplotlib.pyplot as plt
import numpy as np
#导入数据集ex8data1.mat
dataset = scio.loadmat("ex8_movies.mat")
#导入的dataset的类型是2、序列化和解序列化
使用序列化和解序列化的原因是需要使用minimize来进行迭代梯度下降。
(个人理解)原本我使用for循环进行迭代参数更新，但是发生了错误，参数全部变成了nan，应该是参数迭代过程中某些参数超出了表示范围，因此简单的for循环不能使用，应该使用优化算法minimize来执行梯度下降，而minimize接收的参数要求是一维数据，因此需要将参数进行序列化和解序列化
#1、序列化参数
def serialize(X,Theta):
#将X和Theta变成一维数组在按列合并
return np.append(X.flatten(),Theta.flatten())
#2、解序列化参数
'''
params:X和Theta序列化以后
'''
def deserialize(params,nm,nu,nf):
X = params[:nm*nf].reshape(nf,nm)
Theta = params[nm*nf:].reshape(nf,nu)
#将X和Theta变成原样
return X,Theta
3、代价函数与梯度下降
#3、代价函数与梯度下降
'''
Theta:用户偏好矩阵
X:电影特征矩阵
Y:真实用户评分矩阵
lamda:正则化参数λ
'''
def costFunction(params,Y,R,nm,nu,nf,lamda):
X,Theta = deserialize(params,nm,nu,nf)
#
cost_1 = 0.5*np.square((X.T@Theta-Y)*R).sum()
regu_1 = 0.5*lamda*np.square(X).sum()
regu_2 = 0.5*lamda*np.square(Theta).sum()
cost = cost_1+regu_1+regu_2
return cost
def gradientDescent(params,Y,R,nm,nu,nf,lamda):
X,Theta = deserialize(params,nm,nu,nf)
#X_:X的改变量 Theta_ :Theta的改变量
X_ = Theta@((X.T@Theta-Y)*R).T+lamda*X
Theta_ = X@((X.T@Theta-Y)*R)+lamda*Theta
return serialize(X,Theta)
4、均值归一化
#4、均值归一化
def normalize(Y,R):
#u = np.mean(Y,axis=0)这种方法是错的，r(i,j)=0的地方不算
u = (np.sum(Y,axis=1)/np.sum(R,axis=1)).reshape(-1,1)
Y = (Y-u)*R
return Y,u
5、添加用户
#5、添加新用户
my_ratings = np.zeros((n_m,1))
my_ratings[9] = 5
my_ratings[66] = 5
my_ratings[96] = 5
my_ratings[121] = 4
my_ratings[148] = 4
my_ratings[285] = 3
my_ratings[490] = 4
my_ratings[599] = 4
my_ratings[643] = 4
my_ratings[958] = 5
my_ratings[1117] = 3
#添加新用户信息到矩阵Y和R
Y = np.c_[Y,my_ratings]
R = np.c_[R,my_ratings!=0]
n_u+=1
6、模型训练
#均值归一化
Y,u = normalize(Y,R)
#初始化X和θ矩阵 X:电影特征矩阵(n_f,n_m) Theta(θ):用户偏好矩阵(n_f,n_u) X.T@Theta=预测评分
#X某一列代表一个电影的特征向量 Theta某一列代表一个用户的偏好向量
X = np.random.random((n_f,n_m))
Theta = np.random.random((n_f,n_u))
#8.模型训练
from scipy.optimize import minimize
params = serialize(X,Theta)
lamda = 5
'''
x0:需要更新的参数，得是一维数组
args:传入参数(除了params外按顺序写)
fun :代价函数
jac :梯度下降函数
method :优化方法
'''
res = minimize(x0 = params,
fun = costFunction,
args = (Y,R,n_m,n_u,n_f,lamda),
method = 'TNC',
jac = gradientDescent,
options = {'maxiter': 150})
params_fit = res.x
fit_X,fit_Theta = deserialize(params_fit,n_m,n_u,n_f)#解序列化得到X，Theta
7、预测新用户
#预测填加的用户
#记得加上均值
predict = fit_X.T@fit_Theta+u
#取最后一列
y_pred = predict[:,-1]
#逆序排列
index = np.argsort(-y_pred)
#推荐前十部电影的下标
index[:10]
#读取电影信息文件，主要读取电影名字和年份
with open('movie_ids.txt','r',encoding = 'latin1') as file:
movies = []
for line in file:
str = line.strip().split(' ')
#去掉第一个序号，后面得以空格分隔并加入到列表中
movies.append(' '.join(str[1:]))
#打印输出
for i in range(10):
#输出:序号 电影名词 (年份) 预测评分
print(index[i],movies[index[i]],y_pred[index[i]])
8、实验结果
完整代码
import scipy.io as scio
import matplotlib.pyplot as plt
import numpy as np
#导入数据集ex8data1.mat
dataset = scio.loadmat("ex8_movies.mat")
#导入的dataset的类型是六、大规模机器学习
1. 学习大数据集
为什么要使用大数据集呢？
因为已经知道一种获取高性能的机器学习系统的途径，是采用低偏差的学习算法并用大数据进行训练
数据集很大时，如m为一亿，光计算代价函数就需要很大的计算机资源。在本章将会介绍一种优化的梯度下降算法。
2. 随机梯度下降
原来的梯度下降算法也叫做批量梯度下降(Bath gradient desent)。即同时考虑所有的训练样本。
以线性回归为例子，线性回归算法如下图所示，当m很大时，光计算求和项就需要很大的计算代价。
因此引入随机梯度下降：
随机梯度下降：
- 随机打乱数据集
- 遍历数据集，每遍历一个数据样本就进行梯度下降
- 重复步骤2多次(外层循环一般一次就够，最多不要超过十次)
与批量梯度下降相比，随机梯度下降
不需要对全部m个样本求和来得到梯度项，每遍历一个样本就可以进行梯度下降。
随机梯度下降每次挪动的步子会很小，但是每一次迭代都会很快，因为不需要对所有样本进行求和。
移动的步子会比较曲折，但会在某个范围内朝着局部最小值的方向徘徊
3. Mini-batch梯度下降
Mini-batch梯度下降：
使用一个较小的批量大小进行批量梯度下降。
批量大小b一般取10，常用的取值范围是在2~100之间。
每b个样本进行梯度下降，相比批量梯度下降计算量小。
4.随机梯度下降收敛
在使用样本(x(i),y(i))进行参数更新前，先计算代价函数值cost(θ,x(i),y(i))。
每1000次迭代更新后，计算最近的1000个样本的代价函数的平均值，将该平均值近似为一个大迭代后的代价函数值。
即每1000个样本的代价函数的平均值绘制一个代价函数点。
代价函数图可能如下图所示：
梯度下降最后会在某个代价函数最小值范围进行徘徊，可以使用逐渐缩小的学习率使在最后的递归下降中，代价函数会在一个更小的代价函数最小值范围进行徘徊，使下降过程更加收敛。
5. 在线学习
在线学习例子:
有一个为用户提供快递服务的网站，用户提供发货地、收货地和其他一些信息，然后网站给出服务价格。用户接收网站的服务则y=1，不接受网站的服务则y=0.
现在网站希望能够给出最合理的价格，让用户大概率接受该网站的服务。
在线学习中，每一个用户对该网站进行操作就会获得一份数据样本(无论用户是否使用该网站的服务)，网站每获得一份数据样本就会进行参数更新。
上述的在线学习方式，每获得一份数据，就会进行一次参数更新；使用过的样本都会被丢弃，即训练集样本不固定，当有源源不断的用户可以看作是无限的数据集。
在线学习的优点:
它可以跟进最新的用户偏好，当用户偏好改变了，最新的数据会调整参数从而使模型适应新的训练集数据(新的用户偏好)。
6.减少映射与数据并行
Map-reduce：
有一个大小为400的训练集样本，在使用批量梯度下降时，下降梯度中的求和计算量会很大。
若有4台计算机，可以将训练集分成4个部分分别去计算，再将运算结果发给服务器，由服务器计算最终的下降梯度。
分成4部分由4台计算机分别计算，可以提升4倍的计算速度。
若你想将Map-reduce运用于某种算法上，并通过 多台电脑/多核计算机 并行运算来实现加速，需要考虑一个关键问题:学习算法是否可以表示成对训练集的一种求和
七、应用示例：Photo OCR
1.问题描述与.OCR.pipeline
Photo OCR即照片光学字符识别，照片OCR问题注重的问题是如何让计算机读出图片中的文字信息。
OCR步骤:
（1）扫描图片，找出照片中的文字区域；
（2）重点针对文字区域的文字进行识别；
（3）正确读出文字后显示并记录文字。
机器学习流水线:
流水线的不同模块可以分配不同人员进行。
2.滑动窗口分类器
为了理解文字区域识别，先通过识别行人的例子来解释：
上图可以看到，行人识别的一个特点就是识别的区域有较为类似的长宽比。
接下来从数据集中抽取一些样本用于分类器训练，如下图：
接下来从要识别的图片中分割一块82x36像素的图片，并放到分类器中进行识别，如下图：
分类器会返回y=0表示不是行人，接下来将绿色的框向右移动，再传给分类器进行分类判断。
每次移动的距离是一个参数，一般称之为步长，也可以被称为滑动参数。
将绿色框遍历图中的所有不同位置，并通过分类器进行分类。
但是这个框大小有限，只能识别大小特定的行人。接下来要做的是使用更大的框对图片进行遍历，并进行分类。
最后算法能够检测出图中各个地方是否出现行人
接下来在回到OCR问题，与行人识别一样，需要从数据集中获取一些样本用作分类器训练，如下图：
接下来在测试集图片上使用滑动窗口分类器对图片进行识别分类，下图中，有文本的概率越高，就越亮：
经过放大算子放大后，对长宽比例不太对的白色部分进行去除。最后对剩余的白的部分画上矩形。
将画上矩形的区域剪切出来，进入流水线的第二步—字符分割：
在这里同样需要训练一个分类器模型来判断是否需要进行字符分割，如下图：
之后将文字分割分类器用于需要检测的图片：
如下图，分类器会说no，不需要分割
移动绿色框，分类器输出y=1，需要分割
遍历图片后对图片中文字进行分割：
流水线的最后一步就是文字识别。
整体流程图如下:
3.获取大量数据和人工数据
一个最可靠的得到高性能机器学习系统的方法是使用一个低偏差机器学习算法并且使用庞大的训练集去训练它。
如何获取大量的样本数据呢？
-
自己创造数据，从零生成数据
例如字符识别的例子：
我们可以通过字体库去创造新的数据样本，如将不同字体复制粘贴到不同的背景下，也可以通过旋转、模糊算子或者仿射变换对数据进一步扩充，最终就会得到一个人工合成训练集。
-
已经有小的标签训练集，然后以某种方式扩充训练集
例如：对数据集进行人工拉伸，得到16个新的数据样本
又例如音频样本，可以在原始音频加上不同的背景音
在获取大量数据集的时候，要确保对于测试集来说是典型的，即在真实情况下会出现类似情况，对模型训练有帮助。
最后引入一个名词:人工数据合成
在考虑通过人工数据合成获取更多数据样本时：
（1）先确保你的模型是低偏差的(Low bias)
当模型偏差较高，可以通过增加更多的feature来降低偏差；而不是花大量时间获取更多数据样本，最后模型性能并没有得到很大提升。
先用测试确保需要大量训练数据，再花精力去生成训练样本
（2）思考:获得我当前拥有的数据的10倍的数据量，需要花费多少时间？
获取的方式：人工数据合成、自己收集并标注、Crowd source(众包)
4.上限分析
以照片ORC为例子：
在确定流水线之后，应该分配不同的人力资源到不同的模块，那么那个模块应该分配更多的资源，更值得花费精力呢？这便是上限分析要做的事
如：
目前整体系统正确率为72%(也可以用其他度量来评价系统)，
下面是上限分析的主要思想：
首先我们关注这个机器学习工作流中的第一个模块：文本检测。
我们可以人为的提供100%正确框出字体的数据集，将100%正确的数据集传给下一个模块。接下来继续运行完后面的几个模块，再用之前的评价指标来评级系统。
同理接下来关注下一个模块：字符分割
人工的分割字符，提供100%正确的数据集，然后观察系统的正确率。
【最后的100%即系统的上限】
最后得到：
所以也许我们会把更多资源放在text detection上，有更高的性价比。