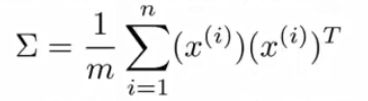吴恩达机器学习笔记之降维

 

第二类无监督学习问题，叫做降维（Dimensionality Reduction）。方法有数据压缩和可视化。

数据压缩：

数据压缩不仅可以减少数据在我们计算机当中的存储空间，还可以加速我们算法的学习过程。

如图所示，我们将三维数据压缩到二维数据。首先我们观察到数据差不多都分布在同一个平面上，因此我们将数据投影到一个二维平面，然后就将可以将三维数据压缩到二维数据。

可视化：

将高维数据降到低维，比如3维或者2维，在进行可视化，便于我们发现找到更好的一个解决方案。

主成分分析（Principal Component Analysis）：

试图找到一个低维数据的平面来对高维数据进行投影。拿下图的二维数据作为例子，我们要做的就是找到一条直线，或者说找到一个方向向量，使得所有数据投影到该方向向量的距离之和最短，这也是我们的目标。

更具体的，当我们要将n维数据压缩到k维数据时，我们的目标是寻找到k个向量，使得原始数据投影到这k个向量的距离之和最短。另外，PCA和我们的线性回归看起来尽管很像，但还是有很大不同的。我们的线性回归的总体目标是最小化样本与模型预测值的差距，而PCA是最小化垂直距离，并没有预测值的概念。另外，在线性回归中，我们的数据是有标签的，而我们的PCA中数据是没有标签的。

 

特征缩放：

接下来我们来看看具体计算过程是怎么样的，如果我们想将n维数据降到k维数据，我们首先要做的是计算协方差矩阵（covariance matrix），是Sigma的大写形式，用来表示一个矩阵。是n*1维的，所以Sigma是一个n*n维的矩阵。

然后我们用奇异值分解[U, S, V] = svd(Sigma)，计算出特征向量U。我们用SVD的原因是因为SVD在数学上总满足正定性。

我们得到特征向量U之后，它的形式如下图所示：

之后我们取特征矩阵的前k列出来作为一个新的矩阵，我们叫做，然后我们新的低维数据表示z = 。

PCA算法总结：对于Sigma的计算，有一种非常好的项量化的计算方式，如下图所示：。

和K-means算法一样，这里的应用向量是，所以。

压缩重现：

当我们将高维数据压缩至低维数据之后，我们应该怎么将低维数据还原成高维数据呢？

低维数据，要求x，易知，但是我们要知道，这里求出的x只是x的近似，如下图所示，求出的x其实是原始数据投影到我们找的向量上的点，而并不是原始的点，但是如果这个投影误差足够小的话我们是可以忽略的，而这也是我们寻找这个向量时所满足的条件，即让投影误差尽可能的小。

主成分数量的选择：

我们在进行主成分分析的时候，我们的目标是为了最小化平均均方投影误差，即

另外还有一个叫做数据的方差：

我们在选择k的值的时候，所希望的是平均均方误差与训练集数据方差的比值小于0.01：

因为这样我们可以保证原始数据百分之99的偏差都被保留了下来，这个值可以随着需求的不同而相应的改变。

我们的算法流程如下，首选选取k=1，然后计算相应的值，最后再看上述等式是否满足，不满足则计算k=2，在验证是否满足，直至寻找到满足条件的最小k值。

但是这个算法的缺点是很明显的，计算效率低下。现在我们看回我们利用SVD求解矩阵U的步骤，其实SVD会返回三个矩阵，其中S矩阵是一个对角矩阵，对角线上全都是特征值。（详情请参考矩阵论当中的矩阵的奇异值分解）

这为我们简化上述算法的计算提供了很大的方便，我们只需要计算上述式子在验证是否满足即可，而无需进行之前复杂的计算。

应用PCA的意见：

PCA的应用：1.压缩数据，加速学习算法的速度；2.可视化数据（可视化数据时，k = 2，或者k = 3）。

我们之前说过PCA可以加速某些学习算法的速度，并且加速的常常是监督学习的算法。

PCA的具体做法是，针对带有标签的数据集，首先取出x，不管y，这时数据集便变成了没有标签的数据集，然后对这个数据集进行降维，降维之后再加入y，构成一组新的监督学习的数据集。然后再用学习算法去学习，如果要预测一个y值，那应该先将x匹配到低维的x，然后在输入模型当中进行预测。

PCA算法的压缩程度大致上在

使用PCA的一种不恰当的方式：防止过拟合。

因为PCA可以减少特征的维度，因此有些人可能会用来将高维特征用低维特征表示，从而拥有更少的特征，来达到防止过拟合的目的。这样做可能有时候会达到一定的效果，但是非常不建议这样做，如果你担心过拟合，那么正则化已经提供了非常好的解决方法。因为PCA在降低数据维度的时候，其实是对数据有损失的，他首先不看你的标签值，即y值，将x降维。但是使用正则化的话可以达到相当好的效果，并且正则化当中是考虑了y值的，没有原始数据信息的丢失。

另一种PCA的错误使用方法是，在设计一个机器学习系统的时候，默认将PCA作为机器学习系统的一部分，比较建议的做法是，首先用原始数据进行学习和分析，只有当需要加速我们的算法，或者降维的时候在考虑使用我们的PCA。