音视频入门（四）-JPEG压缩算法原理

一、JPEG的引入

JPEG属于一种图片压缩格式，之前我们通过对YUV420图像格式的学习，了解了怎么计算一帧YUV图像的大小。假设这里一帧图片的分辨率为1080p，像素格式为YUV420，那么它的大小就应该为192010803/2，大约为3M大小。那么如果帧率为10fps时，一秒钟的大小就为30M。显然，耗费的内存过于庞大。这个时候就应该引入图像压缩的概念，JPEG就是一种最常用的图像压缩格式。

二、JPEG压缩原理简述

在日常生活中所见的压缩有分为有损压缩和无损压缩，JPEG压缩属于有损压缩的一种。有损压缩的原理也就是把原始数据中不重要的部分去掉，这样就可以节省它的内存占用。比如说“3.141592653”这个小数，我们计算的时候可以取“3.14”，这便是一种有损压缩的形式。JPEG压缩的简单原理亦是如此，将图像数据分为重要数据和不重要数据，这里的不重要数据就是人眼不易观察的部分，这里可以适当地去除。如上，便是JPEG压缩设计的简单原理。

三、JPEG压缩的具体步骤

步骤一：图像分割

JPEG算法的第一步，会将一帧完整的图片切割为8*8大小的小块。被切割的这些小块在JPEG压缩的过程中被当作最小处理单元。

步骤二：图片像素格式由RGB转YUV

之前的文章中讲解过RGB转YUV，这里简单说明一下为什么要转成YUV格式。对于我们而言，压缩最重要的是将重要的信息和不重要的信息分开来，YUV格式的图像格式恰好能做到这一点。对于人眼来说，明暗的变化更容易感知，这里相关生物学的知识就不班门弄斧了，因为本人也不是专业的。这里，YUV格式的图片将亮度和色度进行了分离，这样可以方便我们分离开数据的重要程度，从而进行下一步骤的处理。这就是为什么要转成YUV格式。

步骤三：离散余弦变换

下面我们来介绍一下JPEG压缩的核心技术，离散余弦变换（DCT变换）。具体的故事背景感兴趣的自己百度。
前面在步骤一中，我们对图像进行了分割，分成了一个个小块。每一小块中，像素的数值的变化是平滑的。假设这一小块的像素值在79-81之间变化，如果这里用cos函数去模拟这段变化的轨迹，由于块的大小特别小，所以这里cos函数的频率是特别大的，这些变化被称为高频信息。
人眼对于这些高频信息是不敏感的，对低频信息比较敏感。假如将8*8的图像块和你的电脑背景作为对比，这样像素值会出现不平滑的变化，变化很大，这时要用函数组合去拟合这段离散数值时, 就会出现低频信息。
因此, 再结合图像压缩的核心思想, 要用较少的不同数值来表示图像, 就需要找到一种变换, 将图像高频的信息和低频的信息区分开来, 并将人眼不敏感的信息映射到接近或等于0。
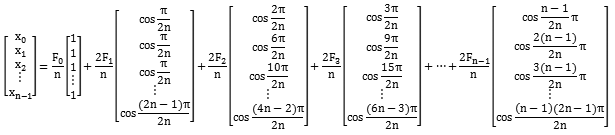
当我们要处理的是一堆离散的数据时，并且这些数据是对称的话，那么傅里叶变化出来的函数只含有余弦项，这种变换称为离散余弦变换。举个例子，有一组一维数据[x0,x1,x2,…,xn-1],那么可以通过DCT变换得到n个变换级数Fi

这个变换是可逆的，原始数据Xi可以通过离散余弦变换变化的逆变换（IDCT)表达出来。

经过DCT变换，可以把一个数组分解成数个数组的和，如果我们数组视为一个一维矩阵，那么可以把结果看做是一系列矩阵的和

经过DCT，杂乱的数据会被转换成几个工整变化的数据。DCT转换后的数组中第一个是一个直线数据，因此又被称为“直流数据”，简称DC，后面的数据被称为“交流数据”，简称AC，这个称呼起源于信号分析中的术语
在JPEG压缩过程中，经过颜色空间的转换，每一个8X8的图像块，在数据上表现为3个8X8的矩阵，紧接着我们对这三个矩阵做一个二维的DCT转换，二维的DCT转换公式为

下面我们做一个实际的测试，比如一个所有数值都一样的矩阵，经过DCT转换后，将所有级数组合成一个新的矩阵

可以看到，经过DCT转换，矩阵的“能量”被全部集中在左上角上的直流分量F(0,0）上，其他位置都变成了0。
在实际的JPEG压缩过程中，由于图像本身的连贯性，一个8X8的图像中的数值一般不会出现大的跳跃，经过DCT转换会有类似的效果，左上角的直流分量保存了一个大的数值，其他分量都接近于0，我们以刚刚那张图片的左上角第一块图像的Y分量为例，经过变换的矩阵为

可以看到，数据经过DCT变化后，被明显分成了直流分量和交流分量两部分，为后面的进一步压缩起到了充分的铺垫作用，可以说是整个JPEG中最重要的一步，后面我们会介绍数据量化。

步骤四：数据量化

刚刚将数据进行了离散余弦变换，并从刚刚的讲述中可以得知，离散余弦变换是有逆过程的。所以上一个步骤是无损的， 真正有损的步骤是在这一步的数据量化。
经过刚刚的格式转换和离散余弦变换后，每一个小图块都变成了3个8*8的浮点矩阵，为什么是3个，因为每个像素点由Y,U,V三个分量组成。它的数据如下

接下来，我要在可以损失一部分精度的情况下，用更小的空间来存储这些数。这个时候我们用到了数据量化。何为量化，就像我们在看小电影的时候，每次快进没有按帧快进，而是按照10s一次往前进。忽略了一些不太必要的细节，从而达到要求，这里就叫量化。JPEG提供的量化算法如下：

其中G是我们需要处理的图像矩阵，Q称作量化系数矩阵，JPEG算法提供了两张标准的量化系数矩阵，分别用于处理亮度数据Y和色度数据U以及V。

亮度量化表

色度量化表

其中round函数是取整函数，但考虑到了四舍五入，也就是说

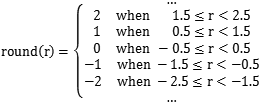
比如上面数据，以左上角的-415.38为例，对应的量子化系数是16，那么round(-415.38/16)=round(-25.96125)=-26。最终得到的量子化后的结果为

可以看到，一大部分数据变成了0，这非常有利于后面的压缩存储。这两张神奇的量化表也是有讲究的，有损压缩就是把数据中重要的数据和不重要的数据分开，然后分别处理。DCT系数矩阵中的不同位置的值代表了图像数据中不同频率的分量，这两张表中的数据时人们根据人眼对不不同频率的敏感程度的差别所积累下的经验制定的，一般来说人眼对于低频的分量必高频分量更加敏感，所以两张量化系数矩阵左上角的数值明显小于右下角区域。在实际的压缩过程中，还可以根据需要在这些系数的基础上再乘以一个系数，以使更多或更少的数据变成0，我们平时使用的图像处理软件在生成jpg文件时，在控制压缩质量的时候，就是控制的这个系数。
在进入下一节之前，矩阵的量化还有最后一步要做，就是把量化后的二维矩阵转变成一个一维数组，以方便后面的霍夫曼压缩，但在做这个顺序转换时，需要按照一个特定的取值顺序。

这么做的目的只有一个，就是尽可能把0放在一起，由于0大部分集中在右下角，所以才去这种由左上角到右下角的顺序，经过这种顺序变换，最终矩阵变成一个整数数组

-26,-3,0,-3,-2,-6,2,-4,1,-3,0,1,5,1,2,-1,1,-1,2,0,0,0,0,0,-1,-1,0,0,0,0,…,0,0

步骤五：编码

JPEG最后一步是对变换,量化后的图像进行编码. 用huffman编码或者其他编码方式, 可以显著节省存储空间。