机器学习02-分类算法

MOOC大学课程 商务数据分析跟学笔记

分类算法

分类算法利用训练样本集获得分类函数即分类器，从而实现将数据集中的样本划分到各个类中。分类模型通过学习训练样本中属性与类别之间的潜在关系，并以此为依据判断新样本属于哪一类

集成学习

集成学习是用多种学习方法的组合来获取比原方法更优的方法，在集合方式上，通常采取数据样本抽样的方式训练多个模型获取综合投票结果，而不采用多个分类器训练相同数据集，因为许多分类器是线性模型，他们最终的投票并不会改进模型的预测结果。

bagging（bootstrap aggregating）

装袋法优于多次采样，每个样本被选中的概率相同，大约有1/3的噪声样本不会被训练，因此噪声数据的影响下降，因所以装袋法不太容易受到过拟合的影响

随机森林在bagging样本抽样的基础上，又增加了属性抽样，增强了样本点随机性，使得整个模型的随机性更强。

boosting

提升法与装袋法相比每次的训练样本均为同一组，并且引入了权重的概念，给每个单独的训练样本都会分配相同的初始权重，然后在多轮训练过程中，对分错的样本权重增加，从而改变样本分布的目的，同时有加速的概念。

Adaboost、GBDT与XGboost

• Adaboost:adaptive boosting，根据前一次的训练结果自适应的更新样本权重。第一次训练时，每个样本权重相同，为1/N，后面迭代时，根据上一次训练结果，增加分错样本的权重，减少分对样本的权重，然后再对所有样本进行训练。

• GBDT 梯度提升决策树
  决策树分为分类树与回归树，分类树的结果不能进行加减运算，回归树的结果是数值，可以进行加减运算，GBDT中的决策树是回归树，损失函数：均方差
  如何在不改变原有模型的结构的基础上提升模型的拟合能力？
  增加一个新的模型，拟合其残差
  思路：利用梯度下降，用损失函数的负梯度在当前模型的值，作为提升树中残差的近似值来拟合回归树
  加法模型

#GBDT XGBOOST示例
import pandas as pd
import xgboost as xgb
df = pd.DataFrame({'x':[1,2,3],'y':[10,20,30]})
x_train = df.drop('y',axis=1)
y_train = df['y']

t_train = xgb.DMatrix(x_train,y_train)
params = {"objective":"reg:linear","booster":"gblinear"}
gbm = xgb.train(dtrain=t_train,params=params)
y_pred = gbm.predict(xgb.DMatrix(pd.DataFrame({'x':[4,5]})))
print(y_pred)
# output:[32.79174 38.75454]

GBDT特点：超参比较多，可用交叉验证的方法选择最佳参数；非线性变换比较多，表达能力强，不需要做复杂的特征工程和特征变换；Boost是串行过程，难以并行化，计算复杂度高，不适合高维稀疏特征；样本中异常值较多时，可将平方损失用绝对损失或Huber损失代替

• XGboost
  XGBoost的boosting策略则与GBDT类似，主要的原理区别是损失函数的不同，GBDT采用梯度下降法，为泰勒公式的一阶展开，通过生成拟合残差的决策树来进行boosting,xgboost的损失函数如下：
  
  采用了泰勒公式的二阶展开，并且增加了正则化项，增强了模型的泛化能力；此外在工程上的优化有：支持列抽样，支持特征粒度并行
  Adaboost、GBDT与XGboost详细参考资料
  GBDT与XGboost的区别

支持向量机

SVM属于有监督学习模型，常用于解决数据分类问题，主要用于二元分类问题
原理
支持向量机在高维空间中构造超平面或超平面集合，将原有限维空间映射到维数更高的空间中，在该空间中进行分离可能会更容易。它可以同时最小化经验误差和最大化集合边缘区，因此也被称为最大间隔分类器

函数间隔:可以表示分类预测的正确性及确信度，支持向量机的学习策略就是分类间隔最大化

线性可分支持向量机(硬间隔)->线性支持向量机(软间隔)->非线性支持向量机(核函数)

• 原理：
  分类超平面$wx+b=0$
  判别函数$y_i=sgn(w{x}_i+b)$
  最大间隔问题，在间隔固定为1时，寻找最小的||w||

优化问题：$min\frac{1}{2}||w|{|}^2$
$s.t.y_i(w{x}_i+b)-1\ge 0$

优化问题引入拉格朗日函数：
$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-{\sum }_{i=1}^n{\alpha }_i(y_i(w{x}_i+b)-1)$
${\alpha }_i$为拉格朗日乘子

分别对$w,b,\alpha 求偏微$

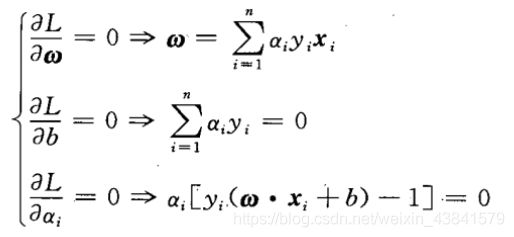
转化为对偶问题：

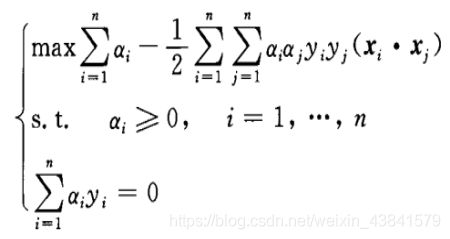
这是一个二次函数寻优的问题，存在最优解，若${\alpha }^{\ast }$为最优解，
$w^{\ast }={\sum }_{i=1}^n{\alpha }^{\ast }{y}_i{x}_i$，再由约束条件${\alpha }_i[y_i(w{x}_i+b)-1]=0$得到最优分类函数为

SVM超详细推导

• 核函数
  将线性不可分数据集映射为线性可分数据集，然后用线性模型做分类
  核函数通俗解释
  线性核函数
  多项式核函数
  径向基核函数
  sigmoid核
• 应用
  svm支持向量机比较适合图像和文本等样本特征较多的应用场合，基于结构风险最小化原理，对样本集进行压缩，解决了以往需要大样本量进行训练的问题。

朴素贝叶斯分类模型

贝叶斯方法用概率表示不确定性，概率规则表示推理或学习，随机变量的概率分布表示推理或学习的最终结果

• 贝叶斯定理：$p(y|x)=\frac{p(x|y)p(y)}{p(x)}$

朴素贝叶斯模型假设特征之间相互独立，那么$p(X|Y)={\Pi }_{i=1}^{n}p(X_i|Y)$，
由于$p(X)$是常数，最终的目标是找到使$p(Y=y){\Pi }_{i=1}^{n}p(X_i|Y=y)$最大的类y

朴素贝叶斯分类模型结构简单，只有两层结构。由于特征向量间的相互独立，算法简单易于实现。同时算法有稳定的分类效率，对于不同特点的数据集其分类性能差别不大。朴素贝叶斯分类在小规模的数据集上表现优秀，并且分类过程时空开销小。算法也适合增量式训练，在数据量较大时，可以人为划分后分批增量训练

• 贝叶斯分类模型过滤垃圾邮件
  假设判断一封邮件E属于垃圾邮件Y=1和非垃圾邮件Y=0的概率，

K近邻

k近邻法不具有显式的学习过程，k近邻实际上利用训练数据集进行特征向量的空间划分，并作为其分类的模型

模型三要素：距离度量，k值，分类决策规则（如多数表决）

PCA和LDA

高维数据降维
指采用某种映射的方法，将原高维空间中的数据映射到低维空间，以减少冗余信息造成的误差，并寻找数据内部的本质结构特征

PCA主成分分析
PCA是最常用的线性降维方法，将高维数据映射到低维空间中，并期望在所投影的维度上数据的方差最大，以此使用较少的维度，同时保留较多的原始数据维度

PCA是一种丢失原始数据最少的线性降维方法，算法目标是求出样本数据协方差矩阵的特征值和特征向量

LDA判断分析
LDA判别分析是一种有监督的线性降维方法，LDA使得同类的投影点尽可能接近，不同类的投影点尽可能远离