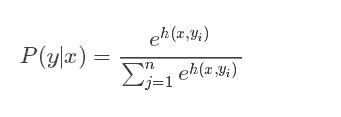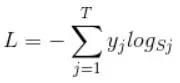深度学习原理24——损失函数与优化过程

1 损失函数的作用

1.1 损失函数的作用就是调整权重

损失函数是用来告诉我们当前分类器性能好坏的评价函数，是用于指导分类器权重调整的指导性函数，通过该函数可以知道该如何改进权重系数。

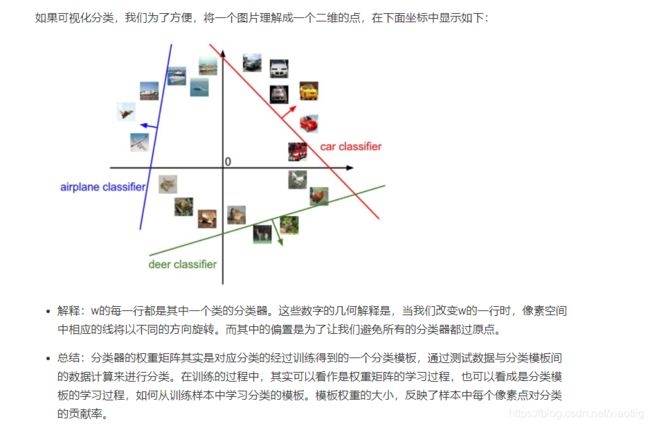
1.2 不同损失函数对应不同的分类器

在图像识别中最常用的两个损失——多类别SVM损失（合页损失hinge loss）和交叉熵损失，分别对应多类别SVM分类器和Softmax分类器。

2 各种损失函数

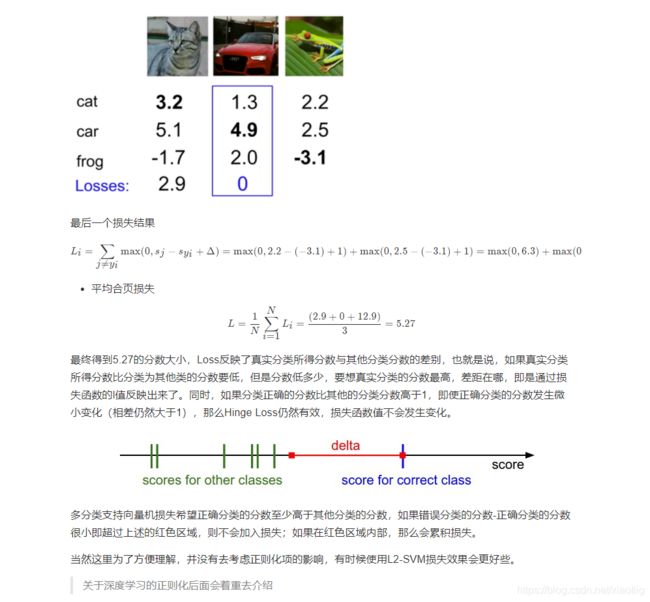
2.1 SVM平均合页损失

2.2 交叉熵损失（softmax分类后）

注意交叉熵是在softmax计算出概率后再用

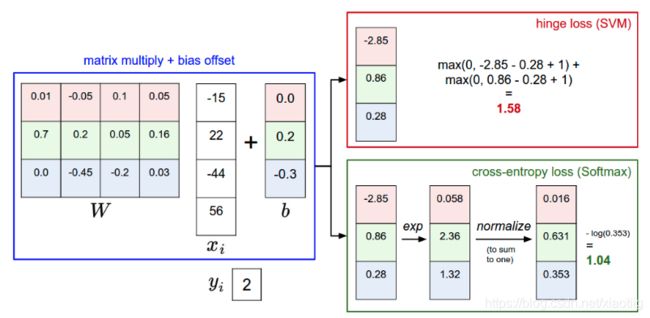
2.3 SVM与Softmax对比

2.4 L1损失：

就是两个值的差的绝对值

2.5 L2损失：

就是两个值的差的平方

2.6 均方误差

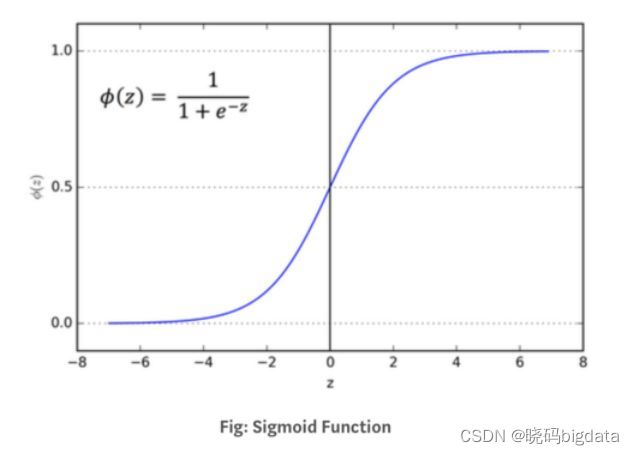
2.7 sigmoid和softmax

1 深度学习的交叉熵损失函数

首先明确一点，进入sigmoid或者softmax的值是多少维度，通过sigmoid或者softmax维度不变，比如sigmoid或者softmax输入前的维度是（256，256，10），通过它们以后输出的维度也是（256，256，10）。 跟给每个数加1的道理一样，只不过对每个数进行了函数变化

在深度学习中，一般来说，无论是用sigmoid和softmax，对应的都是交叉熵损失函数，一个对应
二分类和多分类都叫交叉熵损失函数，一个是sigmoid交叉熵损失函数，一个是softmax交叉熵损失函数
用的是sigmoid，就用binary_cross_entropy
用的是softmax，就用softmax_cross_entropy

2 sigmoid对应binary_cross_entropy

对数函数

sigmoid函数
只为了判断这个值为0或为1

binary_cross_entropy

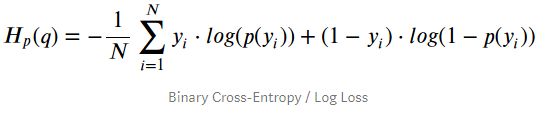
上面的yi表示真实标签，p(yi)表示经过sigmoid后的预测值。
举例：

举个例子，假设一个2分类问题，假如一个batch包含两个样本，第一个样本是类别0，第二个样本是类别1，那么标签要制成一维，形如：
y=[0，1 ]，
模型预测输出也为一维，形如p=[ 0.2，0.6 ] #sigmoid的输出，这里一定要预先用sigmod处理，将预测结果限定在0~1之间。
对应的损失函数值计算：
L=( - 0*log(0.2) - (1 - 0)*log(1- 0.2) - log(0.6) - (1 -1)*log(1 - 0.6) ) / 2 = ( -log(0.8) - log(0.6) ) / 2

极端情况：

L = - 0*log(0.5) - (1 - 0)*log(1- 0.5)=-ln0.5 = ln2

3 softmax对应

softmax函数公式

softmax计算步骤：

假设你的输入S=[1,2,3]，那么经过softmax层后就会得到[0.09,0.24,0.67]，这三个数字表示这个样本属于第1,2,3类的概率分别是0.09,0.24,0.67。

softmax_cross_entropy损失函数计算公式

举例：
**举例1，**softmax计算二分类问题中用了softmax的输出，每个样本输出维2，用sigmoid的时候才为1
假设一个2分类问题，假如一个batch包含两个样本，那么标签要制成二维，
形如y=[ [1, 0]，[0, 1] ]，
模型预测输出也为二维，形如p=[ [0.8,0.2]，[0.4,0.6] ] #（softmax的输出）
那么对应的损失L=( -log(0.8) - log(0.6) ) / 2

**举例2，**多分类，和上面例子计算过程一样
如果3分类问题某个样本预测的logits经过softmax或者sigmoid之后是(0.1, 0.8, 0.1)(这是softmax的结果，sigmoid不保证分量和为1)，而labels的one hot形式是(0, 1, 0)，那么该样本贡献的损失就是-(0ln0.1+1ln0.8+0*ln0.1)/3，batch loss就是一个batch的平均值。可以看出，全预测对，且正确项置信度为1，则loss为0，预测错误损失相当大。

2.8 损失函数大全

语义分割中的 loss function 最全面汇总 - 知乎
https://zhuanlan.zhihu.com/p/101773544

3 网络最优化

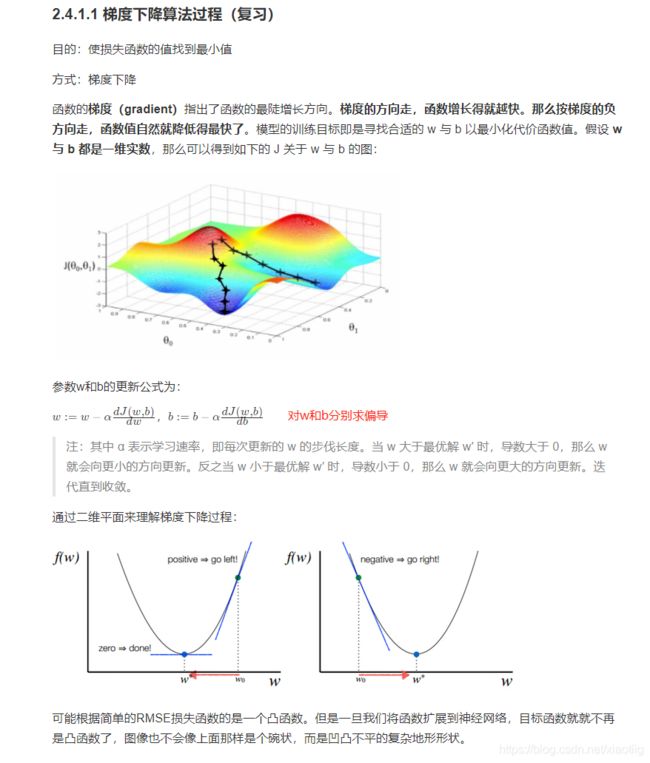
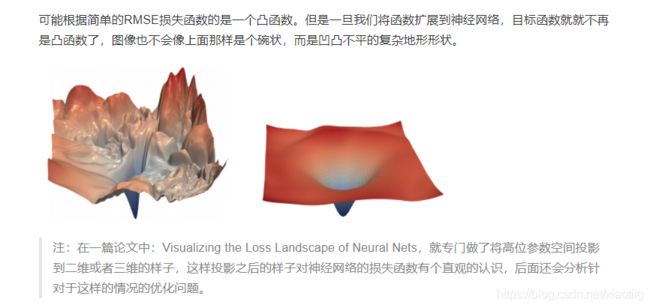
最优化是寻找能使得损失函数值最小化的参数W的过程
目的就是使损失函数最小
转换为更新参数W
方法就是求函数的梯度

3.1 梯度下降

3.2 链式求导与反向传播

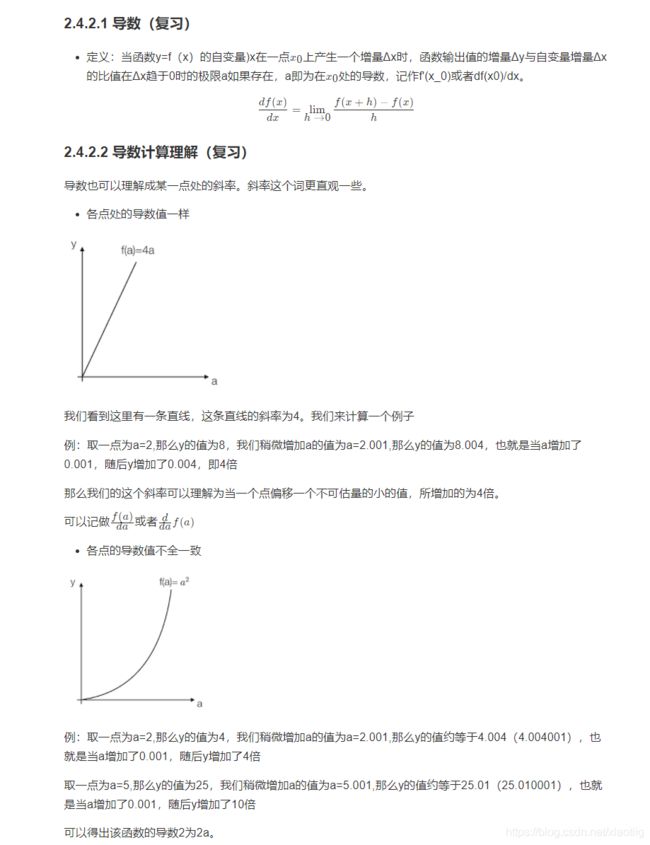
3.2.1 导数与链式求导

3.2.2 反向传播

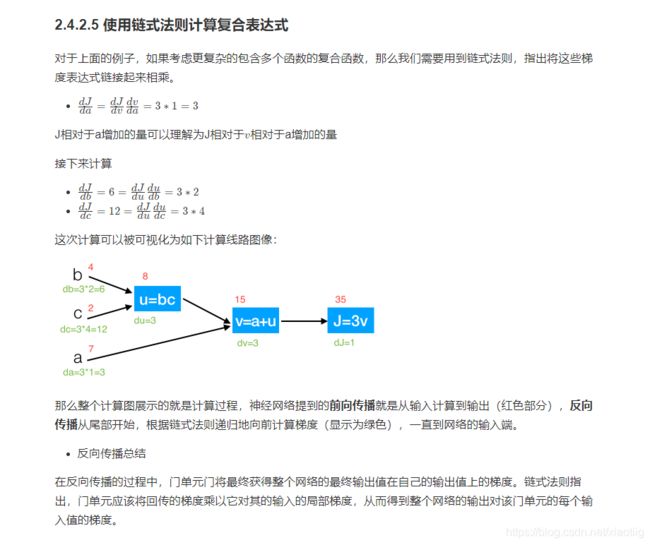
反向传播就是利用链式求导法则进行反向计算

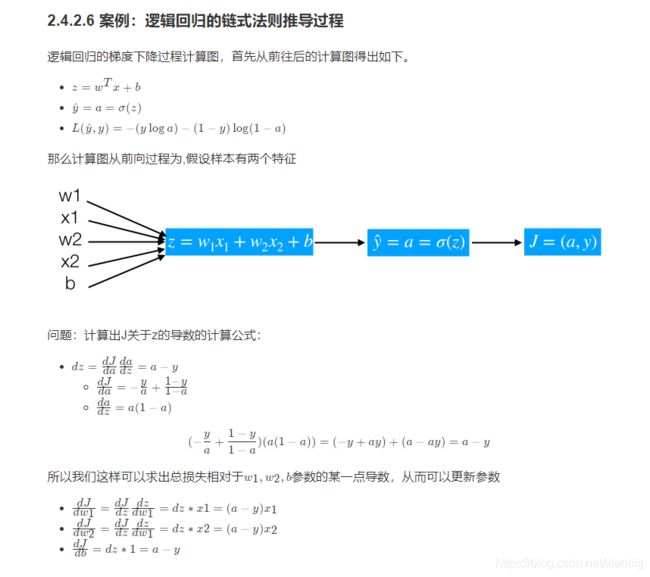
（1）案例：逻辑回归前向与反向传播简单计算
假设简单的模型为y =sigmoid(w1x1+w2x2+b), 我们在这里给几个随机的输入的值和权重，带入来计算一遍，其中在点x1,x2 = (-1 -2)，目标值为1，假设给一个初始化w1,w2,b=(2, -3, -3),由于中间有sigmoid的计算过程，所以我们用代码来呈现刚才的过程。

# 假设一些随机数据和权重，以及目标结果1
w = [2,-3,-3]
x = [-1, -2]
y = 1

# 前向传播
z = w[0]*x[0] + w[1]*x[1] + w[2]
a = 1.0 / (1 + np.exp(-z))
cost = -np.sum(y * np.log(a) + (1 - y) * np.log(1 - a))

# 对神经元反向传播
# 点积变量的梯度, 使用sigmoid函数求导
dz = a - y
# 回传计算x梯度
dx = [w[0] * dz, w[1] * dz]
# #回传计算w梯度
dw = [x[0] * dz, x[1] * dz, 1.0 * dz]

我们可以看出来w1,w2,b是在这次更新是收到x的输入的影响梯度的计算的。

# 随机初始化权重
# w1,w2
W = np.random.random([2, 1])
X = np.random.random([2, 10])
b = 0.0
Y = np.array([0, 1, 1, 0, 1, 1, 0, 1, 0, 0])

Z = np.dot(W.T, X) + b
A = 1.0 / (1 + np.exp(-Z))
cost = -1 / 10 * np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))
# 形状：A:[1, 10] , Y:[1, 10]
dZ = A - Y
# [2, 10] * ([1, 10].T) = [2, 1]
dW = (1.0 / 10) * np.dot(X, dZ.T)
db = (1.0 / 10) * np.sum(dZ)

4 反向传播的代码

一共包括1个文件夹,（datasets文件夹存放了两个h5数据文件）
两个文件

data.py

# 进行数据的读取
import numpy as np
import h5py

def load_dataset():
    train_dataset = h5py.File('datasets/train_catvnoncat.h5', "r")
    train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
    train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels

    test_dataset = h5py.File('datasets/test_catvnoncat.h5', "r")
    test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
    test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels

    classes = np.array(test_dataset["list_classes"][:]) # the list of classes

    print("原始训练数据x的shape:", train_set_x_orig.shape)
    print("原始训练数据y的shape:", train_set_y_orig.shape)
    print("原始测试数据x的shape:", test_set_x_orig.shape)
    print("原始测试数据y的shape:", test_set_y_orig.shape)

    # 把列转换为行
    train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
    test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))

    print("数据转换后训练数据y的shape:", train_set_y_orig.shape)

    return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes

single_unit_nn

## 实现模型的训练

import numpy as np
import data


def main():

    # 1、读取样本数据
    train_x, train_y, test_x, test_y, classes = data.load_dataset()
    print("训练集的样本数: ", train_x.shape[0])
    print("测试集的样本数: ", test_x.shape[0])
    # train_x形状:  (209, 64, 64, 3)
    print("train_x形状: ", train_x.shape)
    # train_y形状:  (1, 209)
    print("train_y形状: ", train_y.shape)

    print("test_x形状: ", test_x.shape)
    print("test_y形状: ", test_y.shape)

    # 输入数据的形状修改以及归一化
    train_x = train_x.reshape(train_x.shape[0], -1).T
    # 这里train_x.shape为(12288, 209)
    test_x = test_x.reshape(test_x.shape[0], -1).T
    train_x = train_x / 255.
    test_x = test_x / 255.

    # 2、模型训练以及预测
    d = model(train_x, train_y, test_x, test_y, num_iterations=2000, learning_rate=0.005)

def model(X_train, Y_train, X_test, Y_test, num_iterations=2000, learning_rate=0.5):
    """
    """
    # 初始化参数
    w, b = initialize_with_zeros(X_train.shape[0])

    # 梯度下降
    # params:更新后的网络参数
    # grads:最后一次梯度
    # costs:每次更新的损失列表
    params, grads, costs = optimize(w, b, X_train, Y_train, num_iterations, learning_rate)

    # 获取训练的参数
    # 预测结果
    w = params['w']
    b = params['b']

    Y_prediction_train = predict(w, b, X_train)
    Y_prediction_test = predict(w, b, X_test)
    print("预测结果是什么：",Y_prediction_test)

    # 打印准确率
    print("训练集准确率: {} ".format(100 - np.mean(np.abs(Y_prediction_train - Y_train)) * 100))
    print("测试集准确率: {} ".format(100 - np.mean(np.abs(Y_prediction_test - Y_test)) * 100))

    d = {"costs": costs,
         "Y_prediction_test": Y_prediction_test,
         "Y_prediction_train": Y_prediction_train,
         "w": w,
         "b": b,
         "learning_rate": learning_rate,
         "num_iterations": num_iterations}

    return d


def basic_sigmoid(x):
    """
    计算sigmoid函数
    """

    s = 1 / (1 + np.exp(-x))

    return s


def initialize_with_zeros(shape):
    """
    创建一个形状为 (shape, 1) 的w参数和b=0.
    return:w, b
    """

    # 本例中shape是209
    w = np.zeros((shape, 1))
    b = 0

    return w, b

def optimize(w, b, X, Y, num_iterations, learning_rate):
    """
    参数：
    w:权重,b:偏置,X特征,Y目标值,num_iterations总迭代次数,learning_rate学习率
    Returns:
    params:更新后的参数字典
    grads:梯度
    costs:损失结果
    """

    costs = []

    for i in range(num_iterations):

        # 梯度更新计算函数
        grads, cost = propagate(w, b, X, Y)

        # 取出两个部分参数的梯度
        # dw的形状是(12288, 1)，每行dw的值是不一样的
        dw = grads['dw']
        db = grads['db']

        # 按照梯度下降公式去计算
        w = w - learning_rate * dw
        b = b - learning_rate * db

        # 每100次输出一次损失
        if i % 100 == 0:
            costs.append(cost)
        if i % 100 == 0:
            print("损失结果 %i: %f" % (i, cost))
            print(b)

    params = {"w": w,
              "b": b}

    grads = {"dw": dw,
             "db": db}

    return params, grads, costs

def propagate(w, b, X, Y):
    """
    参数：w,b,X,Y：网络参数和数据
    Return:
    损失cost、参数W的梯度dw、参数b的梯度db
    """
    m = X.shape[1]

    # w.t的形状 (1, 12288)
    # x的形状： (12288, 209)
    # b就是0：
    # Y的形状： (1, 209)
    # m是个209
    # np.dot(w.T, X)是什么： (1, 209)

    # 前向传播
    # w (n,1), x (n, m)
    A = basic_sigmoid(np.dot(w.T, X) + b)
    # 计算损失
    cost = -1 / m * np.sum(Y * np.log(A) + (1 - Y) * np.log(1 - A))

    # 反向传播
    dz = A - Y
    dw = 1 / m * np.dot(X, dz.T)
    db = 1 / m * np.sum(dz)

    grads = {"dw": dw,
             "db": db}

    return grads, cost

def predict(w, b, X):
    '''
    利用训练好的参数预测

    return：预测结果
    '''

    m = X.shape[1]
    Y_prediction = np.zeros((1, m))
    
    # 计算结果
    A = basic_sigmoid(np.dot(w.T, X) + b)


    # 得分小于0.5归为第一类，大于0.5归为第二类
    for i in range(A.shape[1]):

        if A[0, i] <= 0.5:
            Y_prediction[0, i] = 0
        else:
            Y_prediction[0, i] = 1

    assert (Y_prediction.shape == (1, m))

    return Y_prediction

if __name__ == "__main__":
    main()