【Python】遗传算法求解二元函数最值
序言
遗传算法算是我接触最早的优化算法了,之前大学建模竞赛时学习过,不过当时云里雾里始终没明白其中的原理机制,如今朝花夕拾,看了些博客,又自己动手试了试,总算解决了曾经的困惑。
这里主要参考了(https://blog.csdn.net/ha_ha_ha233/article/details/91364937)的思路,该博主文章写的通俗易懂,建议大家有兴趣的去看看。
我本身不太会Python,借这次机会除了复习遗传算法,也是为了学习Python语法,故我在代码中添加了大量注释,以供同样和我基础薄弱的同学参考,即使你不是为了遗传算法,仅想学习Python知识,相信也能小有裨益。
最后,需要注意的是,本文目的不在于系统阐述遗传算法,一是相关的博客已有很多,二是本人确实没有时间和精力再查阅资料进行系统化规范化论述。本文仅当作一点个人总结,记录和归档。
问题
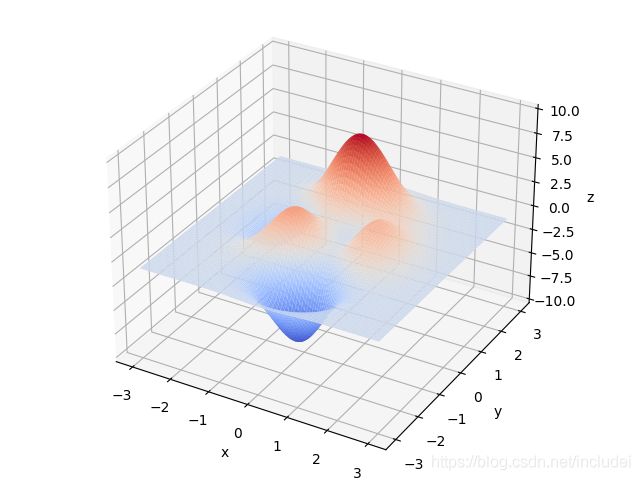
好了,回到正题,这次要解决的问题是求解二元函数的最大值,该函数代码形式如下:
# 问题函数
# @param x x坐标
# @param y y坐标
# @return z 函数值
def problem_function(x, y):
return 3 * (1 - x) ** 2 * np.exp(-(x ** 2) - (y + 1) ** 2)\
- 10 * (x / 5 - x ** 3 - y ** 5) * np.exp(-x ** 2 - y ** 2)\
- 1 / 3 ** np.exp(-(x + 1) ** 2 - y ** 2)
算法步骤
编码和解码
如果把函数的一个解当作个体,种群即是若干个解的集合。对于人来说,我们习惯使用十进制数去计算解决问题,但在计算机中,操作的对象是二进制数,所以把十进制映射到二进制的过程,称为编码;把二进制映射到十进制的过程,称为解码。编码过程暂且省略,因为我们可以直接生成二进制矩阵:
# 生成随机种群矩阵,这里DNA_SIZE * 2是因为种群矩阵要拆分为x和y矩阵,单条DNA(染色体、个体)长度为24
# 若视x和y为等位基因,x和y组成染色体对,共同影响个体,这里巧妙地与遗传信息对应起来
population_matrix = np.random.randint(2, size=(POPULATION_SIZE, DNA_SIZE * 2))
而解码的过程也并不陌生,回想你在学校时学到的进制转换,他们应该是相似的:
# 解码DNA个体
# @param population_matrix 种群矩阵
# @return population_x_vector, population_y_vector 种群x向量,种群y向量
def decoding_DNA(population_matrix):
x_matrix = population_matrix[:, 1::2] # 矩阵分割,行不变,抽取奇数列作为x矩阵
y_matrix = population_matrix[:, 0::2] # 矩阵分割,行不变,抽取偶数列作为y矩阵
# 解码向量,用于二进制转十进制,其值为[2^23 2^22 ... 2^1 2^0],对位相乘累加,二进制转十进制的基础方法
decoding_vector = 2 ** np.arange(DNA_SIZE)[::-1]
# 种群x向量,由二进制转换成十进制并映射到x区间
population_x_vector = x_matrix.dot(decoding_vector) / (2 ** DNA_SIZE - 1)\
* (X_RANGE[1] - X_RANGE[0]) + X_RANGE[0]
# 种群y向量,由二进制转换成十进制并映射到y区间
population_y_vector = y_matrix.dot(decoding_vector) / (2 ** DNA_SIZE - 1)\
* (Y_RANGE[1] - Y_RANGE[0]) + Y_RANGE[0]
return population_x_vector, population_y_vector
交叉和变异
了解了编码解码,你已经可以获得便捷操作二进制的能力,如同装备了片手剑,你才有信心接受怪物的毒打,哦,我是说,你拥有了击败恶龙的可能。让我们进入到遗传算法更核心的部分,交叉和变异。
更接近本质一点,如果把一个解看作DNA(基因,染色体,个体,我知道他们的包含关系,这里不是严谨的比喻,只是为了用生物学相关的概念去类推算法的过程),在种群更迭,遗传的过程中,一定概率下,基因会发生交叉和变异,我们需要模拟的就是这个过程。孩子的基因除了来自父亲,还有部分通过交叉获得的母亲的基因,这里的父母只是一个区别性描述,你可以随意倒换。那么我们就可以操纵代码执行交叉操作:
# DNA交叉
# @param child_DNA 孩子DNA
# @param population_matrix 种群矩阵
def DNA_cross(child_DNA, population_matrix):
# 概率发生DNA交叉
if np.random.rand() < CROSS_RATE:
mother_DNA = population_matrix[np.random.randint(POPULATION_SIZE)] # 种群中随机选择一个个体作为母亲
cross_position = np.random.randint(DNA_SIZE * 2) # 随机选取交叉位置
child_DNA[cross_position:] = mother_DNA[cross_position:] # 孩子获得交叉位置处母亲基因
变异是对DNA的不稳定复制,也就是说,他是DNA自身的改变,同时它发生的概率极低,变异可能往好的或坏的方向发展,但总是不尽如人意,我们也可以模拟这个过程:
# DNA变异
# @param child_DNA 孩子DNA
def DNA_variation(child_DNA):
# 概率发生DNA变异
if np.random.rand() < VARIATION_RATE:
variation_position = np.random.randint(DNA_SIZE * 2) # 随机选取变异位置
child_DNA[variation_position] = child_DNA[variation_position] ^ 1 # 异或门反转二进制位
自然选择
交叉和变异是遗传中种群的自我迭代,但是,不能忘了环境的选择作用,否则,进化将朝着随机的方向不稳定地进行,所谓“适者生存”,环境的选择使种群朝特定的方向演化,回到问题中来,这样的选择作用帮助我们一步步找到最值的近似。
然而,怎么确定谁走谁留?这里,就需要提到适应度,它是环境选择个体的概率,该问题中,我们的适应度,其实就是接近最值的程度,越接近,留存的概率越大,其“优秀基因”也就越能流传下去,获取适应度过程如下:
# 获取适应度向量
# @param population_matrix 种群矩阵
# @return fitness_vector 适应度向量
def get_fitness_vector(population_matrix):
population_x_vector, population_y_vector = decoding_DNA(population_matrix) # 获取种群x和y向量
fitness_vector = problem_function(population_x_vector, population_y_vector) # 获取适应度向量
fitness_vector = fitness_vector - np.min(fitness_vector) + 1e-3 # 适应度修正,保证适应度大于0
return fitness_vector
知道了适应度,接下来要做的事情就很明显了,即无情的自然选择,说无情亦有情,它既不顾个体情感,唯适应度选择,又留有一线生机,不绝对否定或绝对肯定,一切都是概率。接下来就是无保底抽卡时刻:
# 自然选择
# @param population_matrix 种群矩阵
# @param fitness_vector 适应度向量
# @return population_matrix[index_array] 选择后的种群
def natural_selection(population_matrix, fitness_vector):
index_array = np.random.choice(np.arange(POPULATION_SIZE), # 被选取的索引数组
size=POPULATION_SIZE, # 选取数量
replace=True, # 允许重复选取
p=fitness_vector / fitness_vector.sum()) # 数组每个元素的获取概率
return population_matrix[index_array]
至此,我们已经完成了种群的一次完整迭代,剩下的就是重复这个过程不断优化种群,我们迭代次数越多,结果越准确,当然不可能永远迭代下去,那样即使得出完美答案也没有了意义,为平衡时间代价和准确度,通常我们选取一个合适的迭代值,如50,100。
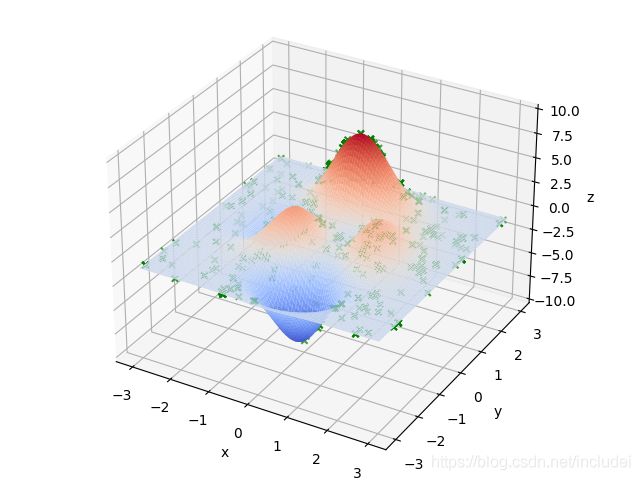
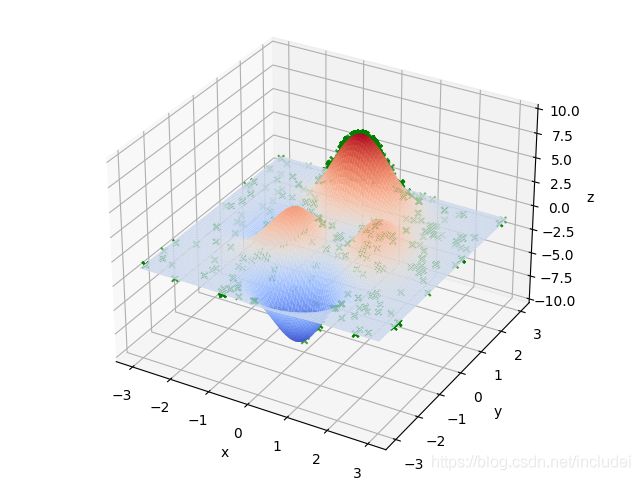
结果
最佳适应度为: 8.142268067060922
最优基因型为: [1 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 0 0 1 1 1 0 0
0 1 0 0 0 1 0 1 1 0 0]
最优基因型十进制表示为: (0.0029763581142638884, 1.5702061993006584)
源码
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
DNA_SIZE = 24 # 个体编码长度
POPULATION_SIZE = 200 # 种群大小
GENERATION_NUMBER = 50 # 世代数目
CROSS_RATE = 0.8 # 交叉率
VARIATION_RATE = 0.01 # 变异率
X_RANGE = [-3, 3] # X范围
Y_RANGE = [-3, 3] # Y范围
# 问题函数
# @param x x坐标
# @param y y坐标
# @return z 函数值
def problem_function(x, y):
return 3 * (1 - x) ** 2 * np.exp(-(x ** 2) - (y + 1) ** 2)\
- 10 * (x / 5 - x ** 3 - y ** 5) * np.exp(-x ** 2 - y ** 2)\
- 1 / 3 ** np.exp(-(x + 1) ** 2 - y ** 2)
# 初始化图
# @param ax 3D图像
def init_graph(ax):
x_sequence = np.linspace(*X_RANGE, 100) # 创建x等差数列
y_sequence = np.linspace(*Y_RANGE, 100) # 创建y等差数列
x_matrix, y_matrix = np.meshgrid(x_sequence, y_sequence) # 生成x和y的坐标矩阵
z_matrix = problem_function(x_matrix, y_matrix) # 生成z坐标矩阵
# 创建曲面图,行跨度为1,列跨度为1,设置颜色映射
ax.plot_surface(x_matrix, y_matrix, z_matrix, rstride=1, cstride=1, cmap=plt.get_cmap('coolwarm'))
ax.set_zlim(-10, 10) # 自定义z轴范围
ax.set_xlabel('x') # 设置x坐标轴标题
ax.set_ylabel('y') # 设置y坐标轴标题
ax.set_zlabel('z') # 设置z坐标轴标题
plt.pause(3) # 暂停3秒
plt.show() # 显示图
# 解码DNA个体
# @param population_matrix 种群矩阵
# @return population_x_vector, population_y_vector 种群x向量,种群y向量
def decoding_DNA(population_matrix):
x_matrix = population_matrix[:, 1::2] # 矩阵分割,行不变,抽取奇数列作为x矩阵
y_matrix = population_matrix[:, 0::2] # 矩阵分割,行不变,抽取偶数列作为y矩阵
# 解码向量,用于二进制转十进制,其值为[2^23 2^22 ... 2^1 2^0],对位相乘累加,二进制转十进制的基础方法
decoding_vector = 2 ** np.arange(DNA_SIZE)[::-1]
# 种群x向量,由二进制转换成十进制并映射到x区间
population_x_vector = x_matrix.dot(decoding_vector) / (2 ** DNA_SIZE - 1)\
* (X_RANGE[1] - X_RANGE[0]) + X_RANGE[0]
# 种群y向量,由二进制转换成十进制并映射到y区间
population_y_vector = y_matrix.dot(decoding_vector) / (2 ** DNA_SIZE - 1)\
* (Y_RANGE[1] - Y_RANGE[0]) + Y_RANGE[0]
return population_x_vector, population_y_vector
# DNA交叉
# @param child_DNA 孩子DNA
# @param population_matrix 种群矩阵
def DNA_cross(child_DNA, population_matrix):
# 概率发生DNA交叉
if np.random.rand() < CROSS_RATE:
mother_DNA = population_matrix[np.random.randint(POPULATION_SIZE)] # 种群中随机选择一个个体作为母亲
cross_position = np.random.randint(DNA_SIZE * 2) # 随机选取交叉位置
child_DNA[cross_position:] = mother_DNA[cross_position:] # 孩子获得交叉位置处母亲基因
# DNA变异
# @param child_DNA 孩子DNA
def DNA_variation(child_DNA):
# 概率发生DNA变异
if np.random.rand() < VARIATION_RATE:
variation_position = np.random.randint(DNA_SIZE * 2) # 随机选取变异位置
child_DNA[variation_position] = child_DNA[variation_position] ^ 1 # 异或门反转二进制位
# 更新种群
# @param population_matrix 种群矩阵
# @return new_population_matrix 更新后的种群矩阵
def update_population(population_matrix):
new_population_matrix = [] # 声明新的空种群
# 遍历种群所有个体
for father_DNA in population_matrix:
child_DNA = father_DNA # 孩子先得到父亲的全部DNA(染色体)
DNA_cross(child_DNA, population_matrix) # DNA交叉
DNA_variation(child_DNA) # DNA变异
new_population_matrix.append(child_DNA) # 添加到新种群中
new_population_matrix = np.array(new_population_matrix) # 转化数组
return new_population_matrix
# 获取适应度向量
# @param population_matrix 种群矩阵
# @return fitness_vector 适应度向量
def get_fitness_vector(population_matrix):
population_x_vector, population_y_vector = decoding_DNA(population_matrix) # 获取种群x和y向量
fitness_vector = problem_function(population_x_vector, population_y_vector) # 获取适应度向量
fitness_vector = fitness_vector - np.min(fitness_vector) + 1e-3 # 适应度修正,保证适应度大于0
return fitness_vector
# 自然选择
# @param population_matrix 种群矩阵
# @param fitness_vector 适应度向量
# @return population_matrix[index_array] 选择后的种群
def natural_selection(population_matrix, fitness_vector):
index_array = np.random.choice(np.arange(POPULATION_SIZE), # 被选取的索引数组
size=POPULATION_SIZE, # 选取数量
replace=True, # 允许重复选取
p=fitness_vector / fitness_vector.sum()) # 数组每个元素的获取概率
return population_matrix[index_array]
# 打印结果
# @param population_matrix 种群矩阵
def print_result(population_matrix):
fitness_vector = get_fitness_vector(population_matrix) # 获取适应度向量
optimal_fitness_index = np.argmax(fitness_vector) # 获取最大适应度索引
print('最佳适应度为:', fitness_vector[optimal_fitness_index])
print('最优基因型为:', population_matrix[optimal_fitness_index])
population_x_vector, population_y_vector = decoding_DNA(population_matrix) # 获取种群x和y向量
print('最优基因型十进制表示为:',
(population_x_vector[optimal_fitness_index], population_y_vector[optimal_fitness_index]))
if __name__ == '__main__':
fig = plt.figure() # 创建空图像
ax = Axes3D(fig) # 创建3D图像
plt.ion() # 切换到交互模式绘制动态图像
init_graph(ax) # 初始化图
# 生成随机种群矩阵,这里DNA_SIZE * 2是因为种群矩阵要拆分为x和y矩阵,单条DNA(染色体、个体)长度为24
# 若视x和y为等位基因,x和y组成染色体对,共同影响个体,这里巧妙地与遗传信息对应起来
population_matrix = np.random.randint(2, size=(POPULATION_SIZE, DNA_SIZE * 2))
# 迭代50世代
for _ in range(GENERATION_NUMBER):
population_x_vector, population_y_vector = decoding_DNA(population_matrix) # 获取种群x和y向量
# 绘制散点图,设置颜色和标记风格
ax.scatter(population_x_vector,
population_y_vector,
problem_function(population_x_vector, population_y_vector),
c='g',
marker='x')
plt.show() # 显示图
plt.pause(0.1) # 暂停0.1秒
population_matrix = update_population(population_matrix) # 更新种群
fitness_vector = get_fitness_vector(population_matrix) # 获取适应度向量
population_matrix = natural_selection(population_matrix, fitness_vector) # 自然选择
print_result(population_matrix) # 打印结果
plt.ioff() # 关闭交互模式
plt.show() # 绘制结果