基于 BP 神经网络基本原理拟合确定函数

  BP（back propagation）即反向传播，是一种按照误差反向传播来训练神经网络的一种方法，BP神经网络应用极为广泛。

BP 神经网络主要可以解决以下两种问题：
1.分类问题：用给定的输入向量和标签训练网络，实现网络对输入向量的合理分类。
2.函数逼近问题：用给定的输入向量和输出向量训练网络，实现对函数的逼近。

本文主要介绍 BP 算法实现函数逼近问题。

一.函数基本逻辑介绍

a.基本输入输出：
一般神经元模型包含这样几个要素：
1.输入：X1、X2、X3…Xn（可以有多个，在这里取两个。如下指令所示，X1、X2都为随机数据，）
2.权重：W1、W2、W3…Wn。
3.偏置：Bias。
4.激活函数：f(x)。
（这里需要重点说明的是激活函数。在笔者的算法中不加入非线性激活函数，只是简单的对输入进行加权求和，整个模型就是个线性模型，而线性模型的表示能力是非常有限的，因此通过加入激活函数的方式给模型引入非线性因素，以提高模型的表示能力，所以一般情况下会采用非线性函数作为激活函数。 常见的激活函数有 Sigmoid、Tanh、Step、ReLU、Softmax 等。 ）
5.输出：y（仅一个）。
b.拟合算法目标：
目标函数：设定一个预设的目标函数g(i)，训练随机数与g(i)相等。
算法输入两个随机数据data，并设定一个预设的目标函数g(i)，i是从0开始的自然数，对拟合成功次数计数,每次随机数拟合的目标函数为g（i）。循环拟合过程，直到拟合成功。函数拟合逻辑如下所示：

不等于

等于

输入两个随机数x1,x2

X1W1+X2W2+X3*W3+Bias

等于待拟合函数吗?

两值求差

调整权重

打印输出,i++,拟合下一个函数值

如上图，我们先把第一组 data 代入函数模型，根据前面所说的计算神经元输出的方法进行计算:
*`int sumfun(int *data,int weight,int bias)
{

return (data[0]*weight[0]+data[1]*weight[1]+bias);

}`
得到实际输出,
实际输出 realoutput 和期望输出 aimoutput (预设的函数)之间就存在一个差值 err=aimoutput1-realoutput。

根据这个差值，可以通过如下公式来修正我们随机给定的权值和偏置：
W=W+etaerrdata
Bias=Bias+eta*err

这里的 eta 表示学习率，一般取 0~1 之间的值。eta 值越大学习速率也越快，也就是每一次训练，权值和偏置的变动越大，但也并不是越大越好。如果 eta 过大容易产生震荡而不能稳定到目标值，若 eta 值越小，则效果相反。这里我们简单的取 eta=1，带入计算式可得经过一次修正过后的权值和偏置，以此类推。
主函数中设置了两组值，分别去拟合两个相同的函数，效果完全相同。是为了调用graphics.h图形库绘制函数时候更为方便。graphics.h库需要自己导入g++根文件中，且需要g++编译参数-lpthread
二.运行结果展示：
请注意graphics.h库默认左上角为坐标原点，并以竖直方向为x轴绘制函数，且由于显示的比例问题，下图为拟合的都是伸缩变换过的函数：
下图拟合的是二次幂函数，反正切函数，和X^x的图像，如下所示：

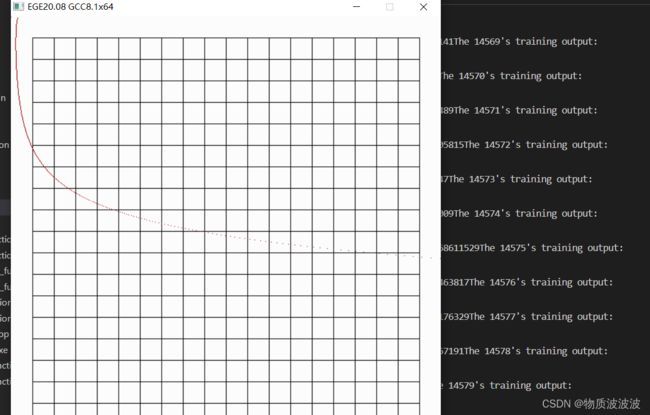三.源代码展示：

#include 
#include 
 #include
 #include
//定义训练用的数据
int data1[2]={rand(),rand()};
int data2[2]={rand(),rand()};
int w[2]={0,0};         
int data1_class=0;      
int data2_class=0; 
//这里用任意值初始化即可，训练的目的就是自动调整这个值的大小
int b=0;  
//加权求和
int sumfun(int *data,int *weight,int bias)
{    
	return (data[0]*weight[0]+data[1]*weight[1]+bias);
}
//这里采用线性函数作为激活函数
int step(int sum)
{    
	return sum;
    }
int main(){ 
   int st = 30;

	initgraph(600,600);//初始化窗口大小
	setbkcolor(WHITE);//背景颜色
	
	setlinestyle(PS_SOLID,2);//设置成实线，宽度为2个像素实线的粗细
	setcolor(RGB(0,0,0));//设置成黑色，前景颜色 不能用setlinrcolor因为没有定义line
	for (int t = 1; t <= 19; t++)
	{
		line(t*st,st,t*st,19*st);//x改变，平行于与y轴的线
		line(st, t * st, 19 * st, t * st);//y改变，平行于x轴的线
    }


      int i=0;
 
   
	int sum=0;                //存放加权求和的值
    int output1,output2;  //把加权求和的值代入激活函数而得到的输出值
    int count=0;                 //训练次数的计数变量
    int err=0;                //计算的误差，用于对权值和偏置的修正
    int flag1=0,flag2=0;         //训练完成的标志，如果某组数据训练结果达标，则把标志置1，否则置0
 
	
	


    while(1)
    {   
         
        sum=sumfun(data1,w,b);  //代入第一组data进行计算
        output1=step(sum);   
               printf("out2=%d",output1);
            
		if(output1==data1_class)//判断输出是否达标，若达标则把标志置1，否则修正权值和偏置
            flag1=1; 
           else
        {
            flag1=0;
            err=data1_class-output1;
            w[0]=(w[0]+err*data1[0])%1;
            w[1]=w[1]+err*data1[1];
            b=b-err;
        }
 
        sum=sumfun(data2,w,b);  //代入第二组data进行计算
        output2=step(sum);        
          printf("out2=%d",output2);
            printf("out1=%d",output1);
            
		if(output2==data2_class)//判断输出是否达标，若达标则把标志置1，否则修正权值和偏置
            {flag2=1; 
                  }
		else
        {
            flag2=0;
            err=data2_class-output2;
            w[0]=w[0]+err*data2[0];
            w[1]=w[1]+err*data2[1];
            b=b-err;
            printf("out2=%d",output2);
            printf("out1=%d",output1);
        }        
		printf("The %d's training output:\n",count+=1);       //输出训练结果
        printf("    First Group's data belongs to %1.0f class.\n",output1);        
		printf("    First Group's data belongs to %1.0f class.\n",output2);        
		if(flag1==1&&flag2==1)   //如果所有数据都训练达标，
        {        i++;
         data1_class=100*atan(0.05*i);      
         data2_class=100*atan(0.05*i); 
			printf("The traning done!");
            printf("out2=%d",output2);
            printf("out1=%d",output1);
            printf("i=%d",i);
            	setcolor(BLUE);
	line(output2,i,output1,i);
	

        }
        
    }     
	    
    return 0;
}

如果要修改拟合的函数，只需要在打印条件中修改

data1_class=目标函数;
data2_class=目标函数;
即可。

文章仅做学习讨论，不可做商业用途。
参考文献：http://mp.weixin.qq.com/s/9AUioTRWSAvKDCd5hPymHQ