利用MATLAB模糊控制器实现对水位高度调节SIMULINK仿真（隶属度7分级）

A.理论分析与设计

 

（1）确定模糊控制器的输入、输出变量

模糊控制器的两个输入变量，分别选为液位偏差E(设定液位高度r-实测液位高度y)和液位偏差变化率EC，输出模糊变量为控制阀门开度U；

（2）确定输入、输出语言变量的空间分割

液位偏差E对应语言变量为Level，其论域为X={-1,-0.6667,-0.3333,0,0.3333,0.6667,1}，对应的语言值为 {PB,PM,PS,ZO,NS,NM,NB}，分别表示当前水位高，较高，偏高，正好，偏低，较低，低；液位偏差变化率EC对应语言变量为EC，其论域为Y={-0.1,-0.03333,0,-0.03333, 0.1}，对应的语言值为{NB, NS,ZO,PS,PB}，分别表示当前水位快速下降、下降、不变、上升、快速上升。控制器输出为控制阀门开度U，对应语言变量为U，其论域为{-3,-2,-1,0,1,2,3}，对应语言值为{NB,NM,NS,ZO,PS,PM,PB}，分别表示“快关阀门”、 “中关阀门”、“慢关阀门”、“阀门开度不变”、“慢开阀门”、“中开阀门”、“快开阀门”。

（3）确定语言值的隶属度函数

Level和EC用高斯型隶属函数，U用三角形隶属度函数。

（4）确定液位模糊控制器的结构

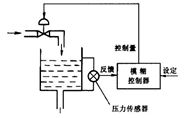
       如图1所示为根据（1）-（3）分析设计的液位模糊控制器的结构，虚线框中的为模糊控制器，执行机构为阀门，被控对象为水箱的液位高度。r(t)为给定液位高度，e(k)为液位偏差的原始信号。 

 图1 液位模糊控制器的结构

 B.FUZZY控制器设计

（1）FUZZY控制器结构

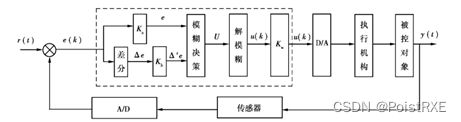
       如图2所示，FUZZY控制器结构采用二维模糊控制器，输入变量为误差Level及误差变化率EC，输出变量为阀门开度U，FUZZY控制算法为Mamdani的关系矩阵法。Level和EC用高斯型隶属函数，U用三角形隶属度函数。解模糊化方法为中位数法。

 图2 FUZZY控制器结构

（2）建立隶属度函数

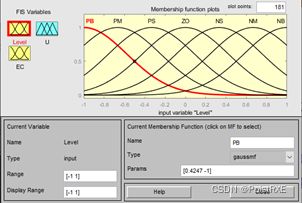
       参照“A.理论分析与设计”中的第（2）步设置相关参数的设置，如图3所示为level的隶属度函数设置。

图3 level的隶属度函数设置

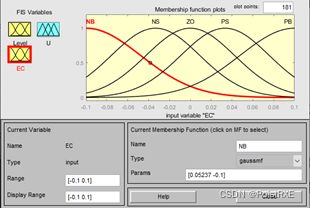
       如图4所示为rate的隶属度函数设置。

图4 rate的隶属度函数设置

如图5所示为valve的隶属度函数设置。

图5 valve的隶属度函数设置

       （3）建立液位模糊控制规则表

表1 液位模糊控制规则表

Level   U EC	NB	NM	NS	ZO	PS	PM	PB
NB	PB	PM	PM	PS	PS	ZO	NS
NS	PM	PM	PS	PS	ZO	NS	NS
ZO	PM	PS	PS	ZO	NS	NS	NM
PS	PM	PS	PS	ZO	NS	NM	NM
PB	PS	ZO	NS	NS	NM	NM	NB

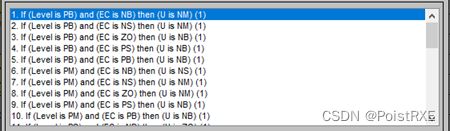
在FUZZY控制器中填写该表格，如图6所示为部分rule设置。

图6 部分rule设置

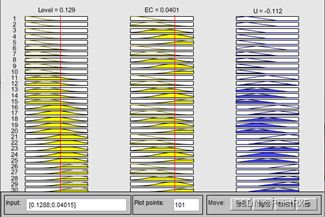
       在view中查看Rules，如图7所示。

图7 RULES实例

在view中查看FIS输出量曲面观测窗，如图8所示为surface观测窗。

图8 surface观测窗

       （4）输出FUZZY控制器

       顺序单击File--Export --To Workspace和To File，将模糊控制器保存为E_EC_U， 模糊控制器设计完毕。

C. 建立基于模糊控制器的液位模糊控制的Simulink模型

（1）搭建Simulink模型

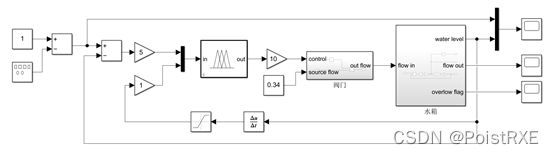
如图9所示为液位模糊控制的Simulink整体框图。

图9 Simulink整体框图

       （2）阀门子系统框图、限幅积分器的参数设置、水箱子系统框图、限幅积分器的参数设置、Overflow sensor参数设置、Signal Generator、Saturation参数设置与利用MATLAB模糊控制器实现对水位高度调节SIMULINK仿真（隶属度3分级）_PoistRXE的博客-CSDN博客利用MATLAB模糊控制器实现对水位高度调节SIMULINK仿真（隶属度3分级）https://blog.csdn.net/qq_42816065/article/details/122397812相同，这里不做累述。如图10所示为Fuzzy Logic Controller参数设置界面。

图10 Fuzzy Logic Controller参数设置

D. Simulink仿真结果

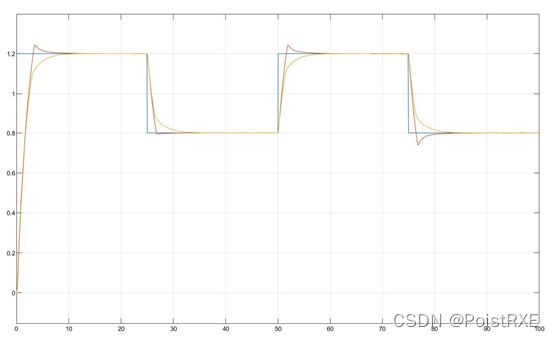
       如图11所示为Simulink仿真结果，蓝色的线给定输入，黄色的线实际液位的变化，橙色的为示例6.1的液位变化结果。可以从结果中看出该模糊控制器能够实现无静差控制，快速性较好，但是出现超调。与示例6.1中的模糊控制器相比，该模糊控制器快速性更好，但是出现了超调。这是因为控制规则中误差起的作用大，可以使系统尽快能够快速调节液位，同时增大了超调。所以该模糊控制器适用于液位偏差较大，系统远离稳态的情况。

 图14 Simulink仿真结果