计算ln_BN,LN,IN,GN都是什么?不同归一化方法的比较
批处理归一化(BN)已经成为许多先进深度学习模型的重要组成部分,特别是在计算机视觉领域。它通过批处理中计算的平均值和方差来规范化层输入,因此得名。要使BN工作,批大小必须足够大,通常至少为32。但是,在一些情况下,我们不得不满足于小批量:
当每个数据样本高度消耗内存时,例如视频或高分辨率图像
当我们训练一个很大的神经网络时,它只留下很少的GPU内存来处理数据
因此,我们需要BN的替代品,它能在小批量下很好地工作。组归一化(GN)是一种最新的规范化方法,可以避免利用批处理维,因此与批处理大小无关。
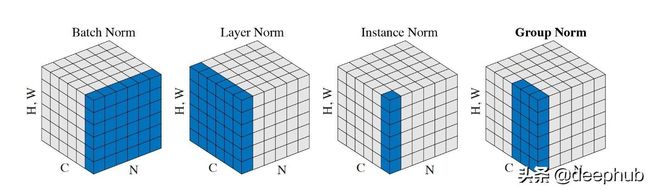
不同的归一化方法
为了促进GN的表述,我们将首先看一下以前的一些标准化方法。
xᵢ ← (xᵢ - ᵢ) / √(ᵢ² + )
对于每个系数xᵢ输入特性。ᵢ和ᵢ²的均值和方差计算的集合Sᵢ系数,和是一个小的常数数值稳定,避免除零。唯一的区别是集Sᵢ是如何选择的。
为说明归一化方法的计算,我们考虑一批N = 3,输入特征a, b, c,它们有通道c = 4,高度H = 1,宽度W = 2:
a = [ [[2, 3]], [[5, 7]], [[11, 13]], [[17, 19]] ]b = [ [[0, 1]], [[1, 2]], [[3, 5]], [[8, 13]] ]c = [ [[1, 2]], [[3, 4]], [[5, 6]], [[7, 8]] ]
因此批将形状(N、C, H, W) =(3、4、1、2)。我们把= 0.00001。
Batch Normalization
BN规范化的渠道和计算ᵢ和ᵢ沿轴(N、H、W)。批次ᵢ系数被定义为一组的批处理xᵢ相同的频道。
第一系数的ᵢ= 2,i=(0,0,0),相应的ᵢ和ᵢ²系数的计算,b和c的第一个频道:
ᵢ = mean(2, 3, 0, 1, 1, 2) = 1.5ᵢ² = var(2, 3, 0, 1, 1, 2) = 0.917
代入归一化公式,
aᵢ ← (2 - 1.5) / √(0.917 + 0.00001) = 0.522
计算a的所有系数
a ← [ [[0.522, 1.567]], [[0.676, 1.690]], [[1.071, 1.630]], [[1.066, 1.492]] ]
Layer Normalization
层归一化(LN)的设计是为了克服BN的缺点,包括它对批大小的限制。计算ᵢ和ᵢ沿着(C、H、W)轴,和Sᵢ定义为所有系数xᵢ属于相同的输入特性。因此,一个输入特征的计算完全独立于批处理中的其他输入特征。
所有的系数是由相同的归一化ᵢ和ᵢ²
ᵢ = mean(2, 3, 5, 7, 11, 13, 17, 19) = 9.625ᵢ² = var(2, 3, 5, 7, 11, 13, 17, 19) = 35.734
计算a的所有系数
a ← [ [[-1.276, -1.108]], [[-0.773, -0.439]], [[0.230, 0.565]], [[1.234, 1.568]] ]
Instance Normalization
实例规范化(IN)可以看作是将BN公式单独应用到每个输入特性(又称实例),就好像它是批处理中的唯一成员一样。更准确地说,在计算ᵢ和ᵢ沿轴(H, W)和Sᵢ的系数被定义为一组相同的输入特性和xᵢ也在同一个频道。
由于IN的计算与批大小为1时BN的计算相同,在大多数情况下,IN实际上会使情况变得更糟。而对于样式转换任务,IN在丢弃图像对比度信息方面优于BN。
第一系数aᵢ= 2,i=i(0,0,0),相应的ᵢ和ᵢ²只是
ᵢ = mean(2, 3) = 2.5ᵢ² = var(2, 3) = 0.25
当
aᵢ ← (2 - 2.5) / √(0.25 + 0.00001) = -1.000
得到
a ← [ [[-1.000, 1.000]], [[-1.000, 1.000]], [[-1.000, 1.000]], [[-1.000, 1.000]] ]
Group Normalization
前面我们说过IN的计算与批大小为1时BN的计算相同,但是是针对对每个输入特性分别应用BN。注意,IN还可以看作是将LN单独应用于每个通道,就像通道的数量为1的LN一样。
组归一化(GN)是IN和LN的中间点。组织渠道分成不同的组,计算ᵢ和ᵢ沿着(H, W)轴和一组通道。批次ᵢ然后组系数,在相同的输入特性和同一组xᵢ渠道。
组的数量G是一个预定义的超参数,通常需要它来划分c。为了简单起见,我们将通道按顺序分组。所以频道1,…,C / G属于第一组,频道C / G + 1,…,2C / G属于第二组,以此类推。当G = C时,即每组只有1个信道,则GN变为IN。另一方面,当G = 1时,GN变成LN。因此G控制了IN和LN之间的差值。
在我们的例子中,考虑G = 2。规范化的第一个系数aᵢ = 2,i=(0,0,0),我们使用的系数在4 / 2 = 2通道
ᵢ = mean(2, 3, 5, 7) = 4.25ᵢ² = var(2, 3, 5, 7) = 3.687
代入归一化公式,
aᵢ ← (2 - 4.25) / √(3.687 + 0.00001) = -1.172
对于a的其他系数,计算方法相似:
a ← [ [[-1.172, -0.651]], [[0.391, 1.432]], [[-1.265, -0.633]], [[0.633, 1.265]] ]
归一化方法比较
蓝色的区域对应的集Sᵢ计算ᵢ和ᵢ,然后用来正常化任何系数在蓝色区域。
从这个图中我们可以看到,GN如何在IN和LN之间插入。GN优于IN,因为GN可以利用跨渠道的依赖关系。它也比LN好,因为它允许对每一组通道学习不同的分布。
当批大小较小时,GN始终优于BN。但是,当批处理大小非常大时,GN的伸缩性不如BN,可能无法匹配BN的性能。
引用
1. A. Kolesnikov, L. Beyer, X. Zhai, J. Puigcerver, J. Yung, S. Gelly, and N. Houlsby. Big Transfer (BiT): General Visual Representation Learning (2019), arXiv preprint.
1. S. Qiao, H. Wang, C. Liu, W. Shen, and A. Yuille. Weight Standardization (2019), arXiv preprint.
1. S. Santurkar, D. Tsipras, A. Ilyas, and A. Madry. How Does Batch Normalization Help Optimization? (2018), NIPS 2018.
1. Y. Wu, and K. He. Group Normalization (2018), ECCV 2018.
作者:Wanshun Wong
Deephub翻译组