机器学习实战：利用随机森林回归树来预测不同经纬度的无线电电磁波

学习笔记，仅供参考！

介绍

Scikit-learn（以前称为scikits.learn，也称为sklearn）是一款免费的机器学习库 。它具有各种分类，回归和聚类算法，包括支持向量机，随机森林，梯度提升，k均值和DBSCAN，本文利用sklearn的RandomForestRegressor模型对无线电电磁波场强做数据预测。

数据集

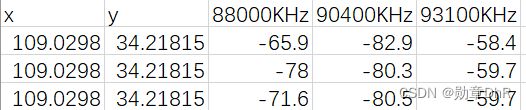
给出如下图数据示例，这是一个在不同经纬度下的无线电场强数据，X，Y表示经纬度，在这么一个物理地址上去发射88M的无线电电磁波，88000khz表示无线电电磁波，再从原地做一个接收，发现场强衰减了65.9khz，衰减表示可能被周边环境的值所吸收，现在根据已有的数据集，来对不同的场强做预测。

代码

完整代码在最后，这里对各行代码进行注释，便于理解。

1.由于给出的数据集的x，y值存在相同的情况，需要先对相同的x，y数据进行求和再娶均值，利用pandas里面封装的groupby函数和mean函数进行同类数据求和再取均值：

	#读入数据
    data_prime = pd.read_csv('FieldIntensity.csv', header=0)
    data_group = data_prime.groupby(by=['x', 'y'])  
    data_mean = data_group.mean()
    data = data_mean.reset_index()
    

2.将经纬度数据作为输入x，场强作为输出y，这里选择对93.1M场强来做预测，将数据集随机打乱，再做切分，3/4作为训练集，1/4作为测试集，这里不是一个分类问题，数据有渐变性，用随机森林回归树来训练模型：

RandomForestRegressor函数参数，参考下面地址：
https://wenku.baidu.com/view/edda0dc9fbc75fbfc77da26925c52cc58bd690bf.html

x = data[['x', 'y']]
    y = data['93100KHz']
    # 切分训练集和测试集，训练集占75%，random_state 相当于随机数种子random.seed() ，其作用是相同的
    x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.75, random_state=0)
    # 随机森林回归决策树，树的个数100，选择节点criterion=mse，mae，数的深度14，每个节点的最少样本数3
    model = RandomForestRegressor(n_estimators=100, criterion='squared_error', max_depth=14, min_samples_split=3)
    model.fit(x_train.values, y_train)
    

3.对训练集和测试集做预测，这里先对数据进行了排序，再利用hstack函数对数据在水平方向做堆叠，方便可视化分析结果，易于观看

# 对训练集进行一个排序，目的是使得可视化结果更明白
    order = y_train.argsort(axis=0)  # argsort函数按index每个数据的下标进行排序
    y_train = y_train.values[order]
    x_train = x_train.values[order, :]
    # 训练预测值
    y_train_pred = model.predict(x_train)
    # 测试集
    order = y_test.argsort(axis=0)
    y_test = y_test.values[order]
    x_test = x_test.values[order, :]
    # 测试预测值
    y_test_pred = model.predict(x_test)
    # 按水平方向将x_test, y_test,y_test_pred进行堆叠
    data = np.hstack((x_test, y_test.reshape(-1, 1), y_test_pred.reshape(-1, 1)))
    # 存入DataFrame
    data = pd.DataFrame(data, columns=['X', 'Y', '931M', '931M_pred'])
    # 排序，原地升序
    data.sort_values('931M', inplace=True, ascending=True)
    pd.set_option('display.min_rows', 10)  # 数据显示10行
    print(data)

4.对训练数据进行评估，回归模型的性能的评价指标主要有：RMSE(平方根误差)、MAE（平均绝对误差）、MSE(平均平方误差)、R2_score（决定系数），这里分别使用了上面四种回归模型评估方法：

 # 训练集
    mae_train = mean_absolute_error(y_train, y_train_pred)  # 对真实值和预测值的误差取绝对值，在求均值
    mse_train = mean_squared_error(y_train, y_train_pred)  # 对真实值和预测值的误差取平方，在求均值
    rmse_train = np.sqrt(mse_train)  # 对真实值和预测值的误差取平方跟，在求均值
    r2_train = r2_score(y_train, y_train_pred)  # 决定系数，反映因变量的全部变异能通过回归关系被自变量解释的比例
    # 测试集
    mae_test = mean_absolute_error(y_test, y_test_pred)
    mse_test = mean_squared_error(y_test, y_test_pred)
    rmse_test = np.sqrt(mse_test)
    r2_test = r2_score(y_test, y_test_pred)
    print('训练集：MSE=%.3f,RMSE=%.3f,MAE=%.3f,R2=%.6f' % (mse_train, rmse_train, mae_train, r2_train))
    print('测试集：MSE=%.3f, RMSE=%.3f, MAE=%.3f, R2=%.6f' % (mse_test, rmse_test, mae_test, r2_test))

    mpl.rcParams['font.sans-serif'] = ['simHei']
    mpl.rcParams['axes.unicode_minus'] = False  # 显示中文的label
    show_data(y_train, y_train_pred, '训练数据误差')
    show_data(y_test, y_test_pred, '测试数据误差')
    plt.show()

5.上面调用了show_data函数，主要是用来做数据可视化：

def show_data(y, y_pred, title):
    plt.figure(figsize=(7, 6), facecolor='w')
    plt.plot(y, 'r-', lw=2, label='真实值')  # y的颜色r，用线表示
    plt.plot(y_pred, 'bo', ms=1, label='预测值', alpha=0.7)  # 颜色b,用点
    plt.grid(linestyle=':', color='#B0B0B0')  # 背景图
    plt.xlabel('采样点', fontsize=15)
    plt.ylabel('场强', fontsize=15)
    plt.legend(loc='upper left')
    plt.title(title, fontsize=18)
    plt.tight_layout()

实验结果

对数据结果分析，X，Y（经纬度），93.1Mkh（无线电场强），93.1M_pred（预测值），从10行数据里可以看到预测结果和真实值基本符合，在训练集和测试集差距不大

               X          Y       93.1M  93.1M_pred
0     109.143619  34.197953 -101.666667  -73.650457
1     109.171567  34.136550  -92.939474  -90.463649
2     109.170186  34.135658  -92.313889  -89.021525
3     109.173731  34.135869  -91.321429  -92.211941
4     109.174453  34.135136  -90.995238  -86.646649
...          ...        ...         ...         ...
1207  109.066967  34.241164  -39.135135  -41.050157
1208  109.066181  34.239458  -38.904878  -37.051476
1209  109.065778  34.238858  -38.678947  -38.104937
1210  109.073261  34.235228  -38.450000  -39.847257
1211  109.092494  34.218008  -37.770000  -42.547054

[1212 rows x 4 columns]
训练集：MSE=0.885,RMSE=0.941,MAE=0.687,R2=0.991823
测试集：MSE=4.273, RMSE=2.067, MAE=1.415, R2=0.961634

数据可视化结果：

全部代码如下：

# 随机森林回归预测场强

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.metrics import r2_score, mean_absolute_error, mean_squared_error


def show_data(y, y_pred, title):
    plt.figure(figsize=(7, 6), facecolor='w')
    plt.plot(y, 'r-', lw=2, label='真实值')  # y的颜色r，用线表示
    plt.plot(y_pred, 'bo', ms=1, label='预测值', alpha=0.7)  # 颜色b,用点
    plt.grid(linestyle=':', color='#B0B0B0')  # 背景图
    plt.xlabel('采样点', fontsize=15)
    plt.ylabel('场强', fontsize=15)
    plt.legend(loc='upper left')
    plt.title(title, fontsize=18)
    plt.tight_layout()


if __name__ == '__main__':
    data_prime = pd.read_csv('FieldIntensity.csv', header=0)
    print(type(data_prime))
    data_group = data_prime.groupby(by=['x', 'y'])  # 对相同的x，y做求和再取均值
    print(type(data_group))
    data_mean = data_group.mean()
    print(data_mean)
    data = data_mean.reset_index()
    print(data)

    #对93100khz进行预测
    x = data[['x', 'y']]
    y = data['93100KHz']
    # 切分训练集和测试集，训练集占75%，random_state 相当于随机数种子random.seed() ，其作用是相同的
    x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.75, random_state=0)
    # 随机森林回归决策树，树的个数100，选择节点criterion=mse，mae，数的深度14，每个节点的最少样本数3
    model = RandomForestRegressor(n_estimators=100, criterion='squared_error', max_depth=14, min_samples_split=3)
    model.fit(x_train.values, y_train)

    # 对训练集进行一个排序，目的是使得可视化结果更明白
    order = y_train.argsort(axis=0)  # argsort函数按index每个数据的下标进行排序
    y_train = y_train.values[order]
    x_train = x_train.values[order, :]
    # 训练预测值
    y_train_pred = model.predict(x_train)
    # 测试集
    order = y_test.argsort(axis=0)
    y_test = y_test.values[order]
    x_test = x_test.values[order, :]
    # 测试预测值
    y_test_pred = model.predict(x_test)

    # 按水平方向将x_test, y_test,y_test_pred进行堆叠
    data = np.hstack((x_test, y_test.reshape(-1, 1), y_test_pred.reshape(-1, 1)))
    # 存入DataFrame
    data = pd.DataFrame(data, columns=['X', 'Y', '93.1M', '93.1M_pred'])
    # 排序，原地升序
    data.sort_values('93.1M', inplace=True, ascending=True)
    pd.set_option('display.min_rows', 10)  # 数据显示10行
    print(data)

    # 训练集
    mae_train = mean_absolute_error(y_train, y_train_pred)  # 对真实值和预测值的误差取绝对值，在求均值
    mse_train = mean_squared_error(y_train, y_train_pred)  # 对真实值和预测值的误差取平方，在求均值
    rmse_train = np.sqrt(mse_train)  # 对真实值和预测值的误差取平方跟，在求均值
    r2_train = r2_score(y_train, y_train_pred)  # 决定系数，反映因变量的全部变异能通过回归关系被自变量解释的比例
    # 测试集
    mae_test = mean_absolute_error(y_test, y_test_pred)
    mse_test = mean_squared_error(y_test, y_test_pred)
    rmse_test = np.sqrt(mse_test)
    r2_test = r2_score(y_test, y_test_pred)
    print('训练集：MSE=%.3f,RMSE=%.3f,MAE=%.3f,R2=%.6f' % (mse_train, rmse_train, mae_train, r2_train))
    print('测试集：MSE=%.3f, RMSE=%.3f, MAE=%.3f, R2=%.6f' % (mse_test, rmse_test, mae_test, r2_test))

    mpl.rcParams['font.sans-serif'] = ['simHei']
    mpl.rcParams['axes.unicode_minus'] = False  # 显示中文的label
    show_data(y_train, y_train_pred, '训练数据误差')
    show_data(y_test, y_test_pred, '测试数据误差')
    plt.show()

数据集自取：
链接：https://pan.baidu.com/s/1_qDBvq1LIne0e5zClhB7QQ
提取码：auht