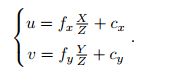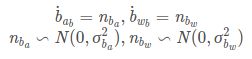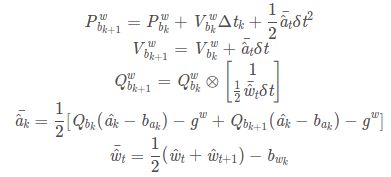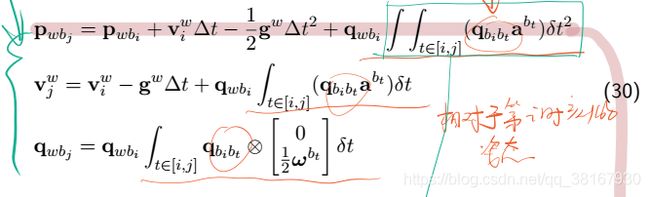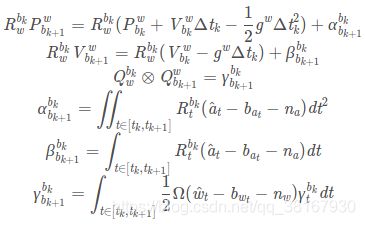VINS-Mono学习（一）——数据预处理
void push_back(double dt, const Eigen::Vector3d &acc, const Eigen::Vector3d &gyr)
{
dt_buf.push_back(dt);
acc_buf.push_back(acc);
gyr_buf.push_back(gyr);
propagate(dt, acc, gyr);
}将VINS-Mono按照如下框架划分为5部分：
即：
- 数据预处理
- 松耦合初始化提供优化初值和状态
- 基于滑动窗口的VIO紧耦合后端非线性优化
- 闭环检测
- 闭环优化（4DoF）
需要注意的是，VINS中开启了4个线程，分别是：
- 前端图像跟踪
- 后端非线性优化
- 闭环检测
- 闭环优化
目录
0、VINS常见面试题汇总
0.1 说一下VINS-Mono的优缺点
0.2 推导一下VINS-Mono里面的预积分公式
0.3 如何标定IMU与相机之间的外参数？
0.4 Vins-Mono里面什么是边缘化？First Estimate Jacobian？一致性？可观性？
1、VINS鲁棒初始化
2、VINS前端知识汇总
2.1 前端流程概述
2.1.1 createCLAHE()自适应局部直方图均衡化
2.1.2 calcOpticalFlowPyrLK()光流追踪
2.1.3 rejectWithF()
2.1.4 setMask()
2.1.5 goodFeaturesToTrack()特征点提取
2.1.6 前端发布出去的消息类型
2.2 关键帧相关
3、VINS预积分和后端优化IMU部分
4、VINS 边缘化marginalization理论和代码详解
5、回环检测 sim3
参考大佬的博客进行学习：
https://blog.csdn.net/qq_41839222/article/details/87878550
Harris 和 Shi-Tomasi 都是基于梯度计算的角点检测方法，Shi-Tomasi 的效果要好一些。基于梯度的检测方法有一些缺点: 计算复杂度高，图像中的噪声可以阻碍梯度计算。
想要提高检测速度的话，可以考虑基于模板的方法：FAST角点检测算法。该算法原理比较简单，但实时性很强。
VINS-Mono是香港科技大学开源的一个VIO算法，用紧耦合的方法，通过单目+IMU恢复出尺度，效果非常棒。
VINS的功能模块可包括五个部分：数据预处理、初始化、后端非线性优化、闭环检测及闭环优化。代码中主要开启了四个线程，分别是：前端图像跟踪、后端非线性优化（其中初始化和IMU预积分在这个线程中）、闭环检测、闭环优化。
1、图像和IMU预处理
（1）图像：提取图像shi-Tomas角点，金字塔光流跟踪相邻帧，RANSAC去除异常点，最后将跟踪到的特征点push到图像队列中，并通知后端进行处理。
（2）IMU：1）IMU积分，得到PVQ位置、速度、旋转，2）计算在后端优化中将用到的相邻帧的预积分增量，3）计算预积分误差的Jacobian矩阵和协方差。
2、初始化
（1）SFM纯视觉估计滑动窗口内所有帧的位姿和3D路标点的逆深度；
（2）SFM与IMU预积分松耦合，对齐求解初始化参数。
3、后端滑动窗口优化
将视觉约束、IMU约束、先验约束、闭环约束放在一个大的目标函数中进行非线性优化，求解滑动窗口内所有帧的PVQ、Bias。
4、闭环检测和优化
DBow进行闭环检测，检测成功后重定位，最后对整个相机轨迹进行闭环优化。
0、VINS常见面试题汇总
VIO引出原因：
1、单纯视觉：缺点：尺度不确定性，单目旋转无法估计、快速运动易丢失，受图像遮挡物体干扰。优点：不产生漂移，直接测量旋转与平移。
2、单纯IMU：缺点：零偏导致漂移、低精度IMU积分位姿发散。
3、结合视觉+IMU：可用视觉弥补IMU的零偏，
- IMU适合计算短时间、快速的运动
- 视觉适合计算长时间、慢速的运动
- 可利用视觉定位信息来估计IMU的零偏、减少IMU由零偏导致的发散和累计误差
- IMU可以为视觉提供快速运动时的定位
VINS贡献：
1、一个紧耦合、基于优化的单目视觉惯性里程计，具有相机-IMU外部校准和IMU偏置估计。
2、基于有界滑动窗口迭代进行估计。
3、基于滑动窗口里的关键帧维持视觉结构，基于关键帧之间的IMU进行预积分维持惯性测量。
4、鲁棒性：未知状态的初始化、相机和IMU外参数的在线标定、球面不同意重投影误差、回环检测、四自由度位姿图优化（三位置和航向）。
0.1 说一下VINS-Mono的优缺点
（1）VINS-Mono的前端是采用提取关键点然后采用光流法追踪，因此对于弱纹理，关键点少的环境鲁棒性和精度差；
（2）同样还是前端的问题，因为没有提取特征描述子，而是使用光流法进行追踪匹配，一旦画面模糊或者图像丢失，相机就会丢，而且没有重定位模块。
（3）在恒速运动下，会使得IMU有一个自由度不可观，因此会发生漂移。
0.2 推导一下VINS-Mono里面的预积分公式
0.3 如何标定IMU与相机之间的外参数？
0.4 Vins-Mono里面什么是边缘化？First Estimate Jacobian？一致性？可观性？
边缘化其实简单说就是将滑窗中丢弃的图像帧的信息保留下来传递给剩余变量的方式。
First Estimate Jacobian是为了解决新测量信息和旧的先验信息构建新的系统时，对某一优化变量求雅可比的线性化点不同导致信息矩阵的零空间发生变化，不可观的变量变成可观变量的问题，做法就是保证变量的线性化点不变。
一致性应该值得是就是线性化点的一致不变，而可观性的定义和现代控制理论中能观性定义是一致的，即通过测量获得状态变量的信息，即该变量是能观的。
这里给出深蓝学院课件中给定的一种定义：
对于测量系统
，其中
为测量值，θ∈
为系统状态量，
为测量噪声问题。
是个非线性函数，将状态量映射成测量。对于理想数据，如果以下条件成立，则系统状态量θ可观：
1、VINS鲁棒初始化
2、VINS前端知识汇总
VINS-Mono的前端看上去思路是比较简单的，但是如果仔细阅读源码的话还是能看出许多非常有技术性的东西的，下面我就把一些我觉得很有意思的细节码出来，分享一下。
也可以参见《在代码中分析VINS——图解feature_tracker.cpp》https://blog.csdn.net/liuzheng1/article/details/89406276 看一看点跟踪的具体过程。
2.1 前端流程概述
VINS-Mono的前端整个封装成了一个ROS节点
其订阅的topic是：
- 相机或者数据集发来的图片
其发布topic是：
- 由pub_img发布的"feature"，发布的是当前帧的特征点，特征点分装成了sensor_msgs::PointCloudPtr类型，里面包括了每个特征点的（1）归一化平面上的坐标（2）归一化平面上的速度（3）图像平面上的坐标，这三者中归一化平面坐标是在SFM和后端用到，而归一化平面上的速度以及图像平面上的坐标仅仅在进行时间偏差估计时会用到。
- 由pub_match发布的“feature_img”，发布的是用来调试的带特征点的灰度图，图上特征点的颜色越红代表此特征点被跟踪的帧数越多，越蓝表示越少。
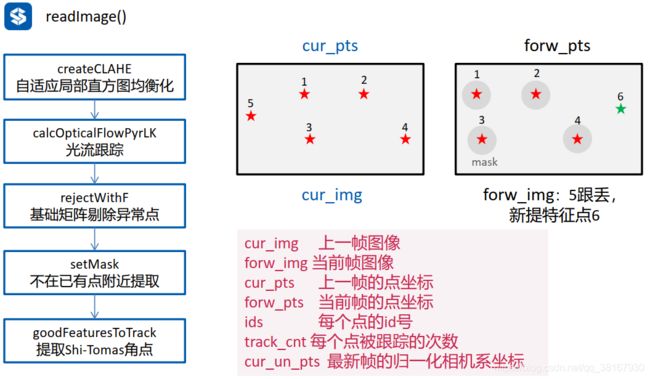
在图片的回调函数中会先对时间进行控制，然后会进入 readImage() 函数 进行光流追踪、特征点提取、特征点提取等步骤。
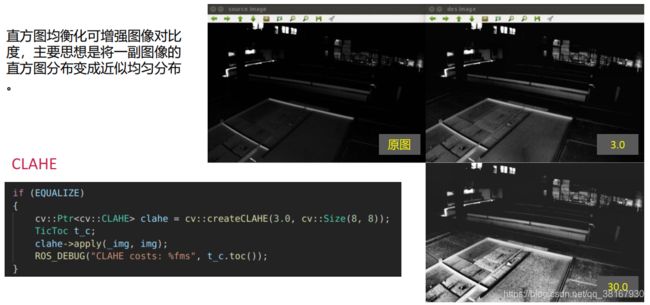
2.1.1 createCLAHE()自适应局部直方图均衡化
createCLAHE()函数是进行自适应局部直方图均衡化。直方图均衡化可增强图像对比度，主要思想是将一副图像的直方图分布变成近似均匀分布。
2.1.2 calcOpticalFlowPyrLK()光流追踪
vector status;
vector err;
cv::calcOpticalFlowPyrLK(cur_img, forw_img, cur_pts, forw_pts, status, err, cv::Size(21,21), 3); 
OpenCV中提供了KLT光流检测算法的APIcalcOpticalFlowPyrLK()。这个API是默认使用图像金字塔的KLT光流检测算法，将每帧图像建立图像金字塔，并自顶向底依次将前后两帧图像的金字塔中的同一层图像进行光流检测，直至检测完所有每一层图像，得到最后的输出。由于自顶向底的金字塔图像其分辨率是从低到高，当目标出现较大的运动时，低分辨率图像中的特征点也不会移动出邻近窗口，仍能被算法检测到。所以使用图像金字塔的KLT算法能够允许目标比较大的运动。其参数含义如下：
第一个参数prevImg：输入的上一帧图像；
第二个参数nextImg：输入的下一帧图像；
第三个参数prevPts：输入的上一帧图像的稀疏特征点集；
第四个参数nextPts：输出的下一帧图像对应的稀疏特征点集；
第五个参数status：输出点的状态向量，可用于判断某特征点在两帧图像之间是否存在光流；如果某点在两帧图像之间存在光流，则status向量中对应该点的元素设置为1，否则设置为0；
第六个参数err：输出错误的向量，向量的每个元素都设置为相应特征点的错误；
第七个参数winsize：搜索窗口大小；
第八个参数maxLevel = 3, 金字塔层数，0表示只检测当前图像，不使用图像金字塔的KLT算法；
第九个参数criteria = TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 30, 0.01), 表示窗口搜索停止条件；
第十个参数int flags = 0, 操作标志；
第十一个参数minEigThreshold = 1e-4 ，最小特征值响应，低于最小值不做处理。
2.1.3 rejectWithF()
上面进行特征跟踪得到当前帧特征点之后，可能会存在误匹配，VINS采用使用RANSAC来计算F矩阵，剔除无匹配点。源码如下，比较简单：
void FeatureTracker::rejectWithF()
{
if (forw_pts.size() >= 8)
{
ROS_DEBUG("FM ransac begins");//才哟ing的是ransac的方法
TicToc t_f;
vector un_cur_pts(cur_pts.size()), un_forw_pts(forw_pts.size());
for (unsigned int i = 0; i < cur_pts.size(); i++)
{
Eigen::Vector3d tmp_p;
//根据不同的相机模型将二维坐标转换到三维坐标
m_camera->liftProjective(Eigen::Vector2d(cur_pts[i].x, cur_pts[i].y), tmp_p);
//转换为归一化像素坐标
tmp_p.x() = FOCAL_LENGTH * tmp_p.x() / tmp_p.z() + COL / 2.0;
tmp_p.y() = FOCAL_LENGTH * tmp_p.y() / tmp_p.z() + ROW / 2.0;
un_cur_pts[i] = cv::Point2f(tmp_p.x(), tmp_p.y());
m_camera->liftProjective(Eigen::Vector2d(forw_pts[i].x, forw_pts[i].y), tmp_p);
tmp_p.x() = FOCAL_LENGTH * tmp_p.x() / tmp_p.z() + COL / 2.0;
tmp_p.y() = FOCAL_LENGTH * tmp_p.y() / tmp_p.z() + ROW / 2.0;
un_forw_pts[i] = cv::Point2f(tmp_p.x(), tmp_p.y());
}
vector status;
//调用cv::findFundamentalMat对un_cur_pts和un_forw_pts计算F矩阵
cv::findFundamentalMat(un_cur_pts, un_forw_pts, cv::FM_RANSAC, F_THRESHOLD, 0.99, status);
int size_a = cur_pts.size();
reduceVector(prev_pts, status);
reduceVector(cur_pts, status);
reduceVector(forw_pts, status);
reduceVector(cur_un_pts, status);
reduceVector(ids, status);
reduceVector(track_cnt, status);
ROS_DEBUG("FM ransac: %d -> %lu: %f", size_a, forw_pts.size(), 1.0 * forw_pts.size() / size_a);
ROS_DEBUG("FM ransac costs: %fms", t_f.toc());
}
}
上面转换为归一化像素坐标的公式如下：
这里主要的操作是将图像平面上的特征点，投影到归一化平面上，然后消除畸变，这就是调用liftProjective函数实现的，camera_model功能包通过工厂模式生成了多种相机模型，不同的相机模型的liftProject函数里面的算法不同，但是好像这项相机模型对应的畸变消除算法和《SLAM14讲》中讲的最基本的那种k1、k2、k3、p1、p2五个参数的畸变校正模型不同，具体的相机模型我还没有时间去研究，这里我还是有两个问题：
- 为什么FOCAL_LENGTH在程序中设置成了460这个数值？
- 为什么要将特征带点转化到归一化平面上的像素坐标？
排除这两个问题之外，其他其实也就很简单了，通过findFundamentalMat函数自带的ransac消除外点的功能在光流法之后以及提取新的特征点之前消除光流法更踪错误的点，维持系统精度。
《SLAM14讲》关于畸变校正模型的介绍如下：
2.1.4 setMask()
setMask() 函数主要是和特征点提取有关的，当跟踪的特征点数量没有达到设定的值时就会对图片进行特征点提取，提取采取的算法是OpenCV的Harris角点提取函数：
cv::goodFeaturesToTrack(forw_img, n_pts, MAX_CNT - forw_pts.size(), 0.01, MIN_DIST, mask);函数的最后一个参数mask是是设置角点提取的区域，实际上是和输入forw_img尺寸相同的一个Mat数据类型，而这个mask就在这里就是通过setMask()函数生成的，它的作用是使得提取的特征点分布尽可能均匀，setMask() 函数源码如下：
void FeatureTracker::setMask()
{
if(FISHEYE)
mask = fisheye_mask.clone();
else
mask = cv::Mat(ROW, COL, CV_8UC1, cv::Scalar(255));
//算法会更加倾向于保留跟踪时间长的特征点
vector>> cnt_pts_id;
for (unsigned int i = 0; i < forw_pts.size(); i++)
cnt_pts_id.push_back(make_pair(track_cnt[i], make_pair(forw_pts[i], ids[i])));
//对光流跟踪到的特征点forw_pts，按照被跟踪到的次数cnt从大到小排序
sort(cnt_pts_id.begin(), cnt_pts_id.end(), [](const pair> &a, const pair> &b)
{
return a.first > b.first;
});
//清空cnt，pts，id并重新存入
forw_pts.clear();
ids.clear();
track_cnt.clear();
for (auto &it : cnt_pts_id)
{
if (mask.at(it.second.first) == 255)
{
//当前特征点位置对应的mask值为255，则保留当前特征点，将对应的特征点位置pts，id，被追踪次数cnt分别存入
forw_pts.push_back(it.second.first);
ids.push_back(it.second.second);
track_cnt.push_back(it.first);
//在mask中将当前特征点周围半径为MIN_DIST的区域设置为0，后面不再选取该区域内的点（使跟踪点不集中在一个区域上）
cv::circle(mask, it.second.first, MIN_DIST, 0, -1);
}
}
} 其大概流程是会根据光流法跟踪下一帧图片forw_img获得的forw_pts的被跟踪的时间进行排序，然后按照被跟踪时间从长到段的顺序以半径MIN_DIST在一张白图上画黑圈，如果画出来的mask大概长下面这个样子（有点密集恐惧症了…）：
将这个mask图输入到goodFeaturesToTrack函数中，函数就只会在白色区域，也就是没有跟踪时长特别长的地区提取特征点，因此会使得我们提取的关键点相对较为均匀，如下图所示：
如果你将setMask函数中排序的部分注释掉，特征点的分布就会变成如下图所示结果：
我个人觉得上面这种做法应该是有利有弊的，对于纹理特征丰富的环境，这种操作使得特征点分布更加均匀是有利于系统鲁棒性的，在ORB SLAM2和SVO等经典框架中，前端都有相应的均匀分布的操作，但是在上面图片中这种纹理特征稀疏的环境下，这种做法就不一定好用了，因为强行使得特征点分布到一些本来就没什么特征的区域，这样可能（因为这里我还没有做实验验证）会使得系统精度下降。
2.1.5 goodFeaturesToTrack()特征点提取
特征点在光流追踪过程中会有损失，因此继续使用goodFeaturesToTrack()提取Shi-Tomas角点，补充计算特征点。代码如下：
cv::goodFeatureToTrack(forw_img, n_pts, MAX_CNT - forw_pts.size(), 0.01, MIN_DIST, mask);
2.1.6 前端发布出去的消息类型
2.2 关键帧相关
①需不需要关键帧
②怎么选关键帧
③控制关键帧的数量
④仅在关键帧中补充新特征点？还是对所有关键帧提取新特征点？
⑤何时进行三角化？
3、VINS预积分和后端优化IMU部分
关于VINS-Mono系统的理论推导和代码讲解，网上有很多优秀的博客，如：
- VINS-Mono代码分析与总结(一) IMU预积分；
- VINS-Mono源码解析（三）后端: IMU预积分；
- VINS-Mono预积分公式推导；
- VINS-Mono 论文公式推导与代码解析；
- VINS-Mono代码分析总结VINS-Mono理论学习——IMU预积分 Pre-integration （Jacobian 协方差) VINS论文推导及代码解析 by 崔华坤。
本部分主要参考这些讲解，结合代码和理论推导，对IMU预积分部分进行梳理与总结，对看代码的过程中的一些疑惑进行分析讨论。
3.1 IMU模型
IMU测量值包括加速度计得到的线速度
和陀螺仪得到的角速度
，有：
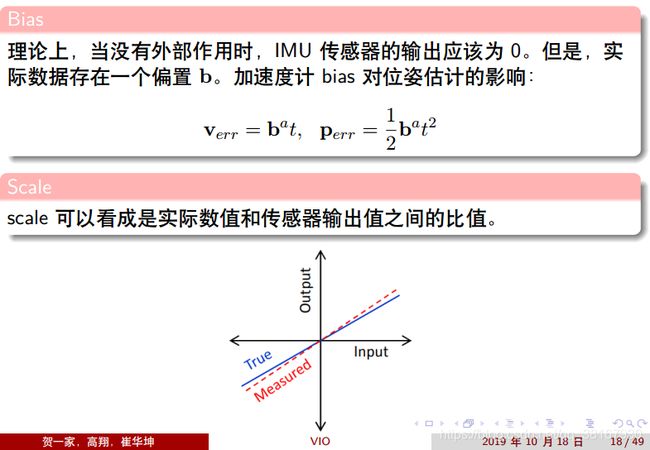
其中，b下标代表body坐标系，IMU测量值受到加速度偏置ba，陀螺仪偏置bw和附加噪声na，nw的影响，线加速度是重力加速度和物体加速度的合矢量。
IMU的误差类型为：
进一步看IMU的确定性误差为：
假设附加噪声为高斯噪声：
说回偏置bias，加速度计偏置和陀螺仪偏置被建模为随机游走，其导数为高斯性的：
对于图像帧k和k+1，体坐标系对应为
，
，位置/速度和方向旋转）状态值PVQ可以根据[
，
]时间间隔的IMU测量值，在世界坐标系下进行传递。
，
为t时刻从本体坐标系到世界坐标系的旋转矩阵，可以看到坐标系的状态PVQ依赖于的状态。如果直接将体坐标系在世界坐标系下的状态作为变量放在非线性优化中，在进行后端优化时会迭代更新，将导致我们需要根据每次迭代后的状态量进行状态传递，即需要重新传递IMU状态值，将会产生很大的计算量。
上式对应基于中值积分的离散形式，如下：
即取k，k+1时刻的角速度和线加速度的测量值均值作为当前时间段内的角速度和加速度，然后进行积分计算求解位姿。这部分实现函数是在：
void Estimator::processIMU()中，我们具体来看实现：
1、初始化。
if (!first_imu)
{
first_imu = true;
acc_0 = linear_acceleration;
gyr_0 = angular_velocity;
}
if (!pre_integrations[frame_count])
{
pre_integrations[frame_count] = new IntegrationBase{acc_0, gyr_0, Bas[frame_count], Bgs[frame_count]};
}2、预积分。开始预积分 ：
pre_integrations[frame_count]->push_back(dt, linear_acceleration, angular_velocity);
//if(solver_flag != NON_LINEAR)
tmp_pre_integration->push_back(dt, linear_acceleration, angular_velocity);linear_acceleration, angular_velocity分别是当前的测量值，上述两个函数执行同样的操作，计算预计分，因为k , k + 1时刻之间有很多IMU数据，每到来一个IMU数据，就会计算并累加一次预计分。
3、存储测量值到buf中。
dt_buf[frame_count].push_back(dt);
linear_acceleration_buf[frame_count].push_back(linear_acceleration);
angular_velocity_buf[frame_count].push_back(angular_velocity);4、基于中值积分对当前位姿进行估计。
int j = frame_count;
Vector3d un_acc_0 = Rs[j] * (acc_0 - Bas[j]) - g;
Vector3d un_gyr = 0.5 * (gyr_0 + angular_velocity) - Bgs[j];
Rs[j] *= Utility::deltaQ(un_gyr * dt).toRotationMatrix();
Vector3d un_acc_1 = Rs[j] * (linear_acceleration - Bas[j]) - g;
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);
Ps[j] += dt * Vs[j] + 0.5 * dt * dt * un_acc;
Vs[j] += dt * un_acc;其中，acc_0，gyr_0是上一时刻的测量值，代码分别与前述中值积分的公式相对应。这里所得到的位姿估计是用于后面作为非线性优化的初始值。
后面会介绍如何使用IMU构建的测量值作为观测，对两时刻之间的状态量进行约束，也即如何通过预积分构建IMU的预积分残差。
3.2 IMU预积分
通过简单的公式转换，将世界坐标系下的积分模型转换为bi坐标系下的预积分模型：
那么，PVQ积分公式中的积分项则变成相对于第i时刻的姿态，而不是相对于世界坐标系的姿态：
因此，IMU预积分的连续形式如下：
IMU预积分的离散形式如下：
上面是深蓝学院的课件，我们再来看看崔神的解释：
IMU预积分的思想是将参考坐标系从世界坐标系调整到第k帧的体坐标系bk，即同时乘以
。
此时的积分结果
可以理解为bk+1对bk的相对运动量，bk的状态改变并不会对其产生影响，因此将其视作非线性优化残差中的测量值，可以避免状态的重复传递。下面对其离散形式进行介绍：
代码中基于中值积分对 
进行计算，在：
IntergrationBase::push_back()中实现，对应的计算公式为：
初始状态
为0，
为单位四元数，na，nw被视为0.
所对应的代码为：
void push_back(double dt, const Eigen::Vector3d &acc, const Eigen::Vector3d &gyr)
{
dt_buf.push_back(dt);
acc_buf.push_back(acc);
gyr_buf.push_back(gyr);
propagate(dt, acc, gyr);
}中值积分包含在：
void propagate(double _dt, const Eigen::Vector3d& _acc_1, const Eigen::Vector3d& _gyr_1)
{
dt = _dt; // k+1时刻值
acc_1 = _acc_1; // k+1时刻值
gyr_1 = _gyr_1; // k+1时刻值
Vector3d result_delta_p;
Quaterniond result_delta_q;
Vector3d result_delta_v;
Vector3d result_linearized_ba;
Vector3d result_linearized_bg;
// 预积分的离散形式使用的是中值积分更新
midPointIntegration(_dt, acc_0, gyr_0, _acc_1, _gyr_1, delta_p, delta_q, delta_v,
linearized_ba, linearized_bg,
result_delta_p, result_delta_q, result_delta_v,
result_linearized_ba, result_linearized_bg, 1);
//checkJacobian(_dt, acc_0, gyr_0, acc_1, gyr_1, delta_p, delta_q, delta_v,
// linearized_ba, linearized_bg);
delta_p = result_delta_p;
delta_q = result_delta_q;
delta_v = result_delta_v;
linearized_ba = result_linearized_ba;
linearized_bg = result_linearized_bg;
delta_q.normalize();
sum_dt += dt;
acc_0 = acc_1;
gyr_0 = gyr_1;
}下面是中值积分的函数。首先，按照公式进行积分计算：
void midPointIntegration(double _dt,
const Eigen::Vector3d &_acc_0, const Eigen::Vector3d &_gyr_0,
const Eigen::Vector3d &_acc_1, const Eigen::Vector3d &_gyr_1,
const Eigen::Vector3d &delta_p, const Eigen::Quaterniond &delta_q, const Eigen::Vector3d &delta_v,
const Eigen::Vector3d &linearized_ba, const Eigen::Vector3d &linearized_bg,
Eigen::Vector3d &result_delta_p, Eigen::Quaterniond &result_delta_q, Eigen::Vector3d &result_delta_v,
Eigen::Vector3d &result_linearized_ba, Eigen::Vector3d &result_linearized_bg, bool update_jacobian)
{
//ROS_INFO("midpoint integration");
Vector3d un_acc_0 = delta_q * (_acc_0 - linearized_ba);
Vector3d un_gyr = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg;
result_delta_q = delta_q * Quaterniond(1, un_gyr(0) * _dt / 2, un_gyr(1) * _dt / 2, un_gyr(2) * _dt / 2);
Vector3d un_acc_1 = result_delta_q * (_acc_1 - linearized_ba);
Vector3d un_acc = 0.5 * (un_acc_0 + un_acc_1);
result_delta_p = delta_p + delta_v * _dt + 0.5 * un_acc * _dt * _dt;
result_delta_v = delta_v + un_acc * _dt;
result_linearized_ba = linearized_ba;
result_linearized_bg = linearized_bg;
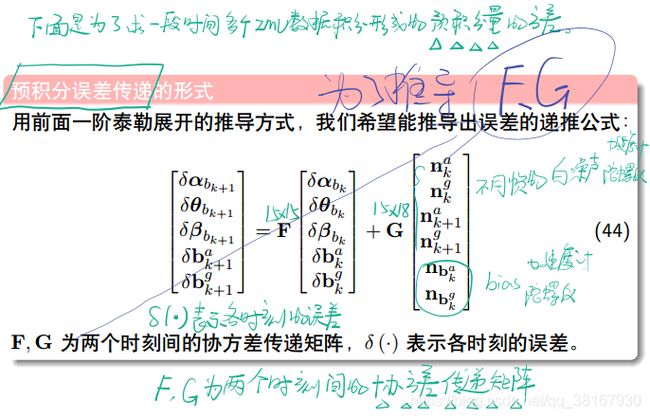
接下来就是更新误差传递的协方差矩阵：
其中F和G的形式如下：
// 随后更新方差矩阵及雅克比
if(update_jacobian)
{
Vector3d w_x = 0.5 * (_gyr_0 + _gyr_1) - linearized_bg; // 角速度的中值w
Vector3d a_0_x = _acc_0 - linearized_ba;
Vector3d a_1_x = _acc_1 - linearized_ba;
Matrix3d R_w_x, R_a_0_x, R_a_1_x;
R_w_x << 0, -w_x(2), w_x(1),
w_x(2), 0, -w_x(0),
-w_x(1), w_x(0), 0;
R_a_0_x << 0, -a_0_x(2), a_0_x(1),
a_0_x(2), 0, -a_0_x(0),
-a_0_x(1), a_0_x(0), 0;
R_a_1_x << 0, -a_1_x(2), a_1_x(1),
a_1_x(2), 0, -a_1_x(0),
-a_1_x(1), a_1_x(0), 0;
// IMU 误差传递 采用 基于误差随时间变化的递推公式 F = I+A△t， G = B△t
// 误差的传递由两部分组成：当前时刻的误差传递给下一时刻 + 当前时刻测量噪声传递给下一时刻。
MatrixXd F = MatrixXd::Zero(15, 15);
F.block<3, 3>(0, 0) = Matrix3d::Identity(); // ①
F.block<3, 3>(0, 3) = -0.25 * delta_q.toRotationMatrix() * R_a_0_x * _dt * _dt +
-0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt * _dt; // ②
F.block<3, 3>(0, 6) = MatrixXd::Identity(3,3) * _dt; // ③
F.block<3, 3>(0, 9) = -0.25 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt * _dt; // ④
F.block<3, 3>(0, 12) = -0.25 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * -_dt; // ⑤
F.block<3, 3>(3, 3) = Matrix3d::Identity() - R_w_x * _dt;
F.block<3, 3>(3, 12) = -1.0 * MatrixXd::Identity(3,3) * _dt;
F.block<3, 3>(6, 3) = -0.5 * delta_q.toRotationMatrix() * R_a_0_x * _dt +
-0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * (Matrix3d::Identity() - R_w_x * _dt) * _dt;
F.block<3, 3>(6, 6) = Matrix3d::Identity();
F.block<3, 3>(6, 9) = -0.5 * (delta_q.toRotationMatrix() + result_delta_q.toRotationMatrix()) * _dt;
F.block<3, 3>(6, 12) = -0.5 * result_delta_q.toRotationMatrix() * R_a_1_x * _dt * -_dt;
F.block<3, 3>(9, 9) = Matrix3d::Identity();
F.block<3, 3>(12, 12) = Matrix3d::Identity();
//cout<<"A"<(0, 0) = 0.25 * delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 3) = 0.25 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * _dt * 0.5 * _dt;
V.block<3, 3>(0, 6) = 0.25 * result_delta_q.toRotationMatrix() * _dt * _dt;
V.block<3, 3>(0, 9) = V.block<3, 3>(0, 3);
V.block<3, 3>(3, 3) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(3, 9) = 0.5 * MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(6, 0) = 0.5 * delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 3) = 0.5 * -result_delta_q.toRotationMatrix() * R_a_1_x * _dt * 0.5 * _dt;
V.block<3, 3>(6, 6) = 0.5 * result_delta_q.toRotationMatrix() * _dt;
V.block<3, 3>(6, 9) = V.block<3, 3>(6, 3);
V.block<3, 3>(9, 12) = MatrixXd::Identity(3,3) * _dt;
V.block<3, 3>(12, 15) = MatrixXd::Identity(3,3) * _dt;
//step_jacobian = F;
//step_V = V;
jacobian = F * jacobian;
covariance = F * covariance * F.transpose() + V * noise * V.transpose();
} 3.3 IMU预积分残差计算
预积分所形成的约束边，在integration_base.h文件中的最后一个函数evaluate()函数会计算给定相邻帧和状态量的残差：
// 计算和给定相邻帧状态量的残差
Eigen::Matrix evaluate(const Eigen::Vector3d &Pi, const Eigen::Quaterniond &Qi, const Eigen::Vector3d &Vi, const Eigen::Vector3d &Bai, const Eigen::Vector3d &Bgi,
const Eigen::Vector3d &Pj, const Eigen::Quaterniond &Qj, const Eigen::Vector3d &Vj, const Eigen::Vector3d &Baj, const Eigen::Vector3d &Bgj)
{
Eigen::Matrix residuals;
Eigen::Matrix3d dp_dba = jacobian.block<3, 3>(O_P, O_BA);
Eigen::Matrix3d dp_dbg = jacobian.block<3, 3>(O_P, O_BG);
Eigen::Matrix3d dq_dbg = jacobian.block<3, 3>(O_R, O_BG);
Eigen::Matrix3d dv_dba = jacobian.block<3, 3>(O_V, O_BA);
Eigen::Matrix3d dv_dbg = jacobian.block<3, 3>(O_V, O_BG);
Eigen::Vector3d dba = Bai - linearized_ba;
Eigen::Vector3d dbg = Bgi - linearized_bg;
// 三个预积分量 《VIO》第3讲，公式（77）
Eigen::Quaterniond corrected_delta_q = delta_q * Utility::deltaQ(dq_dbg * dbg); // 旋转 q_bi_bj
Eigen::Vector3d corrected_delta_v = delta_v + dv_dba * dba + dv_dbg * dbg; // 速度 β_bi_bj
Eigen::Vector3d corrected_delta_p = delta_p + dp_dba * dba + dp_dbg * dbg; // 位姿 α_bi_bj
// 《VIO第3讲》 P69页 残差公式 e_B(xi, xj)
residuals.block<3, 1>(O_P, 0) = Qi.inverse() * (0.5 * G * sum_dt * sum_dt + Pj - Pi - Vi * sum_dt) - corrected_delta_p;
residuals.block<3, 1>(O_R, 0) = 2 * (corrected_delta_q.inverse() * (Qi.inverse() * Qj)).vec();
residuals.block<3, 1>(O_V, 0) = Qi.inverse() * (G * sum_dt + Vj - Vi) - corrected_delta_v;
residuals.block<3, 1>(O_BA, 0) = Baj - Bai;
residuals.block<3, 1>(O_BG, 0) = Bgj - Bgi;
return residuals;
} 上面的三个预积分量如下，直接在i时刻的bias附近用一阶泰勒展开来近似：
IMU误差相对于优化变量的Jacobian为：
4、VINS 边缘化marginalization理论和代码详解
4.1 滑动窗口算法
基于边际概率的滑动窗口算法
4.2 滑动窗口中的FEJ算法
5、回环检测 sim3
见文章https://blog.csdn.net/qq_38167930/article/details/119139500 《VINS-Mono学习——回环检测与重定位》
参考文章：
1、https://blog.csdn.net/weixin_44580210/article/details/94355964 VINS-Mono关键知识点总结——前端详解
2、