算法设计与分析第五章贪心算法（一）

算法设计与分析第五章贪心算法（一）

一、贪心算法概述

1、贪心算法总是作出在当前看来最好的选择。
2、贪心算法与动态规划算法的比较
这两种算法都是选择性算法，就是从一个候选集合中选择适当的元素加入解集合。
共同点：
最优子结构性质是选择类最优解都具有的性质，即全优一定包含局优
不同之处：
贪心算法具有贪心选择特性。贪心算法求得局部最优解（局部最优，不一定是全局最优）

二、贪心算法的例题

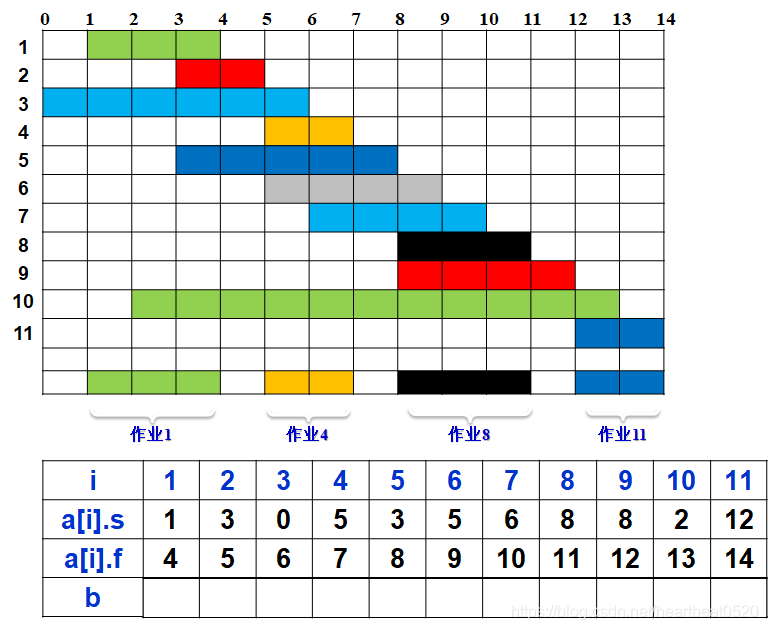
问题一： 活动安排问题

问题描述：
设有n个活动的集合E＝{1，2，…，n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。
每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi，且si＜fi。如果选择了活动i，则它在半开时间区间[si ，fi )内占用资源。若区间[si ，fi )与区间[sj，fj )不相交，则称活动i与活动j是相容的。当 si ≥ fj 或 sj ≥ fi 时，活动i与活动j相容。
活动安排问题就是在所给的活动集合中选出最大的相容活动子集合。
问题分析：
需要根据活动的结束时间对活动进行排序
在排序的基础上，依次来寻找相容的活动

代码：

在这里插入代码片

运行结果：

问题二： 贪心算法 背包问题

问题描述：
给定一个载重量为M的背包，考虑n个物品，其中第i个物品的重量 wi ，价值vi （1≤i≤n），要求把物品装满背包，且使背包内的物品价值最大。
有两类背包问题（根据物品是否可以分割），如果物品不可以分割，称为0-1背包问题（动态规划）；如果物品可以分割，则称为背包问题（贪心算法）。

问题分析：
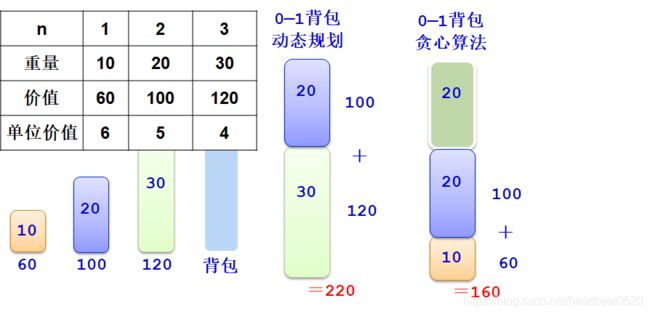
有3种方法来选取物品：
（1）当作0-1背包问题，用动态规划算法，获得最优值220；
（2）当作0-1背包问题，用贪心算法，按性价比从高到底顺序选取物品，获得最优值160。由于物品不可分割，剩下的空间白白浪费。
（3）当作背包问题，用贪心算法，按性价比从高到底的顺序选取物品，获得最优值240。由于物品可以分割，剩下的空间装入物品3的一部分，而获得了更好的性能。

数据结构：

struct bag{
int w; //物品的重量
int v; //物品的价值
double c; //单位重量的价值，v/w
}a[1001]; //存放物品的数组
排序因子（按性价比降序）：
bool cmp(bag a, bag b){
return a.c >= b.c;
}
使用标准模板库函数排序：
sort(a, a+n, cmp);
代码：

#include 
#include 
#include
using namespace std;
#define N 1000
struct bag{
    int w;//物品的重量
    int v;//物品的价值
    double c;//物品的性价比
}a[1001];
bool cmp(bag a,bag b)
{
 return a.c>=b.c;
}

double backpack(int n,bag a[],double c)//n表示物品的数量，a表示按照物品性价比排序后的数组，c表示剩余空间
{
    double cleft=c;
    int i=0;
    double b=0;//获得的价值
    //当物品i可以装入背包中
    while(i<n&&a[i].w<c)
    {
        c=c-a[i].w;
        b+=a[i].v;
        i++;
    }
    //说明物品不能完全装入背包
    if(i<n)
        b+=1.0*a[i].v*c/a[i].w ;
    return b;
}
int main()
{
    int c;
    int n;
    int i;
    printf("请输入背包的容量：\n");
    scanf("%d",&c);
    printf("请输入物品的数量：\n");
    scanf("%d",&n);
    printf("请输入每个物品的重量,价值：\n");
        for(i=0; i<n; i++)
        {
            cin>>a[i].w>>a[i].v;
            a[i].c = 1.0*a[i].v/a[i].w;
        }
        sort(a, a+n, cmp);//按照性价比排序
        printf("输出贪心算法最优解：\n");
        cout<<backpack(n,a,c);
    return 0;
}

运行结果：

问题三：删数问题

问题描述：
给定n位正整数a，去掉其中任意k≤n个数字后，剩下的数字按原次序排列组成一个新的正整数。对于给定的n位正整数a和正整数k，设计一个算法找出剩下数字组成的新数最小的删数方案（顺序不改变）。
输入
第1行是1个正整数a，第2行是正整数k。
输出
对于给定的正整数a，编程计算删去k个数字后得到的最小数

问题分析：
本问题采用贪心算法求解，采用最近下降点优先的贪心策略，即：
x1xi+1,则意味着出现了下降点，
将xi删除。
得到一个n-1位的新数，并且这个新数是所有n-1位数中最小的一个数
从而将问题转换为找最近下降点问题。
代码：

#include 
#include 
using namespace std;
int main(){
	string a; //n位数a
	int k;  //删除数字的个数
	cin>>a>>k;
	if (k >= a.size())  a.erase(); //如果k≥n，所有数字均被删除
	else while(k > 0){	//寻找最近下降点，逐个删除
		int i;
		for (i=0; (i<a.size()-1) && (a[i] <= a[i+1]);  ++i);
		a.erase(i, 1);//删除xi
		k--;
	}
	while(a.size() > 1 && a[0] == '0') 	//删除前导数字0
		a.erase(0, 1);
	cout<<a<<endl;
}

运行结果：

问题四：汽车加油问题

问题描述：
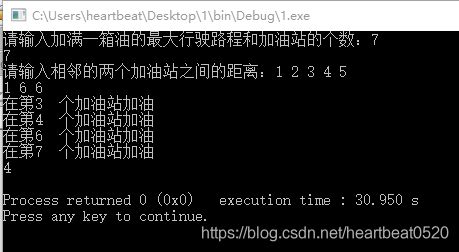
一辆汽车加满油后可行驶n公里。旅途中有若干个加油站。设计一个有效算法，指出应哪些加油站停靠加油，使沿途加油次数最少。对于给定的n(n <= 5000)和k(k <= 1000)个加油站位置，编程计算最少加油次数。要求：
输入：第一行有2个正整数n和k，表示汽车加满油后可行驶n公里，且旅途中有k个加油站。接下来的1行中，有k+1个整数，表示第k个加油站与第k-1个加油站之间的距离。第0个加油站表示出发地，汽车已加满油。第k+1个加油站表示目的地。
输出：输出编程计算出的最少加油次数。如果无法到达目的地，则输出”No Solution”

输入文件示例 输出文件示例
Input.txt output.txt
7 7 4
1 2 3 4 5 1 6 6

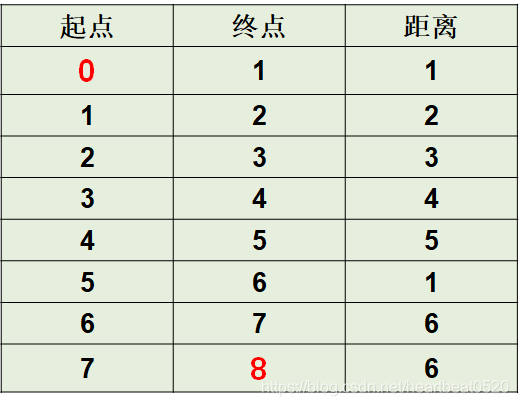
问题分析：
加一次油，跑最远的距离
到达加油站之后，看看剩余的油能否跑到下一个加油站；
能，则不用加油
否则，加油

代码：

#include 
using namespace std;
int main(){
    int n,k,i;
	int *station;
    cout<<"请输入加满一箱油的最大行驶路程和加油站的个数：";
    cin>>n>>k;
    station=new int[k+1];
    cout<<"请输入相邻的两个加油站之间的距离：";
    for(i=0;i<=k;i++)
    cin>>station[i];
    int s=0,number=0;//number记录加油的次数
    s=station[0];//加满油后希望的行驶距离
for(i=1;i<=k;i++)
{    //i代表加油站编号 。1~7.代表将要到大的加油站
		if(s>n)
			{
			    cout<<"No solutin!!";
			break;
				}//判断能否到达i加油站
		else
		{//能到达加油站i
	  	    s=s+station[i]; //到下一加油i+1站希望的 行使的距离
		   if(s>n)
		   { //希望距离>n
 		        number++;//加油
		        s=station[i];//到下一加油站的距离
		        cout<<"在第"<<i<<"  个加油站加油"<<endl;
		   }
		}
	}
	cout<<number<<endl;
	return 0;
   }

运行结果：