遗传算法的简介与应用详细过程
写在前面
源程序参考原文:
遗传算法的简介与应用 - 子木的文章 - 知乎 https://zhuanlan.zhihu.com/p/49055485
写在前面
遗传算法是通过大量备选解的 变换、迭代和变异,在解空间中并行动态地进行全局 搜索的最优化方法.由于遗传算法具有比较完备的 数学模型和理论,在解决很多NP—Hard问题上具有 良好的性能.
1.因为我也是刚学遗传算法,我觉得它只是一个工具,会用就行,也没有去专门看书学习。然后就是只是在网上查查资料,网上很多教程都很详细,但是一些程序有些小错误。然后我写了几个程序,进行仿真。
2.网上的程序要么是单变量编码,或是二变量未编码。而我要做的是需要实现多函数多变量。所以这一篇只是介绍下遗传算法,以及它的基本实现方式,知道了它的实现原理就行了。
3.如果后面有时间的话,就把实现有偏好的多目标函数多变量寻求最优解的过程写写。
4.遗传算法实质就是在给定的自变量范围内找到函数的最大值,即最优解,如果是求最小值,理解成求最大值的倒数就行了。
5.欢迎指正
一、什么是遗传算法
遗传算法(Genetic Algorithm, GA)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
其主要特点是直接对结构对象进行操作,不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法,不需要确定的规则就能自动获取和指导优化的搜索空间,自适应地调整搜索方向。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;参数编码、初始群体的设定、适应度函数的设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。
遗传算法能够自我迭代,让它本身系统内的东西进行优胜劣汰的自然选择,把好的保留下来,次一点的东西就排除掉。遗传算法的本质就是是优胜劣汰,选出最优秀的个体,一般用来寻找最优解。
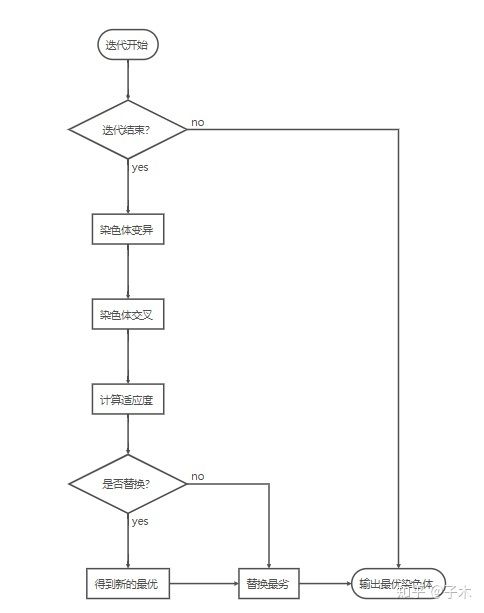
二、遗传算法框图和原理介绍
一次迭代包括以下几个过程:
- 染色体变异。即改变某个染色体的值;
- 染色体交叉。任意选择两个染色体交换部分基因;
- 计算适应度。计算每个染色体在当前迭代下对应的适应度。
- 优胜劣汰。选出下一代的染色体。
三、遗传算法的几个基本概念
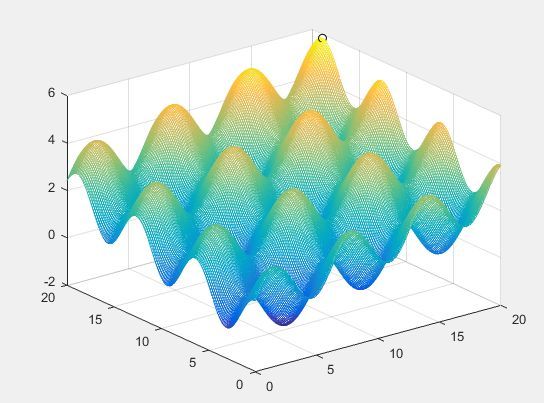
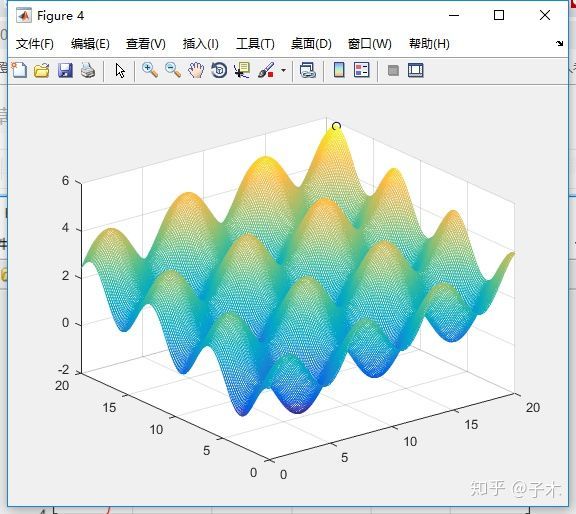
既然是应用,我直接举个例子,我觉得更容易理解,比如我现在需要求z=f(x,y)在x,y取值范围为(0,20)时的最大值。简单的函数可以手动求,但是假如是下图这样的呢?
Z =sin(X)+cos(Y)+0.1*X+0.1*Y
Z =sin(X)+cos(Y)+0.1*X+0.1*Y的三维图
为了第一次易懂,我直接把专业术语通俗点讲,当然,是我个人理解,如果有错,还望指出,一起学习。
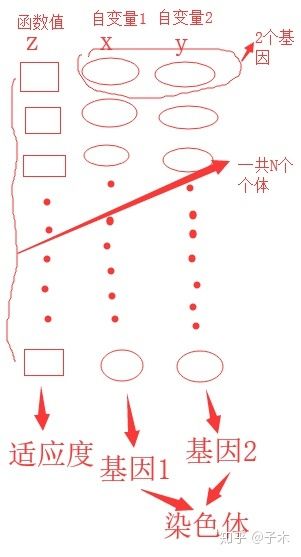
哈哈哈哈在旁边截了个图,然后随手编辑的,希望够形象,结合后面文字,应该可以很容易的理解了。
1)种群
首先,既然是遗传,寻找最优解,可以理解成找到最好的一个个体,那就得在一定的个体中去实现。这些所有的个体就构成了一个种群。在仿真中,自己规定种群的大小,比如z=f(x,y)的种群大小是N,也就是N个个体,它的意思就是在自变量的取值范围内随机取N个值,也就有N个函数值了。种群包含个体
2)个体
在一个种群中,有若干的个体,他们有着不同的特征。比如z1=f(x1,y1)就是一个个体,具体到自变量取了确定值后,这个个体也就所有信息都知道了。个体包含染色体和适应度
3) 染色体
一个个体对应一个染色体,染色体是个体基因的总称,比如z=f(x,y)中(x1,y1)就是其中的一个染色体。染色体包含基因
4) 基因
一个个体对应一个染色体,但是可以有多个基因。其实就是一个函数的多个自变量,比如z=f(x,y),则称该个体有2个基因。基因就是自变量
5) 适应度
一个个体在基因确定的情况下,它的适应度就确定了。比如z1=f(x1,y1),则z1的值就是该个体的适应度。适应度就是确定自变量后对应的函数值
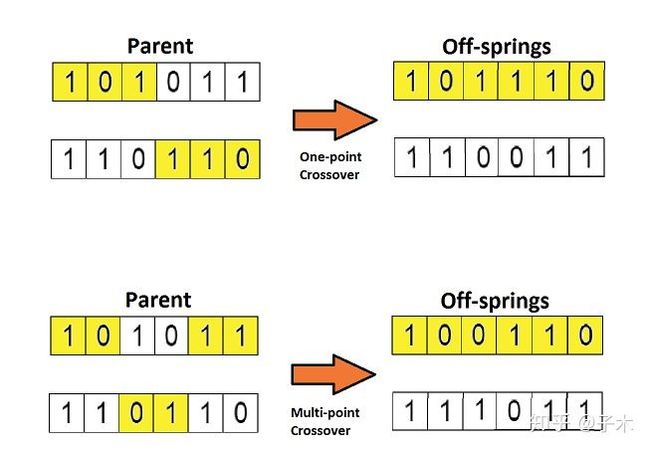
6) 交叉
染色体的交叉:N个染色体中,任意两个可能会交换染色体的某一部分基因。以一定概率通过互换两个父代个体的部分染色体产生新个体的运算。交叉运算是遗传算法核心算法之一,该算法在遗传过程中使用的频率最高,其目的是基于优良父代基因的基础上进一步扩展有限个体的覆盖面积。种群的发展影响着环境,环境也在选择适合生存的个体。
7)变异
染色体的变异:在发展的过程中,染色体自身可能发生某种突变,这里仅仅考虑某个基因的随机改变。将某一父代个体基因链的某些基因座上的基因值以某一概率作变动,形成新个体的运算。变异运算同样是遗传算法核心算法之一,旨在跳出局部搜索范畴,体现全区搜索的思想。
8)选择
优胜劣汰,自然选择。
建立在群体中个体的适应度评估基础上,将适应度值高的个体直接遗传到下一代或者通过交叉算子和变异算子产生新个体后再遗传到下一代。
我试过两种方法:
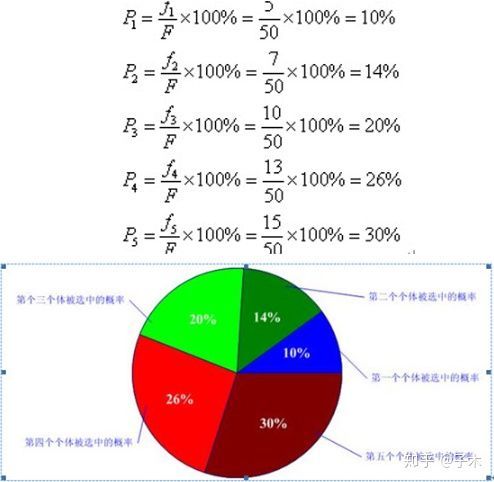
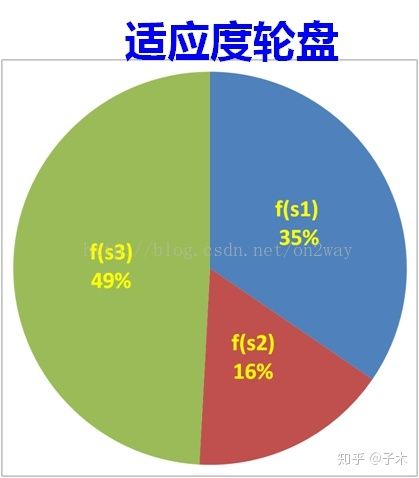
(1) 最常用的方法是轮盘赌法
原理是按照某个体的适应度在总适应度中的贡献来确定是否选择它,为技术的发展做出过贡献的老板,人们是不会忘记他的ヽ( ̄▽ ̄)ノ。
随便举个例子吧,假如算出的N个适应度分别是[1,3,5,9,7,6,8,2,8,7......8,7,3,8],
对其按升序排列,并依次求和,则所求的适应度之和也是升序排列。
假如总适应度是M(对所有适应度求和)并比喻作整个轮盘。
现在某种群发展协会召集所有个体来开一个会,干什么的呢?
选出对技术发展做出过突出贡献的人,并赋予它们交配权,
被我选中的人,你就可以拥有后代啦ヾ(゚∀゚ゞ)。
规则是什么呢?
按照你们N个个体的贡献度从小到大排好序,
你们每个人手里有一个数字,他是你及你以前所有个体的贡献度之和。
挨个上台抽签,盒子里装有N个数,分别是比适应度总和小的任意值,
个体上台之后从盒子里抽一个数,如果抽到的数比手里的数小的话,恭喜你,进入下一轮。
所以适应度大的染色体有更大的概率被选中,
这么说吧,假如某个个体的贡献度是8,适应度总和是10,那是不是只要抽到的数大于2的,这个个体就稳了呢。
那么如何实现轮盘赌法呢,具体参考程序。
(2)覆盖法
覆盖法就很粗暴了,直接用最优的覆盖掉交叉的,比如把适应度序列后面百分之20直接用最优的染色体覆盖。强者不但拥有交配权,还可以多生,多生,多生ヽ(°▽、°)ノ。
比较:我个人的理解是
选择轮盘赌法的原因是某个染色体这一代的适应度不好,但是有可能通过染色体变异和交叉后,下一代的适应度很好呢。所以采用概率的方式,不能一竿子把适应度差的全打倒。三十年河东,三十年河西,莫欺少年。。。。基因差?
5.另外一个概念就是编码
我使用的是二进制编码方式
实数编码:直接用实数表示基因,容易理解且不需要解码过程,但容易过早收敛,从而陷入局部最优
二进制编码:稳定性高,种群多样性大,但需要的存储空间大,需要解码且难以理解
- 编码、解码操作简单易行
- 交叉、变异等遗传操作便于实现
- 合最小字符集编码原则
- 利用模式定理对算法进行理论分析。
变异、交叉容易理解
二进制编码的缺点是:对于一些连续函数的优化问题,由于其随机性使得其局部搜索能力较差,如对于一些高精度的问题(如上题),当解迫近于最优解后,由于其变异后表现型变化很大,不连续,所以会远离最优解,达不到稳定
编码(coding):DNA中遗传信息在一个长链上按一定的模式排列。遗传编码可看作从表现型到基因型的映射。
解码(decoding):基因型到表现型的映射。
大概概念也就这些,具体的还是结合程序看。
遗传算法并不保证你能获得问题的最优解,但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解。而只要简单的“否定”一些表现不好的个体就行了。这就是遗传算法的精粹!
四、程序
最开始准备按照程序,一步一步的介绍,但是急着做其他的,就直接介绍附程序了。
程序的话是有多个函数,在一个文件夹里,不方便粘贴,有需要的直接留言,每天都在,看到了就发。
一共写了这几种,其实原理是一样的。
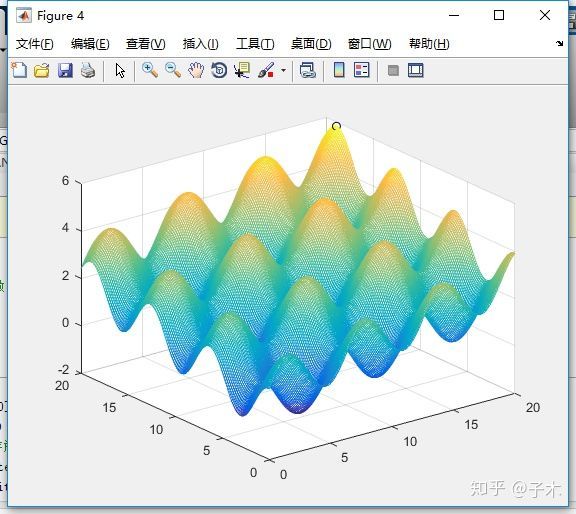
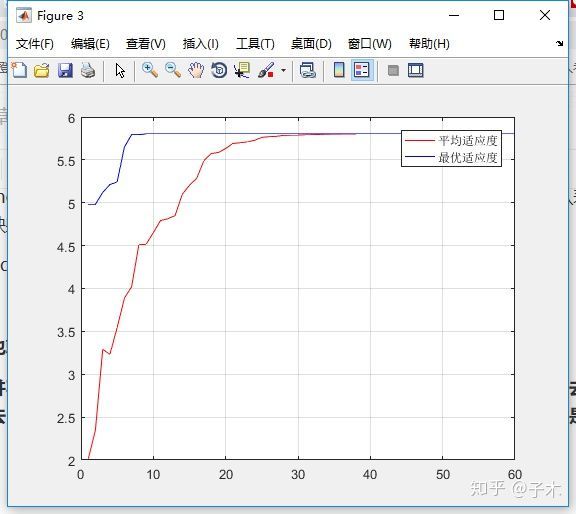
这是两个变量的仿真结果:
这是单变量的仿真结果:
最后,如果对你有所帮助,就点个赞呗。
( ㄕཀ ʖ̯ ཀ)