持续学习EWC代码实现
Overcoming catastrophic forgetting in neural networks
论文地址:EWC论文
论文代码:EWC代码,该代码包含大部分持续学习算法的代码
论文中公式推导论文:Elastic Weight Consolidation (EWC): Nuts and Bolts
关于论文的代码和公式推导CSDN上有几篇博客写的也挺不错,但是关于公式推导中的拉普拉斯变化,博客观点不统一,故本篇博客公式推导主要参考Elastic Weight Consolidation (EWC): Nuts and Bolts这篇论文。
一、持续学习简单介绍
持续学习指的是模型在完成新任务的同时不忘记旧任务如何完成的。由于神经网络存在灾难性遗忘,导致很难进行持续学习。目前,《A Continual Learning Survey: Defying Forgetting in Classification Tasks》这篇关于持续学习的综述将持续学习方法主要分为三类:
1.Replay Methods
2.Regularization-Based Methods
3.Parameter Isolation Methods
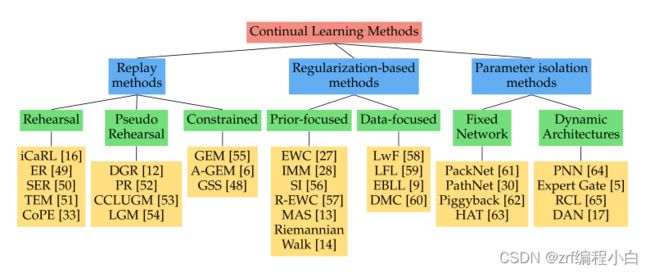
EWC属于第二类,基本思想是针对单个任务的神经网络中,有一些网络参数对完成该任务有着重要影响,为了保持对该任务的性能,应当让这些重要参数保持不变或者变化很小。
二、EWC主要思想
EWC主要从概率角度出发,推导出重要度矩阵用来度量网络参数对旧任务的重要程度并得到重要度矩阵即Fisher信息矩阵,为了让这些对旧任务重要的参数在完成新任务时变化不大,在训练新任务时添加了L2正则项并结合重要度矩阵来对完成旧任务重要的网络参数进行约束。
三、EWC公式推导
四、EWC代码实现
该代码为针对多任务的EWC实现,和两个任务的EWC实现不同点在于Fisher信息矩阵的处理,多任务的Fisher信息矩阵获得代码如下
# Fisher ops
if t>0: # t表示任务序号,从零开始
fisher_old={}
for n,_ in self.model.named_parameters():
fisher_old[n]=self.fisher[n].clone()
self.fisher=utils.fisher_matrix_diag(t,xtrain,ytrain,self.model,self.criterion)
if t>0:
# Watch out! We do not want to keep t models (or fisher diagonals) in memory, therefore we have to merge fisher diagonals
for n,_ in self.model.named_parameters():
self.fisher[n]=(self.fisher[n]+fisher_old[n]*t)/(t+1) # Checked: it is better than the other option,当t=0时,self.fisher=None
#self.fisher[n]=0.5*(self.fisher[n]+fisher_old[n])
Fisher的编程实现为(参考链接:2.如何计算Fisher信息矩阵)

关于Fisher信息矩阵的计算函数如下:
def fisher_matrix_diag(t,x,y,model,criterion,sbatch=20):
# Init
fisher={}
for n,p in model.named_parameters():
fisher[n]=0*p.data
# Compute
model.train()
for i in tqdm(range(0,x.size(0),sbatch),desc='Fisher diagonal',ncols=100,ascii=True):
b=torch.LongTensor(np.arange(i,np.min([i+sbatch,x.size(0)]))).cuda()
images=torch.autograd.Variable(x[b],volatile=False)
target=torch.autograd.Variable(y[b],volatile=False)
# Forward and backward
model.zero_grad()
outputs=model.forward(images)
loss=criterion(t,outputs[t],target)
loss.backward()
# Get gradients
for n,p in model.named_parameters():
if p.grad is not None:
fisher[n]+=sbatch*p.grad.data.pow(2)
# Mean
for n,_ in model.named_parameters():
fisher[n]=fisher[n]/x.size(0)
fisher[n]=torch.autograd.Variable(fisher[n],requires_grad=False)
return fisher
关于EWC的损失函数实现代码如下:
def criterion(self,t,output,targets):
# Regularization for all previous tasks
loss_reg=0
if t>0:
for (name,param),(_,param_old) in zip(self.model.named_parameters(),self.model_old.named_parameters()):
loss_reg+=torch.sum(self.fisher[name]*(param_old-param).pow(2))/2 # EWC的损失函数的正则化部分
return self.ce(output,targets)+self.lamb*loss_reg

