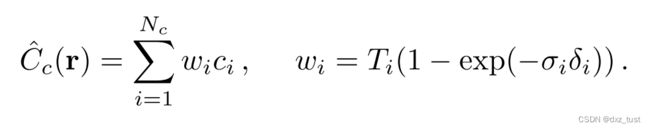NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

收录：eccv2020

领域：主要作用于神经场渲染以及视角合成

项目主页链接：NeRF: Neural Radiance Fields

主要贡献：

          1）引入了mlp预测像素颜色r以及volume density(体积密度，可以理解为不透明度，密度越大，越不透明）

          2）将position encoding （高频分量）引入训练网络，增强了其在高分辨率下的表征能力。

          3） 采用了层次采样的方式（为了更好的适应高分辨率的表征），先均匀采样（coase)，后随机采样（fine)

缺点：

        1）需要稠密的多视角图片，训练时间长

        2）对于非朗伯物质，合成的质量较差，并且存在伪影问题

整个pipeline：

输入：射线上采样点的位置x,y,z，以及射线方向

输出：采样点的颜色以及体积密度（rgb,volume density)，最后通过离散渲染方程得到与该条射线相交的平面像素值的颜色。

       首先来熟悉一下这篇文章中最重要的公式，渲染方程（也叫反射方程，t 的近段和远端边界分别为 tn 以及 tf 。那么这条射线的颜色，则可以用积分的方式表示为（t可以理解为射线从起始点到终止点的路径）：

其中 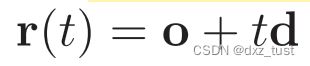，o表示射线原点，t表示位置或者是边界，d表示射线的方向,上述是用，这两个变量表示的；σ(t)表示光线到到路径t的终止概率；T(t) 是射线从 tn 到 t 这一段路径上的累积透明度，可以被理解为这条射线从 tn 到 t 一路上没有击中任何粒子的概率。

        1）从上面公式C(r)中可以看出采样点的体积密度σ只和采样点的位置r(t)有关，但是采样点的颜色c既和位置r(t)有关，也和该处射线的方向d有关；这也验证了一个基本结论：不同方向看同一个点，颜色是不一样的；

        2）T(t) 有点类似于加权的思想；假若某个采样点的前面有很多物质，那么该点的密度就会变高，随之T(t)就会变小，T(t)小，那么该采样点对整体颜色贡献就小。因为我们只关心想关心射线刚开始遇到粒子/物质的点，并不想关心它之后的点，所以这里要设置一个T(t)来降低后面采样点对整体颜色的贡献值；

       3）整个C(r)就可以表示为：最终成像平面上某点的颜色值=该条射线上所有点（采样点）所辐射的颜色达到该平面的累积值；

由于计算机无法计算连续积分，所以该篇文章中将上面连续的C(r),转变成近似离散的形式，如下：

       N表示采样点的数量；δi = ti+1 − ti表示为两个连续采样点之间的距离 ，其他的和上述公式中的含义一样；

关于引入高频分量：

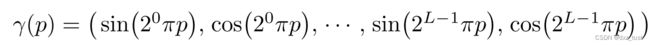
         其中文中对于位置(x,y,z),L设置为10，对于方向，L设置为4；注意这里是每个变量分别输入，比如这种形式

关于采样点的采样策略（分层采样）：

     首先用均匀采样方式采样射线上64个点，然后由这64点的密度值估计出（PDF)密度分布函数。再使用逆采样算法集中对高密度的区域采样128点。使用该策略可以提高采样的效率，不需要对射线上所有区域都进行密集的采样,这样大大提高了效率，节省了很多训练时间。

        针对上述两次采样，文中分别把这两个采样阶段当作coarse network和fine network，下面是“coarse sample”公式，N为采样数，tn为采样起始点，tf为采样终止点

并且文中先利用 coarse sample通过 coarse network 粗略的计算一下颜色，公式如下：

注意这里的​​   ​​​和上面的还不一样，上面的是在fine network 阶段使用。

 fine sample中每个 PDF 定义：，Nc为 coarse sample的数目；

通过这个对每个高密度区域逆采样128个点+之前coarse sample 64个点作为 "fine network" 的输入。

损失函数构成： 

 由两个部分构成：一个是coarse network 输出的rgb和gt 做L2，另外一个则是fine network 输出的rgb和gt 做L2

单个场景重建的耗时：

 评测数据集以及指标：

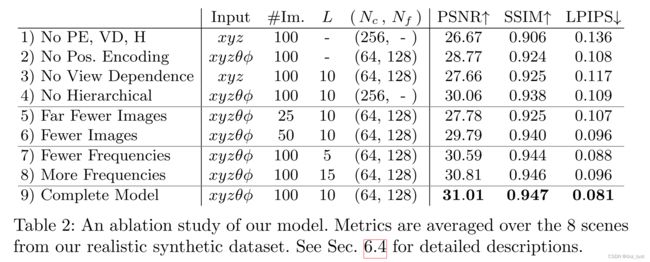
 消融实验

 主要对比了position encode、view dependence、hierarchical sample三个条件。

 未来工作可探索的方向：

        1）更高效的优化方式、以及渲染方式

        2）本文所用的基础采样来自于2d像素点，能否尝试下基于voxel grid以及mesh的采样