Python求解方程组与Pytorch实现梯度下降
练习一
解下列方程组:
{ x + 2 y + z − 2 w = 0 2 x + 3 y − w = 0 x − y − 5 z + 7 w = 0 \left\{\begin{array}{l} x+2 y+z-2 w=0 \\ 2 x+3 y-w=0 \\ x-y-5 z+7 w=0 \end{array}\right. ⎩ ⎨ ⎧x+2y+z−2w=02x+3y−w=0x−y−5z+7w=0
验证R(A)与R(A, B)与未知数数量
分别计算R(A)与R(A, B)
import numpy as np
A = np.array([[1, 2, 1, -2], [2, 3, 0, -1], [1, -1, -5, 7]])
B = np.array([0, 0, 0])
B = B.reshape(B.shape[0], 1) # 把B转置为列向量
print("系数矩阵的秩R(A):", np.linalg.matrix_rank(A))
AB = np.hstack((A, B)) # 按顺序水平排列数组
print("增广矩阵的秩R(A, B):", np.linalg.matrix_rank(AB))
系数矩阵的秩R(A): 2
增广矩阵的秩R(A, B): 2
由上述代码可知,R(A) = R(A, B) = 2,但未知数的个数为4,只能利用Sympy库solve()函数求解
Sympy库solve()函数求解
from sympy import *
x, y, z, w = symbols("x y z w")
Eq = [x + 2*y + z - 2*w, 2*x + 3*y - w, x - y - 5*z + 7*w]
res = solve(Eq, [x, y, z, w])
print("结果:", res)
结果: {x: -4*w + 3*z, y: 3*w - 2*z}
练习二
解下列方程组:
{ x + 2 y + z = 2 x + 2 y + 4 z = 3 x + 3 y + 9 z = 5 \left\{\begin{array}{c} x+2 y+z=2 \\ x+2 y+4 z=3 \\ x+3 y+9 z=5 \end{array}\right. ⎩ ⎨ ⎧x+2y+z=2x+2y+4z=3x+3y+9z=5
验证R(A)与R(A, B)与未知数数量
分别计算R(A)与R(A, B)
import numpy as np
A = np.array([[1, 2, 1], [1, 2, 4], [1, 3, 9]])
B = np.array([2, 3, 5])
B = B.reshape(B.shape[0], 1) # 把B转置为列向量
print("系数矩阵的秩R(A):", np.linalg.matrix_rank(A))
AB = np.hstack((A, B)) # 按顺序水平排列数组
print("增广矩阵的秩R(A, B):", np.linalg.matrix_rank(AB))
系数矩阵的秩R(A): 3
增广矩阵的秩R(A, B): 3
由上述代码可知,R(A) = R(A, B) = 3 = n,即系数矩阵的秩等于增广矩阵的秩等于未知数的个数为3,可以通过三种方法求解求解
利用逆矩阵求解
A_inv = np.linalg.inv(A)
X = A_inv.dot(B)
print("通过逆矩阵求得X:\n", X)
C = np.dot(A, X)
print("比较求出的X是否为解:", np.allclose(C, B))
通过逆矩阵求得X:
[[1. ]
[0.33333333]
[0.33333333]]
比较求出的X是否为解: True
通过np.linalg.solve()求解
X_lg = np.linalg.solve(A, B)
print("通过np.linalg.solve()求解得X:\n", X_lg)
print("比较求出的X是否为解:", np.allclose(np.dot(A, X_lg), B))
通过np.linalg.solve()求解得X:
[[1. ]
[0.33333333]
[0.33333333]]
比较求出的X是否为解: True
Sympy库solve()函数求解
x, y, z = symbols("x y z ")
Eq = [x + 2*y + z - 2, x + 2*y + 4*z - 3, x + 3*y + 9*z - 5]
res = solve(Eq, [x, y, z])
print("结果:", res)
结果: {x: 1, y: 1/3, z: 1/3}
练习三(梯度下降法)
min f ( x , y ) = x − y + 2 x 2 + 2 x y + y 2 \min f(x, y)=x-y+2 x^{2}+2 x y+y^{2} minf(x,y)=x−y+2x2+2xy+y2
初值 ( x 0 , y 0 ) = ( 0 , 0 ) T \left(x_{0}, y_{0}\right)=(0,0)^{T} (x0,y0)=(0,0)T,步长0.0008, f ( x n ) − f ( X n − 1 ) f(x_n)-f(X_{n-1}) f(xn)−f(Xn−1)的绝对值小于7e - 9时可以终止
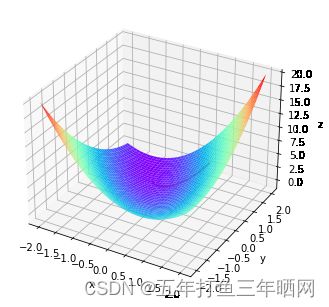
此处尝试通过pytorch完成自动求导与梯度下降,并使用Matplotlib画出函数图形
import numpy as np
import torch
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def func(x, y):
return x - y + 2*x**2 + 2*x*y +y**2
def gradient_descent(x, y, lr, iters):
# 把x、y设置为可求导变量
x = x.clone().detach().requires_grad_(True)
y = y.clone().detach().requires_grad_(True)
tag_x, tag_y, tag_z = [], [], []
tag_x.append(x.item())
tag_y.append(y.item())
tag_z.append(func(x, y).item())
for i in range(iters):
f = func(x, y)
f.backward() # 自动反向求导,获得x.grad和y.grad
last_f = f
x.data -= lr * x.grad
y.data -= lr * y.grad
# 每一次更新grad后数值会保存在x和y中,所以要及时将x.grad和y.grad清零
x.grad.zero_()
y.grad.zero_()
tag_x.append(x.item())
tag_y.append(y.item())
tag_z.append(func(x, y).item())
if abs(last_f.item() - func(x.data, y.data).item()) < 7e-9:
break
return x, y, func(x, y), tag_x, tag_y, tag_z
def visulization(tag_x, tag_y, tag_z):
fig = plt.figure()
ax = Axes3D(fig, auto_add_to_figure=False)
fig.add_axes(ax)
X, Y = np.mgrid[-2:2:40j, -2:2:40j]
Z = func(X, Y)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap="rainbow")
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.plot(tag_x, tag_y, tag_z, 'r')
plt.show()
x = torch.ones(1)
y = torch.ones(1)
lr = 0.0008 # 学习率(步长)
max_iter = 1000 # 最大迭代次数
x, y, f, tag_x, tag_y, tag_z = gradient_descent(x, y, lr, max_iter)
visulization(tag_x, tag_y, tag_z)
print("最低点x坐标:", x.item())
print("最低点y坐标:", y.item())
print("最低点:", f.item())
最低点x坐标: -0.5603159666061401
最低点y坐标: 0.8297014832496643
最低点: -1.0034949779510498