PyTorch框架torch.nn实现Logistic回归

本文主要总结实现torch.nn实现Logistic回归的方法。Logistic回归[只借助Tensor和Numpy相关的库]在人工构造的数据集上进行训练和测试。

PyTorch

2016年10月发布PyTorch，是专注于直接处理数组表达式的低级别API。其前身是Torch，被Facebook人工智能研究所大力支持。PyTorch现在是学术研究的首选解决方案。该框架的主要缺陷是，导出的模型难以移植，工业中的应用和部署不成熟，代码冗余量较大。优点为简单易用，社区活跃以及代码简洁。在运行方式上，PyTorch是基于张量和有向非循环图[DAG]，有向非循环图是内置的，可以随时定义、随时更改、随时执行节点，相当灵活。在训练模型上，PyTorch在分布式训练比较欠缺，需利用异步执行的本地支持来实现。

机器学习基础

机器学习，英文为Machine Learning，简称ML。在周志华老师“西瓜书”中，机器学习所研究的主要内容是关于在计算机上从数据中产生“模型”的算法。在[神经网络与深度学习]一书中，机器学习通常指一类问题以及解决这类问题的方法，即如何从观测数据[样本] 中寻找规律，并利用学习到的规律[模型]对未知或无法观测的数据进行预测。

机器学习的三大基本要素为：模型、学习准则、优化算法。

• 模型：指输入空间到输出空间的函数映射
• 学习准则：用于评价模型好坏
• 优化算法：可理解为在假设空间中找到最优模型的方法

输出的标签是连续值，一般称之为回归问题。输出目标是一些离散的标签，则被称之为分类问题。Logistic回归，虽然叫回归，但其实是分类模型，是将分类决策问题看作条件概率估计问题是，解决二分类问题的。

模型：

1. 用线性函数组合特征； 
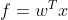2. 引入非线性函数g[]来计算类别标签的条件概率，把线性函数的值域从实数区间“挤压”到了[0,1]之间，可以用来表示概率。这个非线性判别函数的作用是，预测给定输入x属于不同类别的一个后验概率。x的取值范围是负无穷到正实数域的值；
3. 该非线性函数选择Logistic函数，Logistic函数：​​​​​​​​​​​​​​。

学习准则：即如何定义损失函数的问题，模型预测的条件概率和真实条件概率的之间的差异。引入了熵的概念，熵用来衡量一个随机事件不确定性，熵越大随机变量信息越多。

优化算法：梯度下降方法

实现过程

Torch.nn模块是Pytorch为神经网络设计的模块化接口，定义了不同的网络层。Torch.nn 利用autograd来定义模型，数据结构为Module。代码运行在Python 3.9.7版本以及Pytorch 1.10版本中。代码均在pycharm上运行，均能完美运行。

导入本次实验所需的包或模块

import torch                                            #导入pytorch框架
import numpy as np                                      #导入numpy包
import random                                           #导入random包

生成数据集

随机生成实验所需要的二分类数据集，0、1数据

# 随机生成实验所需要的二份类数据集x1和x2，分别对应的标签y1和y2.
n_data = torch.ones(50, 2)                              #数据的基本形态
x1 = torch.normal(2 * n_data, 1)                        # 正态分布 shape=(50, 2)
y1 = torch.zeros(50)                                    # 类型0   shape=(50, 1)
x2 = torch.normal(-2 * n_data, 1)                       # 正态分布 shape=(50, 2)
y2 = torch.ones(50)                                     # 类型1   shape=(50, 1)
# 由于有50组数据，进行8：2划分，训练集为40组，测试集为10组
num_inputs = 2
train_examples = 40
test_examples = 10
train_input=torch.cat((x1[:train_examples], x2[:train_examples]),0).type(torch.FloatTensor)
train_output=torch.cat((y1[:train_examples], y1[:train_examples]),0).type(torch.FloatTensor)

读取数据

Data库来读取数据，在每一次迭代中，使用Data随机读取。

def data_iter(batch_size,features,labels):
    num_examples=len(features)
    indices=list(range(num_examples))
    random.shuffle(indices) # 样本的读取顺序是随机的
    for i in range(0,num_examples,batch_size):
        j= torch.LongTensor(indices[i:min(i+batch_size,num_examples)]) # 最后一次可能不足一个batch
        yield features.index_select(0,j),labels.index_select(0,j)

构建模型

继承nn.Module，然后构建网络。

class LogisticNet(torch.nn.Module):
    def __init__(self,n_features):
        super(LogisticNet,self).__init__()
        self.linear=torch.nn.Linear(n_features,1)
        self.sigmoid=torch.nn.Sigmoid()
    # forward 定义前向传播
    def forward(self, x):
        x = self.linear(x)
        x = self.sigmoid(x)
        return x

损失函数和优化

使用交叉熵函数作为本实验的损失函数。在实验中，我们首先需要把真实值变成与预测值相同的形状。并利用sgd函数实现小批量的随机梯度下降算法，通过不断迭代模型参数来实现损失函数的优化。

# 损失函数
loss=nn.BCELoss()
# 优化算法
optimizer=torch.optim.SGD(logistic_model.parameters(), lr=0.03)

模型训练、测试

在整个训练过程中，模型会多次迭代并更新参数，读取小批量数据样本特征和标签，并利用backward计算随机梯度，调用sgd函数优化模型参数。