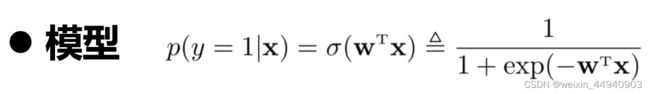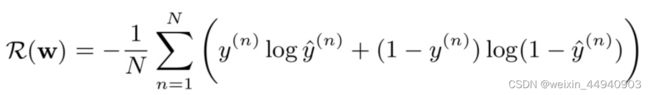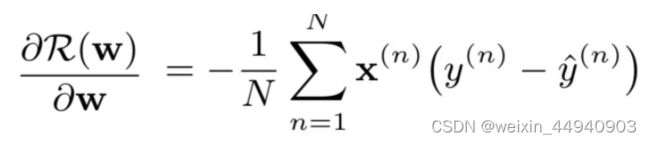PyTorch框架从零实现Logistic回归（非torch.nn）

本文主要动手从0实现Logistic回归（只借助Tensor和Numpy相关的库）在人工构造的数据集上进行训练和测试。

机器学习基础

机器学习，英文为Machine Learning，简称ML。在周志华老师“西瓜书”中，机器学习所研究的主要内容是关于在计算机上从数据中产生“模型”的算法。在《神经网络与深度学习》一书中，机器学习通常指一类问题以及解决这类问题的方法，即如何从观测数据(样本) 中寻找规律，并利用学习到的规律（模型）对未知或无法观测的数据进行预测。

机器学习的三大基本要素为：模型、学习准则、优化算法。

• 模型：指输入空间到输出空间的函数映射
• 学习准则：用于评价模型好坏
• 优化算法：可理解为在假设空间中找到最优模型的方法

输出的标签是连续值，一般称之为回归问题。输出目标是一些离散的标签，则被称之为分类问题。Logistic回归，则是将分类决策问题看作条件概率估计问题。

1. 用线性函数组合特征
2. 引入非线性函数来计算类别标签的条件概率，把线性函数的值域从实数区间“挤压”到了(0,1)之间，可以用来表示概率
3. 该非线性函数选择Logistic函数

 

 

 利用PyTorch框架从零实现Logistic回归

代码运行在Python 3.9.7版本以及Pytorch 1.10版本中。

1、生成数据集

随机生成实验所需要的二分类数据集。通过在Pycharm中键入如下代码，构造一个简单的数据集。

# 导入所需要的报或模块
import torch                                            #导入pytorch框架
import matplotlib.pyplot as plt                         #导入matplotlib包
# 随机生成实验所需要的二份类数据集x1和x2，分别对应的标签y1和y2.
n_data = torch.ones(50, 2)                              #数据的基本形态
x1 = torch.normal(2 * n_data, 1)                        # 正态分布 shape=(50, 2)
y1 = torch.zeros(50)                                    # 类型0   shape=(50, 1)
x2 = torch.normal(-2 * n_data, 1)                       # 正态分布 shape=(50, 2)
y2 = torch.ones(50)                                     # 类型1   shape=(50, 1)
# 注意 x, y 数据的数据形式一定要像下面一样 (torch.cat 是合并数据)
x = torch.cat((x1, x2), 0).type(torch.FloatTensor)
y = torch.cat((y1, y2), 0).type(torch.FloatTensor)
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
plt.show()

2、读取数据集 

## 读取数据
def data_iter(batch_size,features,labels):
    num_examples=len(features)
    indices=list(range(num_examples))
    random.shuffle(indices) # 样本的读取顺序是随机的
    for i in range(0,num_examples,batch_size):
        j= torch.LongTensor(indices[i:min(i+batch_size,num_examples)]) # 最后一次可能不足一个batch
        yield features.index_select(0,j),labels.index_select(0,j)

3、构建模型

在构建模型之前，首先将权重初始化成均值为0、标准差为0.01的正态随机数，偏置初始化为0。其次，设置requires_grad=True，以需要这些参数来求梯度迭代参数的值。最后，利用mm函数和pow函数作矩阵运算，实现Logistic回归的模型。

## 构建模型
# 将权重和偏置初始化
w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)
# 设置梯度，来迭代参数的值
w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)
# 利用torch.mm和torch.pow函数实现logistic回归的模型
def logistic(X,w,b):
    y = 1/(1+torch.pow(np.e,-torch.mm(X,w)+b))
    return y

4、定义损失函数和优化算法

使用手编的二元交叉熵函数作为本实验的损失函数。在实验中，我们首先需要把真实值变成与预测值相同的形状。并利用sgd函数实现小批量的随机梯度下降算法，通过不断迭代模型参数来实现损失函数的优化。

5、训练和测试模型

在整个训练过程中，模型会多次迭代并更新参数，读取小批量数据样本特征和标签，并利用backward计算随机梯度，调用sgd函数优化模型参数。

具体代码见：https://mianbaoduo.com/o/bread/Yp2ak59q