利用numpy实现Logistic回归模型——总结（1）

学习总结

买了一本书《飞桨PaddlePaddle深度学习实战》，这本书第三章的一个实例，花了大概一整天的时间慢慢地研究了一下这个Logistic回归模型，把书中的这个例子算是看明白了。把这一整天的理解总结出来，免得时间一长，把这一整天的内容给忘了，方便自己日后快速了解回忆。

第一：深度学习单层网络

总结：Logistic回归模型是简单的单层网络
怎么理解单层网络，我的理解是，就是按照一个流程走完就可以出结果，每一个步骤在外在的表现上只走了一遍（可能他内部走了很多个循环，但是他被打成一个包包，这个过程他就走了一遍）。

第二：Logistic回归模型概述

2.1建立一个数学模型：把变量和结果表示出来——线性变换出来吧

书中给出的例子是医学上的判断是否感染肺癌 y={0，1}，0，1的物理意义是：0：没有患肺癌，1：患有肺癌。
那么现实生活中影响一个人患病的因素可以有很多种，这里是变量，x1,x2,x3,x4,x5,…xn,每一个因素前面都有一个系数，就是权重，比如年龄，是否吸烟呢，吸烟和年龄相比，可能吸烟所占的比重就大一点，那么吸烟的权重就大。那么用方程表示就是
y=w1x1+w2x2+w3x3+…+wnxn+b ——式子1
这样就用数学公式表示出来了这个医学模型（是很简单，但是没用呀）。
这样表示出来是没有用的，如果这样可以表达的话，什么我都能表达出来。。。。。。
通过线性代数的知识我们可以知道上面的式子1是矩阵相乘的展开式
那么是那两个矩阵相乘的展开式呢（我还不会用这个写博客，我先用纸写吧，拍个照片上来）


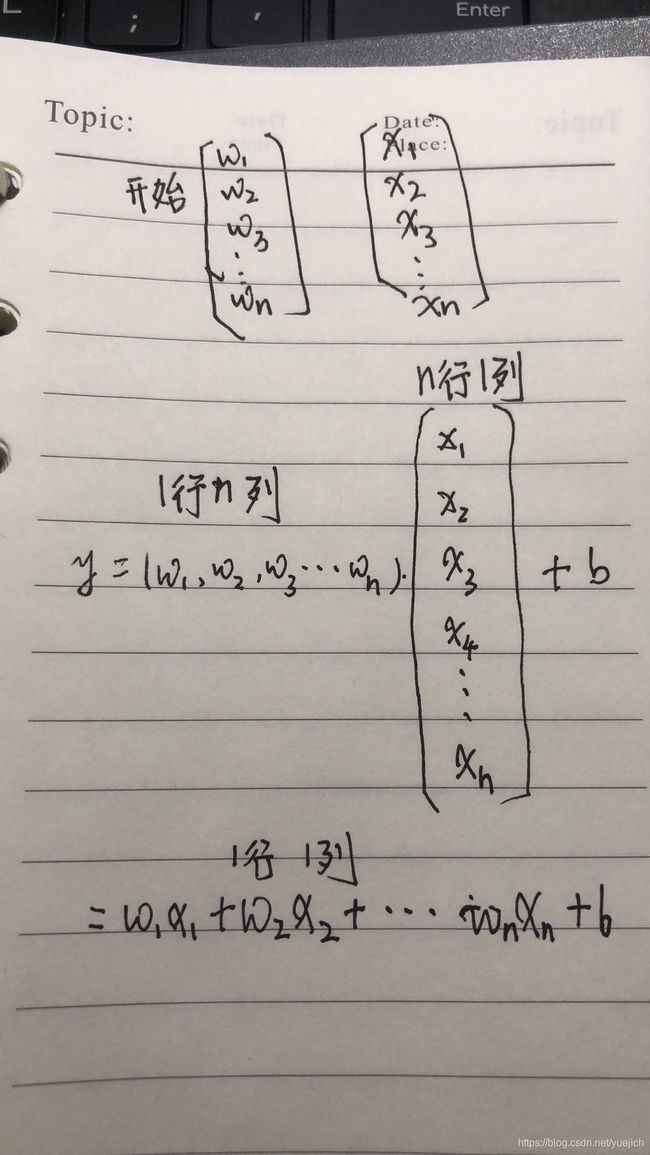
也把线性代数里面的这一页也拍了一个照片贴了上来（其实很简单，关于矩阵的加减乘除运算可以看看线性代数这个课本）
那么这个n元一次方程就可以用矩阵（也可以用向量）表示：
y=W.T*X+b (这里用大写字母表示矩阵和向量)
关于为什么.T，是因为矩阵的运算得出的，因为W和X是一样的，都是n行1列，既然W乘以X，需要将W转置一下，变换成1行n列，这样算出的是一个数。

2.2 怎么把y值映射到0和1这两个数——非线性变换出来了

上一个2.1中，y我们用x表示出来了，我们知道影响因素x有年龄，年龄可以从1到100的范围选值，可以1岁，可以是10岁，可以是80岁，这些年龄患病的概率是不一样的，如果权重是5吧，1岁患病是5，10岁患病是50，
我们再加入一个因素是吸烟的烟龄，也可以是1年，2年，3年，比如权重是8，得出1年是8，2年是16，3年是24，
等等
那么这些数加起来后得到是一个y值，比如y=50，10，1000，1259等，这些数值怎么映射到0和1来表示患病和不患病呢
这样很难了，难道用个if else判断，大于多少是患病，小于多少是不患病吗？感觉这样也可以，但是是不是很简单了，结果会不会不准确。
这就引出了非线性变换的函数
sigmoid（）

数学就是这么好，有这么一个函数，他的图像是上图这样的，别管x值是多少，他的y值要么落在1上，要么落在0上，所以无论你的数据有多少，这个函数都能把这个数映射到1或者0上。
但是物理意义是什么，怎么理解，我也不知道，但是这个算法算出来的结果就是对，你说气人不气人，所以别管其他的，这样得出的结果是对的就完了，也不用深究，就知道这么用就行了。毕竟用我们能理解的if else算出来的结果不怎么样。（这些都是我猜的）
这个函数的表达式是z=1/1+e^(-y)
通过上一步算出y值，把y值代入到这个函数，得到z，看看z是1还是0
如果z=1那么就是患病，如果z值等于0就是不患病
总结：这一个流程到此结束，这就是我对Logistic回归模型的理解

第三：Logistic回归模型——预测步骤之理解

通过上面我们知道了：
第一步：要算出y值，y值是一个连续的值，
第二部：要把这个y值通过非线性变换转换成0和1
那么先算出y值
y=w1x1+w2x2+w3x3+…+wnxn+b
这里的X我们知道，是样本数据，y也知道，是样本标签，只有b和W不知道
所以第0步就是算出W和b
那么问题来了，怎么算出W和b？
接下来的流程就好理解了，不理解就不理解在哪些数学公式上，毕竟都这些数学公式都是这么的抽象，很难有具体的物理现象和这些公式映射，不过不要紧，先理解了过程再说。
计算机就是有这样的一个好处，比如说x+y=5，让你算x=？，y=？，假装很难算，但是计算机就可以算出来，先让x=0，y=0，然后x不变，让y一点一点的往上加，注意这里的一点一点的就是这个logistic回归模型里面讲的梯度，开着电脑，让他一点一点的实验，我们先去睡觉，看看他什么时候能算出来x和y。

回到这个问题中的W和b，也没有那么高级，也是先给他一个初始值，让他按照梯度，一点一点的往上加不断的改变W的值，没改变一次W的值，通过计算算出一个y值，让真实的y值和这个预测出来的y值相减求”差“，这个”差值“越小，则算出的（不如说是实验出的）W和b距离正确值越近，其实没必要百分百和真实的W和b一样，也不可能百分百和他们一样，再说了W和b到底是多少也没人知道。
整理一下这个过程：
第一：给出W和b的初始值，带入到这个线性方程求出z，通过非线性变换映射到0和1
第二：把每一条数据集里面的数据全部带入到这个方程，通过这个方程算出预测的y值
第三：把数据集里面的真实的y值和预测的y值求差，看看他们差多远来决定是不是继续猜
总结：
现在通过初始化W和b值，得出了y的预测值，也就是说我们瞎猜了一个W和b，通过瞎猜的系数求出了y值，这个准确率很低，毕竟是瞎猜的吧，所以这个预测值也是瞎猜的，现在看看你这个瞎猜的值和真实值的距离，举个例子，老王家有三个儿子一个姑娘，让你猜老王家有几个孩子，我第一次猜了：老王家有两个孩子，真实有四个，4-2=2，回答：不对，你这差的多，比这个多，多好几个呢，你下次猜加上一个，有三个，不对，比这个多，有四个，这样就会越来约接近正确的值。这时候就需要定义一个损失函数和成本函数

第四Logistic回归模型——损失函数和成本函数

上一步算出了y的预测值，加上我们本来就知道的真实值（样本里面有），我们都知道了，现在就到了判断了，判断预测的值对不对，直观的理解，我们是用真实值减去预测值的绝对值的大小来判断这个预测的靠谱不靠谱，比较常用的也有均方差损失函数，平方损失函数，但是这个Logistic回归模型用的是对数损失函数又叫做对数似然损失函数
什么是平方损失函数呢？
这本书上给出了公式
L(y预测，y）=（y预测-y）^2/2
就是预测值和真实值差的平方除以2
这样也不难理解 数值越大，预测越离谱
那什么又是对数损失函数呢？
这本书上面也给出了公式
L(y预测，y）=-[y*logy预测+(1-y)log(1-y预测）]

至于为什么不直接用差，或者用别的我也不知道，虽然书中给出了证明，勉强也能说服自己，但是还是不能说理解了。可能是实验证明吗，就像上面说的映射到0和1的sigmoid（）函数一样，物理意义比较抽象，理解不了，不好理解。
这个损失函数里面就是预测值是未知量，每一个W和b的值都会计算出一个预测值，只是这个预测值是按照一定的规律在变化的，通过训练结果表明，这个规律是啥我不知道，但是这个规律使得这个损失值不断的减小。
上面说的是一条样本，算出一个损失值，那么这个训练集有n条样本，这个n的数量级可以很大，那么这本书就引入了成本函数的概念。
n条样本就算出了n个预测值，每个预测值相对于真实值计算，得到了一个损失值 L(y预测，y)
总共有n个L值，那么问题来了
怎么通过这些数据科学的计算出这个损失和成本是真实的呢？
其实这个问题不好理解，
书中用的是所有损失求和算平均值的方法得出的一个成本函数J,
J=(L1+L2+L3+…+LN)/n
这个J 就是成本函数，至于这样科不科学我也不知道，你就知道：他们是这么做的，训练结果也可以就行了。
总结：
到这里了，开始总结一下，
给我们数据以后，我们知道数据集里面的 x和y的真实值
瞎猜给定初始值后，我们知道线性方程里面的w和b
这样我们可以把y预测用w ，b， x表示出来，
因为是二分类用到了非线性变换sigmoid（）函数
这样给y预测做了一个变形，y预测表示维 sigmoid（w,b,x)
继续
算损失和成本
L=y-y预测（我这里省点事，这里的减号理解成物理含义上的减号就行）
L是关于y和y预测的函数
y预测可以用w，b，x表示
则L也可以用这些表示
引入到整个数据集
成本函数J就是n个L的叠加后求平均
则J也是可以用w，b，x表示
可以把J写成一个方程式
J=f(W,b)
因为x和y都是已知量
W,b是我们要一点一点实验得出的（这个一点一点是不是熟悉，上面提到过，就是梯度），现在我们就是要计算在(W,b）等于多少的时候J的值最小的问题，这个J的方程现在是确定的了，有线性方程+sigmoid（）方程+对数损失方程
到这里是不是就理解了整个计算的物理意义了。（哈哈）
下面就引入了梯度概念，梯度下降算法，来解这个Logistic模型。

第五：Logistic回归模型——梯度下降算法

J=f(W,b)
现在问题简化了，现在的问题是在W,b取什么值的时候，J取最小值的问题。
我们知道f(x)=x^2,这个函数在x=0的时候f(x)取最小值，他的图像是一个抛物线，我们先知道他的图像是一个抛物线，对他求导导数是2*x，导数的物理含义就是抛物线上斜率，斜率为0，我们可以算出x=0是斜率为0.因为我门知道他的图像是一个抛物线，而且是开口向上，所以在他斜率为0的点的值最小，

这个J(W,b）怎么弄呢？也是通过抛物线这个延伸，对这个求导，应为W是一个n为向量，这个就是求偏导，具体的物理含义我也忘了，这个应该是高等数学里面的知识，里面应该有物理例子给出。
总结
总之：从上一节的损失函数和成本函数我们可以知道J是一个数，当W,b确定的情况下的一个成本值，
由于这个函数是确定的了
那么dw和db可以通过数学方法计算出：

里面的z就是没有sigmoid（）之前的y的预测值，可以用x，y表示

第六：Logistic回归模型——向量化

再说

第七：Logistic回归模型——利用Numpy实现Logistic回归模型

再说

总结：个人理解

个人理解：通过对这个深度学习模型的学习（自己重新手写并在电脑上写了共两遍代码），让我又复习了一下数学知识（还好高中/大学的数学知识没有全部忘记），主要的数学知识有“偏导数”，“向量”，“矩阵”，“矩阵的加减乘除运算法则”，等等，好像就这些吧！这些数学概念的物理含义不好理解，好在上学的时候总结过，凭记忆偏导数的物理含义不好说，好像是含有多个变量的函数在对某一个变量求导，其他变量不求导，比如蔬菜的价格受到天气和温度两个因素的影响，抛开天气不说，单纯的温度这个变量对蔬菜价格影响多少，这个理解一下也知道是片面的，因为是两个因素影响的，你抛开一个不说，只说一个肯定不行，这样的导数是偏导数，这个概念是很有物理意义的，对于线性函数来说，这个导数就求出了一个标量数值，这个数值就是影响蔬菜价格在这里所占的“权重”，列个方程式就是y表示蔬菜价格，是一个“因变量”，变量是温度t和天气w吧，因变量y肯定和变量t和变量w有关系，什么关系我们不知道，假设他们是线性关系，可以列出方程式y=at+bw+c，c这里是偏置，是一个标量，这个方程式就是一个多个变量的一次方程，也就是线性函数。高等数学中求偏导的方法是这样的：现在对变量t求偏导数，则b*w+c就是一个实数，求导等于0，这dy/dt=a，这个a就是偏导数，同理对变量w求偏导数，可以得到dy/dw=b，以此类推，如果是一个更多变量影响“因变量“的一个线性方程（注意：这里都是说的线性方程）对每一个变量求偏导就会得到一个标量的数值，这个数值就是这个变量前边的系数，这样就很容易理解”权重“这个词的物理含义了吧（哈哈）！！！
继续说我的理解：每个变量前面的这个系数越大对结果的影响越大，系数越小对结果的影响越小，再说这个偏置也好理解他的物理含义，毕竟没有各个变量的时候蔬菜也有价格，如果价格是0，那么这个偏置就是0，如果这个价格开始就是一个数，那这个偏置就是这个数，这就是对一元一次方程的延伸。
对于一个样本来说，他有n个变量，结果就有一个0或者1，n个变量决定这个结果，那么他的偏导数就是一个n行1列的一个矩阵，或者说是行列式，其实说矩阵更好，因为在大学的线性代数里面说的好像式矩阵的运算，矩阵有什么加减乘除等方法可以运算并且得到结果。
再说说矩阵和向量，我理解的就是向量就是一个”一维“的矩阵（时间长了，不知道这里用一维这个概念对不对，总之方便理解），那么矩阵就是多维的向量。
向量的物理意义好理解，物理中的力就可以看成一个向量，他是有方向有大小的一个东西。