利用numpy实现Logistic回归模型——总结(2)
内容总结:
我写的第一篇博客是梳理的logistic回归模型的原理,主要内容是总结Logistic回归模型实现二分类的整体流程。
这一篇是第二篇,总结一下怎么用numpy实现Logistic回归模型,numpy是python的一个数学运算的包(numpy深度的内容我还不知道,现在对他的理解就是:他的内容就是大学《线性代数》里面的知识)。
接下来就总结一下从理论到实战的过程。
这个实战过程也是《飞桨PaddlePaddle深度学习实战》这本书里面的内容,我写的是自己看完后的理解和总结,不是copy人家的哈哈哈!
问题:通过Logistic回归模型识别猫
1数据集X
1.1数据集X——数据整理
”万里长征第一步“就是准备数据,只有数据和数学公式是已知量,第一步就是准备数据集X
数据集是图片
图片的大小:64px*64px (像素)
图片类型:jpg,是rgb三个通道的jpg格式的图片
总结一下图片的知识:
玩ps的人应该很好理解(不玩的也容易理解),和led屏差不多一个原理,这些数据集的图片都是64x64的像素点组成的一个矩阵,就像下面的这个图片,图片文件可以认为是一个64行64列的3个矩阵,每个空格里面就是放着一个像素点,这个像素点的大小是0-255(应该是一个字节的大小,2^8),这三个矩阵就是这个图片的全部信息。
图片的知识总结到此为止!

-————————————————————————————
现在知道图片是用矩阵表示的了,现在就要把这个信息转换成上一篇中数据形式一样的数据才能计算。
上一篇中用到的样本信息是:
一条样本信息
[ x 1 x 2 x 3 . . . . . . x n ] \begin{bmatrix} x_1&x_2&x_3&......&x_n\end{bmatrix} [x1x2x3......xn]
一条标签信息
[ y 1 ] \begin{bmatrix} y_1\end{bmatrix} [y1]
总结:一条样本信息里面有n个变量,对应这一个标签信息里面的一个结果。
现在就要把这个图片的三个矩阵转换成一个”一行n列“的矩阵。
那么数据集的图片有几列呢?
n=64643
n=12288
这个数据很大,有1万多个变量对结果影响,说明也存在12288个权重w值。
另外:
数据集是百度提供的开源实验数据集,也提供一个名为utils.py的模块来加载数据集,这次也不用自己处理jpg格式的图片了,直接用百度提供的就可以。具体处理图片的方法改天再总结。
猫的图片数据集以hdf5文件的形式存储,包含了下面的内容:
1.训练数据集 train_set
2.测试数据集 test_set
单个图片的数据存储形式为(px_num,px_num,3),px是像素的意思,px_num表示图片的长度或宽度,都是64个像素,数字3表示3个通道rgb。
import h5py
import numpy as np
def load_data_sets():
"""
用于从两个.h5文件中分别加载训练数据和测试数据
Args:
Return:
train_x_ori: 原始训练数据集
train_y: 原始训练数据标签
test_x_ori: 原始测试数据集
test_y: 原始测试数据标签
classes(cat/non-cat): 分类list
"""
train_data = h5py.File('data/data38223/train.h5', "r")
# train set features
train_x_ori = np.array(train_data["train_set_x"][:])
# train set labels
train_y_ori = np.array(train_data["train_set_y"][:])
test_data = h5py.File('data/data38223/test.h5', "r")
# test set features
test_x_ori = np.array(test_data["test_set_x"][:])
# test set labels
test_y_ori = np.array(test_data["test_set_y"][:])
# the list of classes
classes = np.array(test_data["list_classes"][:])
train_y_ori = train_y_ori.reshape((1, train_y_ori.shape[0]))
test_y_ori = test_y_ori.reshape((1, test_y_ori.shape[0]))
result = [train_x_ori, train_y_ori, test_x_ori,
test_y_ori, classes]
return result
这里先插入一下utils的代码,方便查看。这个模块里面有一个方法load_data_sets(),注释里面可以先了解到,这个方法的传入参数Args为空,不需要传入值,我们建立工程的时候需要按照这里的文件夹名称放进去相应的文件就可以。
Returen返回的值有5个,分别为train_x_ori:原始训练数据集
train_y:原始训练数据标签
test_x_ori:原始测试数据集
text_y:原始测试数据集标签
classes(cat/non-cat):分类list
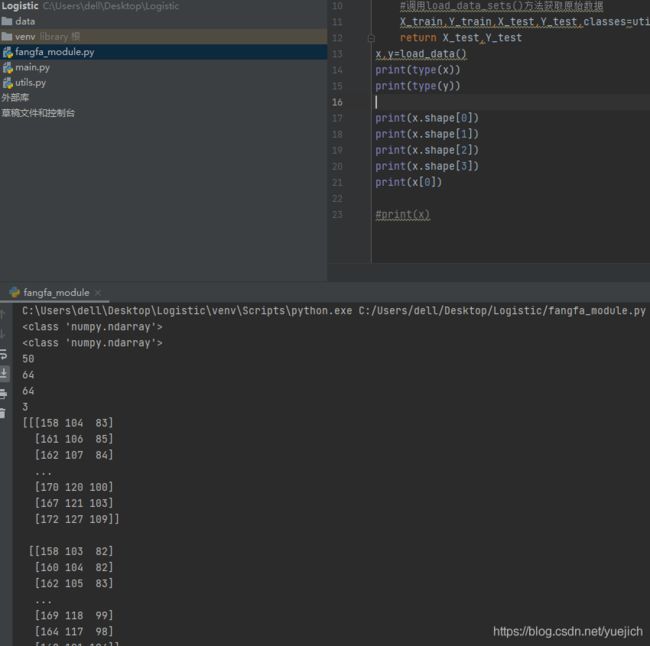
看一下hdf5的数据格式,上面的图片是看了一下X_test数据,总共是50条数据,这个1个ndarray矩阵式四维的,50个三维50个三维的 64行x64列x3个高的矩阵。
得到原始数据以后需要把这个数据格式转换成12288行1列的一维矩阵
代码:
#定义一个变量等于矩阵的列数
data_dim=px_num*px_num*3#也就是12288
X_train=X_train.reshape(train_num,data_dim).T#这个代码就是把这个数据变换成一个train_num行,data_dim列的一个二维矩阵,然后转置
看一下上面的这个图,这样x就变成了50行,data_dim列的一个矩阵(因为测试集里面只有50张图片)
那现在要把这个x转置一下,就是
X=X.T
目的是把他变成一个data_dim行50列的一个矩阵,这样操作每组数据的排列顺序没有变换,相当于把这个矩阵翻了90度,
看运行效果

这张图片里面的每一列就是一个图片的详细信息,总共50列。
到这里基本把数据整理完毕。
1.2数据集X——数据归一
关于数据归一我不是很理解他的物理意义,但是数据归一这个操作很简单,也是矩阵的运算。
每个数据的大小是0-255范围内的一个数字,数据归一就是把这些数据全部映射到0-1以内。那就把这个矩阵的每个变量全部除以255,因为数据需要float类型的,所以,用代码表示就是:
X=X/255.#在255后面加了一个点,这样就是float类型,
在这里我强调一下,这整个过程中用的x的类型其实是numpy里面的adarray,所有的这些方法包括reshape .T,还有这里的除以255,都是用的adarray这个类型的方法。
上面这个代码运行一下截图:
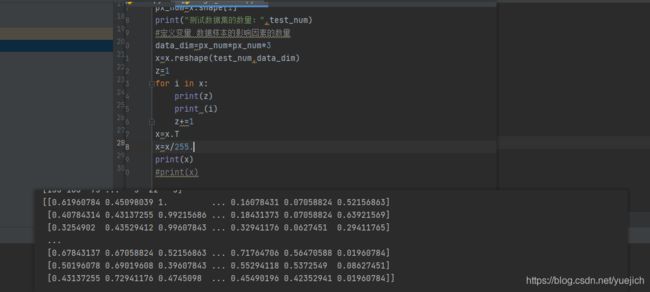
看下这个运行结果是不是都在1以内了。
————————————————————————————————
2.这一步先创建第一层网络里面的非线性变换
sigmoid()函数,映射预测结果到0和1
def sigmoid(x)
"""
args:x
return:
"""
return 1/(1+np.exp(-x))
2.1怎么产生sigmoid()函数的传入参数x
看到sigmoid()需要传入一个参数,这个参数就是结果的预测值,现在数据有了,没有权重,下面就要先猜一个权重,初始化一下这些参数
3.初始化模型参数
定义一个初始化函数 initialize_parametera
def initialize_parametera(data_dim)
"""
args:需要传入一个数值
这里初始化的是权重向量w和b,权重w有多少个呢?
有64x64x3
"""
#初始化w为一个(data_dim,1)的0向量,data_dim表示w参数的个数。
W=np.zero((data_dim,1),dtype=np.float)
b=0
return W,b
这个也很简单,也能理解了,但是不好理解什么是零向量,这都是数学概念,下面看看什么是零向量
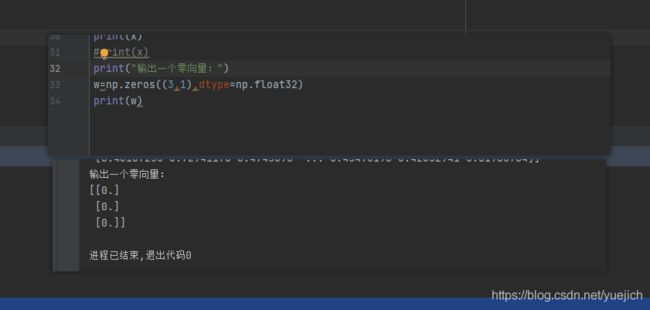
这是运行了一个代码的图片,三行1列,每一个参数都是一个0.
总结:到此为止,W,b的参数也有了,

还记得这张图片吗?这张图片的x数据每一列是一张图片,这个w呢,也是一列,所以现在就可以求sigmoid()函数里面的传入值y预测了
y y y= W W W. T T TX X X X+b
这里为什么w要转置应该就明白了吧,把w转换成横向的向量,在乘x加上b就算出了y的预测值,这个值return给sigmoid()函数就可以了
到这里 w,b ,y预测,y值,x值,都有了,下面就是定义损失和成本函数了,然后对成本函数求偏导。
这一篇先写道这里,明天再写一篇吧,不知不觉中写了5000字了,加油!