【2021 MCM】 Problem A: Fungi by 2100454

【2021 MCM】 Problem A: Fungi by 2100454

这里是历年美赛论文解读，那就从这里开始叭！！！

这次是2021年美赛A题，来自队伍2100454的O奖论文：
 
GAME：基于Gause模型的真菌生存策略和生物多样性研究

一、题目分析

1.1 问题总述

1. 题目首先从一篇文章的观点：

生长缓慢的真菌菌株在湿度和温度环境变化的情况下往往能够更好地生存和生长，而生长较快的菌株往往对相同的变化不太适应。

开始引入，提出了生长速度对真菌适应环境的影响的观点。

2. 接着，题目提出了核心任务:

这些研究人员检查了与不同真菌相关的大量性状，以及它们在分解地面凋落物（枯死植物材料）和木质纤维中的作用。对于这个MCM问题，你应该关注真菌的两个特性：真菌的生长速度和真菌对水分的耐受性。您的主要目标是模拟给定地块中木质纤维的分解，并在同一区域存在多种真菌分解木质纤维的情况下进行.

这里有几个关键词：

真菌、分解凋落物和木制纤维、生长速度和水分耐受性、模拟分解、同一区域多种真菌

可以看出，题目主要是要求你研究真菌的生长和真菌分解物质。

3. 接着，题目抛出了一系列问题：

• 使用 (生长速率和耐湿性)与分解速率 两个特性，不同的真菌如何在不同的环境中相互作用并分解固定地块中的地面垃圾？
• 在这些不同的环境中，随着条件的变化，分解会受到怎样的影响？
• 环境变化和环境变化的变化如何影响分解的长期动态，以及给定环境中真菌之间的竞争？

这里多了几个关键词：

不同环境真菌的相互作用、环境变化对分解的长期影响、真菌间的竞争

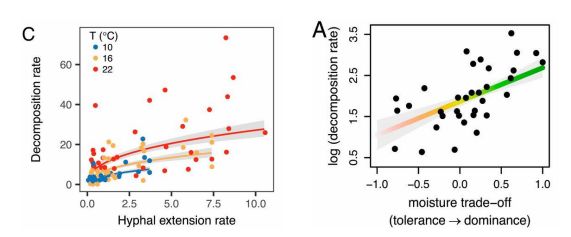
4. 然后，题目给出了两幅图，分别是生长速率和分解速率的关系，耐湿性和分解速率的关系

我们可以大致地看出它们都是正相关的。

其中图一分析了不同的温度条件，以真菌的菌丝延伸率代表生长速率。

两幅图的研究时间都是122天。

5. 总的来说，文章总述中我们可以看出以下重点：

建模着重需要关注“外部条件（湿度、群落间竞争）和内在性状（生长速度、耐湿性）是如何影响真菌对木质纤维、枯枝落叶的分解速率。”

1.2 具体任务

任务一：建立一个数学模型，描述在多种真菌存在的情况下，通过真菌活动分解地面凋落物和木质纤维。

关键词：多种真菌、活动分解

我的想法：

• 第一问一般都会比较简单，应该建立简单的线性模型就ok了。
  $$\begin{array}{rl}f(\mathbf{x};\mathbf{w})& =w_1{x}_1+w_2{x}_2+\cdots +w_D{x}_D+b\\ & ={\mathbf{w}}^{\top }\mathbf{x}+b\end{array}$$
• $x_1、x_2、x_3\dots \dots$可以为环境湿度生长速度、耐湿性等
• $f(\mathbf{x};\mathbf{w})$ 主要描述的是分解效果，可以抽象为分解物的质量、体积、密度变化等

任务二：在您的模型中，结合不同种类真菌之间的相互作用，它们具有不同的生长速率和不同的耐湿性。

关键词：结合不同种类真菌之间的相互作用

我的想法：

• 初一看，第二个任务和第一个任务好像，有点不知道从哪里开始下手。
• 然后，我觉得主要是要抓住结合不同种类真菌之间的相互作用这一点，在线性模型种加入不同真菌之间相互作用这一自变量。
• 这个不同真菌之间相互作用可以是两种真菌之间的，也可以是多个种类之间的，要把不同情况产生的影响列出来，与第一个任务种的模型进行对比。

任务三：提供模型分析并描述不同类型真菌之间的相互作用。应描述相互作用的动态，包括短期和长期趋势。你的分析应该检查对环境快速波动的敏感性，你应该确定不断变化的大气趋势的总体影响，以评估当地天气模式变化的影响。

关键词：相互作用、短期和长期趋势、对环境快速波动的敏感性、大气趋势对天气模式的影响

我的想法：

• 任务三更加关注不同时间的影响，要结合长期和短期进行分析。
• 加入一些环境快速变化的因变量
• 同时要多找一些大气和天气的资料

任务四： 包括对每种物种和可能持续存在的物种组合的相对优势和劣势的预测，并对不同环境进行预测，包括干旱、半干旱、温带、树栖和热带雨林。

关键词： 组合、优势和劣势、不同的环境

我的想法：

• 用不同的组合进行对比
• 建立预测模型
• 结合真实情况的不同环境

任务五：描述一个系统中真菌群落的多样性如何影响系统在地面垃圾分解方面的整体效率。预测生物多样性在当地环境存在不同程度变化的情况下的重要性和作用。

关键词： 多样性、整体效率

我的想法：

• 对比于前面的题目，最后一个任务更关注的是真菌多样性对环境的影响，但前面主要是环境对真菌的影响
• 需要建立预测模型

其实读完了所有任务，我的脑海中只有建立简单的线性模型和预测模型的想法，可能是因为知识储备还不够，那就读一下优秀论文学习一下叭。

1.3 需要提交的内容

提交一份不超过25页的PDF文件，包括：
 

• 一页总述
• 目录
• 完整的解决方案
• 两页结果文章
• 参考文献列表

二、论文解读

2.1 摘要

摘要的第一段复述了题目中是一些关键信息，并总述了自己要完成的任务。

真菌对有机物的分解是碳循环不可或缺的一部分，可以使碳在环境中重复利用。最近的一篇文章探讨了不同性状对其分解效率的影响。在本文中，我们关注两个主要特征，菌丝延伸率和耐湿性，以及真菌之间的相互作用和各种环境条件，以模拟木质纤维的分解，并理解生物多样性的重要性。

---

摘要的第二段介绍了GAME模型的来由：由任务的四个首字母组成。

并讲述自己建立了一个预测模型来模拟，主要的模型方法为一个高斯竞争模型，并采用微分方程的形式进行推导。

因此，摘要的第二段用来总体介绍自己的模型。

---

其次，作者用Firstly，Secondly，Thirdly，Fouthly清晰地列出自己完成任务的每一点。

在Firstly中，简述了自己预测前的一些假定，并给出预测的结果，并和已知结果对比证明自己预测的正确性，对应了任务一和任务二。

在Secondly中，简述了自己选择的五种具有代表性的真菌，并给出了长期和短期和在环境快速波动情况下的生长情况，对应任务三。

在Thirdly中，介绍了选用五个温度带的不同城市进行分析，并给出了分析的结果和进一步推断的结论，对应了任务四。

在Fourthly中，介绍了改变真菌数量来研究生物多样性对环境的影响，并给出了正相关的结论，对应了任务五。

---

最后一段写了After modeling，进行了灵敏度分析，并总结了优势和劣势，最终给出了结论。

---

关键词：分解速率，多环境，高斯模型，生物多样性

关键词主要来自于分析的任务和建立的模型

---

因此，通过阅读摘要，我发现它主要做了以下几个工作：

1. 复述文章关键信息，总述完成自己的任务。
2. 总体介绍自己的模型。
3. 利用分点的形式，介绍了自己对应每个任务进行的工作，以及得出的结论。
4. 陈述自己完成建模后的工作：灵敏度分析、优势劣势、总结。
5. 关键词总结。

2.2 目录

• 目录由大标题、日期、Contens、各级标题组成
• 只有{section}的字体是加粗的，且后面没有页码连接符
• 标题一共有三级，每级都会有缩进

2.3 简介

• Introduction 由 Background 和 Our work 和 Data Pre-processing 三部分组成。

Background

• Background中的对题目的背景进行介绍，并配上了一幅图来更加清晰直观地描述背景。

我们的工作

1. 第一段是总起，引出下面五个任务的分析。
2. 接下来有四段，分别描述了四个任务。
3. 每一段分两个部分，第一部分用 Task_i+斜体 简要地概括自己完成的任务，格式为用的模型类型（预测模型，分类模型）+完成了什么任务。
4. 第二部分用正体字更加详细地描述了用了什么数据+具体的模型是什么+模型建立的一些指标。
5. 接下来画了一个流程图来描述和总结上面提到的任务。

数据预处理

• 这一部分主要用来描述数据预处理

• 因为题目给的数据不是线性的，所以作者给数据取了一个log值，并使用最小二乘法，以更好进行线性回归分析，并将处理好的数据画图。

• 然后将数据总结到一个三线表，描述了每组数据的斜率、截距、方差、P值

2.4 假设

为了简化问题，作者做了以下的假设：

接着作者列出了五点假设，每点都有Assumption和justification

• 采用中期的分解速率
• 生长速率与菌丝延伸率成正相关
• 所有菌丝都具有相同的环境容量
• 外部菌丝的扩散可以忽略
• 没有人类活动的影响

建模中的假设要符合以下要求：

1. 针对问题的主要因素，忽略次要因素，排除一些小概率事件

2. 使我们要解决的问题简化，使模型更合理化；

2.5 缩写和定义

这里主要写一些公式和符号的缩写和定义

用一个三线表呈现，第一列是符号，第二列是定义，第三列是单位

2.6 The GAME Model

这一部分主要描述他们建立的模型的细节

2.6.1 Gause’s Model for Predicting Fungus’ Decomposition of Woody Fibers

在这一节，作者提出并介绍了高斯竞争模型和有限差分法。

• 高斯竞争模型来自于高斯提出的竞争排斥原理：由于竞争的排斥作用，生态位相似的两种生物不能在同一地方永久共存；
• 有限差分法是一种求解微分方程数值解的近似方法，其主要原理是对微分方程中的微分项进行直接差分近似，从而将微分方程转化为代数方程组求解。

作者列出了三条微分函数方程：

$$\{\begin{array}{l}\frac{dV}{dt}=-{\sum }_{i=1}^{s}f\left(T,\varphi ,\frac{d{l}_i}{dt}\right)\cdot V\cdot \left(1-\frac{F_1+F_2+\cdots +F_s}{K}\right)\\ \\ \frac{d{F}_i}{dt}=r_i(T,\varphi )\cdot F_i\cdot \left(1-c_{i1}(T,\varphi )\frac{F_1}{n_1}-c_{i2}(T,\varphi )\frac{F_2}{n_2}-\cdots -c_{is}(T,\varphi )\frac{F_s}{n_s}\right),i=1,2,\cdots ,s\\ \\ \frac{d{l}_i}{dt}=m_i(T,\varphi )\left(1-\frac{F_1+F_2+\cdots +F_s}{K}\right),i=1,2,\cdots ,s\end{array}$$

• 第一条公式表示了木质纤维相对密度随时间的变化
• 第二条公式表示了真菌密度随时间的变化
• 第三条公式表示了真菌长度随时间的变化

• $f（\cdot ，\cdot ，\cdot ）$：分解速率函数。
• $K$：真菌的综合环境容量。
• $r_i（\cdot ，\cdot ）$：与温度和湿度相关的每个物种的固有生长速率。
• $n_i$：每种真菌的环境容量。
• $m_i（\cdot ，\cdot ）$：与温度和湿度相关的每个物种的固有菌丝延伸率。
• $c_{ij}（\cdot ，\cdot ）$：物种i的相对竞争力。
• $c_i(T,\varphi )=1-\frac{m_i(T,\varphi )}{{\sum }_{j=1}^s{m}_j(T,\varphi )}$

这里列出的公式和黄皮书上的物种竞争模型部分类似

• 有了上面的公式，接下来就是要想怎么代入数值进行计算了。而且我们观察上面三条公式可以发现，第二条公式是第一条公式和第三条公式的基础，所以要先解第二条公式。因此，作者就创造了三种不同品种的真菌，有不同的生长率、延伸率、消耗率。
• 然后可以代入数值用matlab解方程，并画出线图，并分析图中的结果。
• 最后解第一条公式和第三条公式，也画出线图，也分析图中的结果。

2.6.2 Antagonism Effect and Stability

在这一部分中，作者选择了温带环境作为实验环境，分析了大气变化趋势对真菌生长模式的影响，并评估了当地气候模式的变化对木质纤维分解速率的影响。

作者挑选了五种真实存在的不同的菌种进行实验。

1. 低水势高延伸率
2. 忍受恶劣环境的低延伸率
3. 只适应高水势
4. 适应高温，延伸率最大
5. 潮湿低温

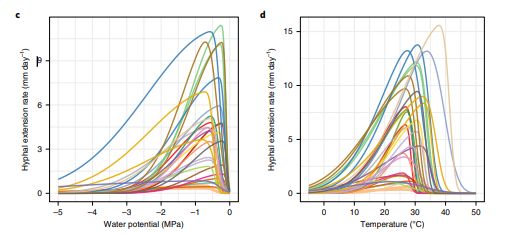
然后将这五种菌种的数据分别以温度和湿度为自变量，菌丝延伸率为因变量画出了两幅线图。

作者找的资料来源于这篇文章
Consistent trade-offs in fungal trait expression across broad spatial scales
画的图也是参考了文章中下面这幅图
 

然后绘制了五幅雷达图来描述五种菌种的五个特性：耐热性、耐热性、耐湿性、真菌在最佳温度下的分解速率、真菌在最佳湿度下的分解速率

接着，作者从气候网站 Weatherunderground 上面收集了俄亥俄州哥伦布市短期（168h）和长期（122天）的温度和湿度的数据

作者引入了一个新的变量耐湿系数 $G(\varphi )=\frac{{\mu }_1^i(\varphi )}{{\mu }_1^i\left({\varphi }_0\right)}$，即在某一湿度下的延伸率比最大延伸率，并将耐湿系数>=50%的区间成为一个最佳水分区间的标准，分析根据区间的大小分析菌丝的耐湿性。接着把湿度指标换成温度，做同样的分析。

接着作者采用插值和对数几率回归的方法作出了在不同温度下菌丝延伸率和木质分解率的关系图

接着，作者将菌丝延伸率定义为$m_i(T,\varphi )=m_{\max }^i\cdot G(\varphi )\cdot H(T)$，即（最大菌丝延伸率 * 耐湿系数 * 耐温系数，并用 $r_i=p\cdot m_i$ 描述菌丝生长率和菌丝延伸率的关系，并根据天气数据绘制出长期和短期内温度和湿度与菌丝密度的线图。

这里主要做的工作是，把温度、湿度、时间数据结合起来，一起分析它们对菌丝密度的影响。

2.6.3 Multi-environment Experiment for Revealing Habitats

在本节中，作者在干旱、半干旱、温带、树栖和热带雨林等不同环境中进行了与上一个任务类似的长期实验。

作者用一幅地图拼上每个地点的放大图、

然后画了五行图，每行为每个地点的温湿度图和时间和菌丝密度关系图

再画了两幅线图，对比了五个地点短期和长期的分解效率。

2.6.5 Efficiency, Robustness, and Biodiversity

这一节主要讲了生态系统的多样性

作者研究了五种真菌、三种真菌、两种真菌在热带的122天的分解效率，并画成了线图，得出以下结论：

$$\left[D_5^5,D_3^5,D_2^5\right]=[63.803\%,43.116\%,34.110\%]$$

可以看出分解效率随着真菌种类数量的减少而减少。

接着还分析了其它环境的情况，并做出了对比。

接着作者设计了不同地区之间多样性下降影响率的比较，公式为：

$$I^i=\frac{1}{3}\left[\frac{D_5^i-D_3^i}{D_5^i}+\frac{D_5^i-D_2^i}{D_5^i}+\frac{D_3^i-D_2^i}{D_3^i}\right]$$

并得出了以下结论:

干旱地区$I_1=18.405\%$，热带雨林地区$I_5=33.283\%$。 这说明在某种程度上，热带雨林比干旱地区需要更充足的生物多样性，

2.7 灵敏度分析

我们需要选择那些有较大不确定性的参数进行灵敏性分析，如果这些参数改变对模型的影响不大，说明这个模型的泛化能力强，是稳定的。

在这篇论文中，作者选用了菌丝的延伸率和环境的容量作为灵敏度分析的对象。

并通过一副热力图来直观地给出在这两个值变化时，分解率的变化情况，并给出论文选择的菌丝的延伸率和环境的容量附近模型是收敛的的（因变量的上升/下降率为0）的结论，证明了模型的稳健性。

2.8 模型的优点和缺点

优点：

• 普适性强。除了真菌外，还可以应用到其它生物。
• 可解释性强。符合常识且有文献支持。
• 精度高。对于波动的环境也能很好地预测。

缺点：

• 决策粗略。选用的温度指标是间断的，使用了插值的方法进行处理。
• 竞争指标选择单一。不同真菌的竞争力可能不一样。

2.9 总结

文章用了比较简短的一段话进行总结。

主要描述了使用的模型和完成的工作。

2.10 附上的两页文章

这篇文章是大学水平的生物入门教科书。，主要有以下四个部分：

• 真菌是什么？
• 真菌在生态系统中的角色。
• 介绍自己建立的高斯模型。
• 生物多样性的重要性。

2.11 参考文献

参考的文献主要来源于一些外网的官网。

2.12 附录

这里附上了两页的python核心代码、主要是一些numpy、pandas、matplotlib的操作

三、论文优缺点总结

优点

1. 论文画的图非常丰富，集合了线图，散点图，雷达图，热力图，地图，且几乎每一页都至少会有一幅图。
2. 文章很有创意性，将四个任务的首字母进行组合，形成一个独创的Game模型，模型有创意且有难度。
3. 文章的完成了所有的任务，且得出的结论符合要求。

缺点：

1. 有部分细节上的错误。
2. 思路某些地方有一点混乱。