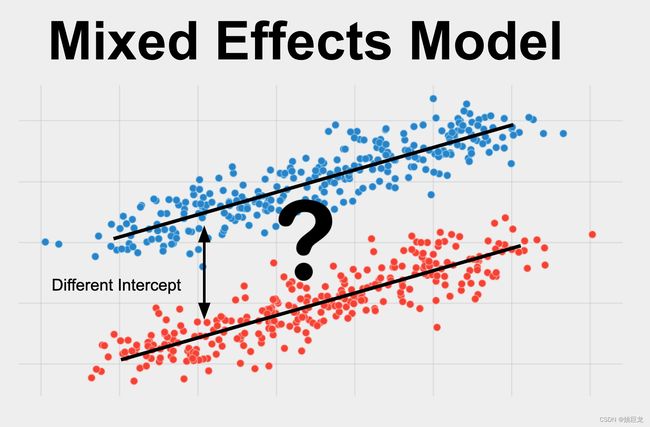
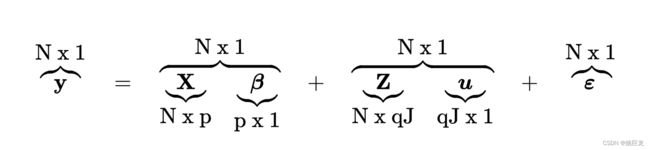线性混合模型（Linear Mixed Models）与R语言 lmer() 函数

---

社会理论告诉我们：人与人之间是有差异的，而且总是生活在一定的社会环境（social context）中，其表现和行为方式总是随着其置身于其中的社会环境的变化而变化。个体与社会环境之间的这种互动关系就决定了社会研究所用数据中的多层结构（multi-level structure）。

一般来讲，在同一个社会环境下的个体之间的异质性要小于不同社会环境下的个体之间的异质性。而这就违背了OLS回归技术的经典假定——误差项独立和同方差。

一、背景

线性混合模型（Linear Mixed Models） 是简单线性模型的扩展，允许固定效应和随机效应，特别适用于数据不独立的情况，例如来自分层结构的数据。

当数据有多个级别时，结果的变异性可以被认为是组内或组间的差异。例如患者级别的观察不是独立的，由同一位医生看病的患者更相似，在以更高级别的抽样单位，例如以医生为抽样单位时，同一医生的患者就可以认为是独立的。

如下图显示了一个样本总体，其中圆点表示患者，较大的圆圈代表同一医生的所有患者。

（1）处理分层数据的一种最简单的方法是聚合。

假设我们不是使用所有不独立个体患者的数据，而是从每个医生那里抽取 10 名患者，并取该医生内所有患者的平均值，从而汇总得到了独立的数据。那这样通过聚合数据分析就可以产生一致的效果估计和标准误差。

但是这种方法并没有真正地利用所有数据，在聚合级别上，我们其实只有六个数据点。

（2）另一种方法是一次分析一个单元的数据。

在上述示例中，我们可以运行六个单独的线性回归——即样本中的每一个医生一个线性回归。同样，尽管这确实有效，但产生的模型数量太多，并且每个模型都没有利用其他医生数据中的信息。

这可能使得结果“嘈杂”，因为每个模型的估计都没有基于足够数据。

二、线性混合模型

线性混合模型（Linear Mixed Models）（也称为多级模型）可以被认为是上述两种选择之间的权衡。

方法二中的个别线性回归有大量数据去做回归估计，但噪音很大；方法一中聚合得到的噪音较小，但可能会因为对每个医生内所有样本进行平均而失去重要差异。线性混合模型LMM 正是介于这两者之间，它除了纠正数据中非独立性的标准误差之外，还可以去探索组内和组间效应之间的差异。

如上图所示，在这里，我们再次对这些来自六位医生的患者做了回归，并且可以根据散点图来分析预测变量和结果之间关系：在每个医生中，预测变量和结果之间的关系是负相关的；然而，在医生之间，这种关系是正向的。LMM让我们能够探索和理解这些重要的因素。

（一）分析思路

由上述这个例子可以看到，线性混合模型的分析思路其实比较简单。它首先将多层结构数据在因变量上的总变异明确区分成组内（within-group）和组间（between-group）两个层次，然后分别在不同的层次上引入自变量来对组内变异和组间变异加以解释。

最简单的线性混合模型也不过如此，由一个组内方程和一个组间方程构成，同时将组内方程的部分或全部参数作为结果变量由组间方程来加以解释。患者为组内（即层1）分析单位，医生作为组间（即层2）分析单位。

（二）随机效应和固定效应

• 固定效应： 表示在观察中持续存在的总体水平效应。固定效应是不变的参数，模拟平均趋势。
• 随机效应： 是相关数据点的集群，模拟这些趋势在某些分组因素水平上变化的程度，以说明特定组合样本的行为可能与平均趋势不同。

线性混合模型的核心是“混合”。 因为它同时对固定效应和随机效应进行建模。

对于固定效应，我们可以假设总体中有一条真正的回归线，其参数为$\beta$，并且我们可以得到其估计 $\hat{\beta }$。

而随机效应是本身就是随机变量的参数。例如，我们可以说 $\beta$ 的分布为具有均值 $\mu$ 和标准差 $\sigma$ 的随机正态变量，或者以方程形式：
$$\beta \sim \mathcal{N}(\mu ,\sigma )$$

这实际上与线性回归相同，线性回归中我们假设数据是随机变量，参数是固定效应。而现在，数据是随机变量，参数是每个层级的随机变量，但在最高级别是固定的（例如，我们仍然假设一些总体平均数 $\mu$）。

三、模型理论

（一）名称表述：MA/HLM/MEM/GCM

线性混合模型名称繁多：

社会学研究者称其为多层线性模型（multilevel models）
教育学研究者将其称为分层线性模型（hierarchical linear models）
计量经济学者往往称其为随机系数回归模型（random-coefficient regression models）
统计学家则更多地称其为混合效应模型（mixed effect models）和随机效应模型（random-effects models）
发展心理学研究者多称其为增长曲线模型（growth-curve models）。

另外，多层线性模型有一个特例，被习惯称作协方差成分模型（covariance components models）。

（二）表达式

$$\mathbf{y}=\mathbf{X\beta }+\mathbf{Zu}+\mathbf{\epsilon }$$

• $\mathbf{y}$ is a $N\times 1$ column vector, the outcome variable;
• $\mathbf{X}$ is a $N\times p$ matrix of the $p$ predictor variables;
• $\mathbf{\beta }$ is a $p\times 1$ column vector of the fixed-effects regression coefficients (the $\beta$s);
• $\mathbf{Z}$ is the $N\times qJ$ design matrix for the $q$ random effects and $J$ groups;
• $\mathbf{u}$ is a $qJ\times 1$ vector of $q$ random effects (the random complement to the fixed $\mathbf{\beta }$ for $J$ groups;
• $\mathbf{\epsilon }$ is a $N\times 1$ column vector of the residuals, that part of $\mathbf{y}$ that is not explained by the model, $\mathbf{X\beta }+\mathbf{Zu}$.

展开如下：

（三）模型假设

混合效应建模的假设包括：

1. 线性度（Linearity）

我们研究的变量必须是线性相关的。这意味着，如果绘制变量，那么将绘制出一条适合数据形状的直线。

2. 无异常值（No Outliers）

研究的变量中不得包含异常值。线性回归对异常值数据点很敏感，我们可以通过绘制图像，并观察是否有任何点远离所有其他点来判断研究变量是否有异常值。

3. 范围内的类似分布（Similar Spread across Range）

即同方差性，它描述了变量何时在其范围内具有相似的分布。

4. 残差正态性（Normality of Residuals）

“残差”一词是指从实际值中减去预测值而得到的值。这些值的分布应符合正态（或钟形曲线）分布形状。

满足这一假设可确保回归结果同样适用于整个数据分布，并且预测中不存在系统偏差。

5. 无多重共线性（No Multicollinearity）

多重共线性是指两个或多个自变量相互之间具有显着相关性的情况。

当存在多重共线性时，回归系数和统计显着性变得不稳定且可信度降低，尽管它不会影响模型对数据本身的拟合程度。

四、示例

使用 lme4 附带的数据集 sleepstudy 在 R 软件中进行拟合。

（一）数据集说明

sleepstudy 数据集包含睡眠剥夺研究中受试者每天对精神运动警戒任务 (PVT)的平均反应时间（以毫秒为单位），每个受试者观察 10 天。感兴趣的是睡眠不足的受试者的反应时间如何随时间变化。

精神运动警戒任务( PVT ) 是一项持续注意、反应定时的任务，用于测量受试者对视觉刺激做出反应的一致性。研究表明，睡眠债务或睡眠不足的增加与警觉性下降、解决问题的速度变慢、精神运动技能下降和错误反应率增加有关。

Use of PVT tests was championed by David F. Dinges and popularized by its ease of scoring, simple metrics, and convergent validity.[1] However, it was shown that motivation can counteract the detrimental effects of sleep loss for up to 36 hours.

（二）数据可视化

首先，使用 data() 函数将数据集加载到全局环境中：

#install.packages("lme4")
library(lme4)
data("sleepstudy")

用 ggplot2 进行数据可视化：

library(ggplot2)
ggplot(sleepstudy) +
  aes(x = Days, y = Reaction) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE) +
  facet_wrap(~Subject)

可视化结果表明线性模型似乎是合适的。

但考虑到受试者之间的随机变化，似乎受试者对拟合线的截距和斜率产生了随机影响，因此我们可以拟合一个混合效应模型。

（三）使用 lmer() 函数拟合模型

1. (Days | Subject) syntax

为了将 Reaction 建模为具有以 Subject 为条件的截距和斜率系数的函数 Days，我们使用 lmer() 拟合以下模型：

m1 <- lmer(Reaction ~ Days + (Days | Subject), sleepstudy)

$(Days|Subject)$ ：表示我们要对截距的随机效应、Days 系数的随机效应以及随机效应之间的相关性进行建模。

随机效应是方差，因此我们可以用以下协方差矩阵对其进行符号化，其中 ${\sigma }_1^2$ 是截距随机效应，${\sigma }_2^2$ 是 Days 随机效应，${\beta }_{12}$ 是两个方差之间的相关性：
$$\left[\begin{array}{cc}{\sigma }_1^2& {\beta }_{12}\\ {\beta }_{12}& {\sigma }_2^2\end{array}\right]$$

通常协方差矩阵包含非对角线上的协方差，而不是相关性。 但我们以这种方式呈现它是为了符合 lme4 如何总结随机效应。 另外，相关性只是协方差的无单位版本。

summary(m1, corr = FALSE)

lme4 模型的汇总输出在“随机效应”下列出了估计的方差/标准差和相关性。
（summary() 函数中的 corr = FALSE 参数表示不显示固定效应的相关性）

> summary(m1, corr = FALSE)
Linear mixed model fit by REML. t-tests use
  Satterthwaite's method [lmerModLmerTest]
Formula: Reaction ~ Days + (Days | Subject)
   Data: sleepstudy

REML criterion at convergence: 1743.6

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.9536 -0.4634  0.0231  0.4634  5.1793 

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 Subject  (Intercept) 612.10   24.741       
          Days         35.07    5.922   0.07
 Residual             654.94   25.592       
Number of obs: 180, groups:  Subject, 18

Fixed effects:
            Estimate Std. Error      df t value Pr(>|t|)
(Intercept)  251.405      6.825  17.000  36.838  < 2e-16
Days          10.467      1.546  17.000   6.771 3.26e-06
               
(Intercept) ***
Days        ***
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

因此，随机效应的估计协方差矩阵（与非对角线相关）为：
$$\left[\begin{array}{cc}612.10& 0.07\\ 0.07& 35.07\end{array}\right]$$

2. (Days || Subject) syntax

对于上述协方差矩阵，我们可以将方差和相关性用数字标记，以指示它们在协方差矩阵中的位置：
$$\left[\begin{array}{cc}Var(1)& Corr(2,1)\\ Corr(2,1)& Var(2)\end{array}\right]$$

由于随机效应之间的估计相关性很小，约为 0.07，我们可以假设相关性为 0 并拟合一个更简单的模型。

这意味着对随机效应的协方差矩阵施加一些结构，如下所示：
$$\left[\begin{array}{cc}Var(1)& 0\\ 0& Var(2)\end{array}\right]$$

要使用 lmer() 指定这一点，我们在指定随机效果时使用两个pipes而不是一个：

# Notice the || in the random effects syntax
m2 <- lmer(Reaction ~ Days + (Days || Subject), sleepstudy)
summary(m2, corr = FALSE)

> summary(m2, corr = FALSE)
Linear mixed model fit by REML. t-tests use
  Satterthwaite's method [lmerModLmerTest]
Formula: Reaction ~ Days + (Days || Subject)
   Data: sleepstudy

REML criterion at convergence: 1743.7

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.9626 -0.4625  0.0204  0.4653  5.1860 

Random effects:
 Groups    Name        Variance Std.Dev.
 Subject   (Intercept) 627.57   25.051  
 Subject.1 Days         35.86    5.988  
 Residual              653.58   25.565  
Number of obs: 180, groups:  Subject, 18

Fixed effects:
            Estimate Std. Error      df t value Pr(>|t|)
(Intercept)  251.405      6.885  18.156  36.513  < 2e-16
Days          10.467      1.560  18.156   6.712 2.59e-06
               
(Intercept) ***
Days        ***
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

此时，“随机效应”部分没有估计相关性，是因为我们将它限制为 0。

（四）使用 lme() 函数拟合模型

对随机效应协方差矩阵的进一步约束是假设两个方差相等：
$$\left[\begin{array}{cc}Var& 0\\ 0& Var\end{array}\right]$$

在这种情况下，只有一个方差参数需要估计。根据我们迄今为止看到的估计随机效应，这是一个牵强的假设。第 0 天的受试者反应时间（截距）之间的变异性远大于他们估计的斜率之间的变异性。

lme4 包中的 lmer() 函数没有为这种类型的结构提供便利。为了使用这个模型，转向 nlme 包和函数 lme()，使用 random 参数。为了指定两种随机效应估计一个共同的方差参数，使用 pdIdent() 函数。

设置 Subject = pdIdent(~ Days) 并嵌套在一个列表中。

# no need to install, comes with R
library(nlme)
m3 <- lme(Reaction ~ Days, random = list(Subject = pdIdent(~ Days)), 
          data = sleepstudy)
summary(m3)

摘要输出显示截距和天数随机效应的标准偏差（方差的平方根）的一个估计值：8.89。

> summary(m3)
Linear mixed-effects model fit by REML
  Data: sleepstudy 
      AIC      BIC    logLik
  1767.15 1779.877 -879.5749

Random effects:
 Formula: ~Days | Subject
 Structure: Multiple of an Identity
        (Intercept)     Days Residual
StdDev:    8.898743 8.898743 27.37447

Fixed effects:  Reaction ~ Days 
                Value Std.Error  DF  t-value p-value
(Intercept) 251.40510  4.333705 161 58.01158       0
Days         10.46729  2.214483 161  4.72674       0
 Correlation: 
     (Intr)
Days -0.237

Standardized Within-Group Residuals:
        Min          Q1         Med          Q3         Max 
-3.77675971 -0.54676522  0.03842765  0.57370461  4.86391328 

Number of Observations: 180
Number of Groups: 18

参考资料

Silk MJ, Harrison XA, Hodgson DJ. 2020. Perils and pitfalls of mixed-effects regression models in biology. PeerJ 8:e9522 https://doi.org/10.7717/peerj.9522

Dinges, D. I, & Powell, J. W. (1985). Microcomputer analysis of performance on a portable, simple visual RT task sustained operations. Behavior Research Methods, Instrumentation, and Computers, 17, 652–655