旅行商问题 python 不同算法实现

货郎问题/旅行商问题(TSP)

一个网络上的最优路线问题，它寻求货郎走过网络上的所有点的路线最短。

定义：

• 输入 ： 有穷个城市的集合 $C=\{c_1,c_2,...,c_n\},距离d(c_i,c_j)=d(c_j,c_i)\in Z^{+},1\le i<j\le n$
• 解： $1,2,...,n$ 的排列 $k_1,k_2,...,k_n$ 使得： $min\{\sum _{i=1}^{n-1}d(c_{k_i},c_{k_{i+1}})+d(c_{k_n,c_{k_1}})\}$

问题描述：

​ 旅行商问题(Travelling Salesman Problem,TSP)又称为旅行推销员问题、货郎担问题，它是数学领域著名问题之一。假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是使求得的路径长度为所有路径长度为所有路径之中的最小值。

旅行商问题，即TSP问题，是数学领域中著名问题之一。

给定$n$个城市，每个城市之间存在一定的距离，具体而言，第$i$号城市到第$j$号城市的距离为$a_{ij}$。

1.采用蛮力法求TSP问题

1.1 蛮力法

一种简单直接地解决问题的方法，常常直接基于问题的描述，所以蛮力法也是最容易应用的方法。蛮力法所依赖的基本技术是遍历，也称扫描，即采用一定的策略依次理待求解问题的所有元素，从而找出问题的解。依次处理所有元素是蛮力法的关键，为了避免陷人重复试探，应保证处理过的元素不再被处理。

本题算法：求全排列算法

1.2代码实现

def dfs(position):
    global count, temp_dist, min_cost, min_index
    # 递归出口
    if position == len(arr):
        if temp[0] == start:
            count += 1
            temp.append(start)
            for i in range(3):
                temp_dist += distance[temp[i]][temp[i + 1]]
            temp_dist = temp_dist + distance[temp[3]][start]
            print(f"方案{count}为：", temp, f"路程为:{temp_dist}")
            if min_cost > temp_dist:
                min_cost = temp_dist
                min_index = count
            temp_dist = 0
            temp.pop()
        return
    # 递归主体
    for index in range(0, len(arr)):
        if not visit[index]:
            temp[position] = arr[index]
            visit[index] = True  # 试探
            dfs(position + 1)
            visit[index] = False  # 回溯。


if __name__ == "__main__":
    visit = [False, False, False, False]
    temp = ["" for x in range(0, 4)]
    count = 0 # 方案数
    temp_dist = 0 #临时路程
    min_cost = float("inf")
    min_index = None
    distance = [
        [0, 8, 5, 36],
        [6, 0, 8, 5],
        [8, 9, 0, 5],
        [7, 7, 8, 0]]  # 存储两个城市之间的距离
    arr = [0, 1, 2, 3]
    start = int(input("请输入开始结点："))
    dfs(0)
    print(f"最佳方案为：{min_index}，最优路程为：{min_cost}")

1.3 运行结果

1.4复杂度分析

当使用蛮力法解决TSP问题时，需要考虑从某个城市出发的所有路线。由于城市之间彼此互通，城市拓扑是个完全图，因此所有路线的数量规模是 $n-1$ 个城市的全排列。求1~n-1全排列的时间为$O(n\ast n!)$, 对于$O(n!)$ 的路径，求每条路径的长度的时间为 $O(n)$, 所以该算法的复杂度为 $O(n\ast n!)$。

2.采用动态规划求解TSP问题

3、 采用回溯法求解TSP问题

代码实现

4、 采用分枝限界法求解TSP问题

算法设计

解向量为$<1,i_1,i_2,...,i_{n-1}>$， 其中 $i_1,i_2,...,i_{n-1}$ 为 $\{2,3,...,n\}$ 的排列。

搜索空间为排列树， 结点$<1,i_1,i_2,...,i_k>$ 表示得到 $k$ 步路线。

约束条件： 令 $B=\{i_1,i_2,...,i_k\}$, 则 $i_{k+1}\in \{2,...,n\}-B$ 即每个结点只能访问一次。

代价函数与界

界：当前得到的最短巡回路线长度

代价函数： 设顶点 $c_i$ 出发的最短边长度为 $l_i$ ，$d_j$ 为选定巡回路线中第 $j$ 段的长度
$$L=\sum _{j=1}^k{d}_j+l_{i_k}+\sum _{i_j\notin B}{l}_{i_j}$$
其中 ： 为已走过路径长 ； 为剩余长度下界；

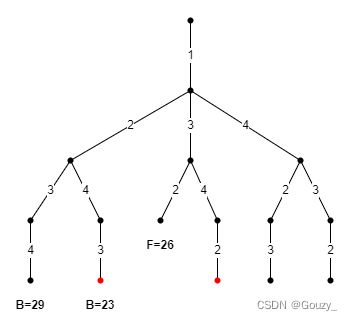
搜索树

过程分析：

• 第一个界： < 1, 2, 3, 4 >，长度为 29
• 第二个界： < 1, 2, 4, 3 >，长度为 23
• 结点 < 1, 3, 2 >: 代价函数值 26 > 23，不再搜索，返回 < 1, 3 >
• 结点 < 1, 3, 4 >, 代价函数值 9 + 7 + 2 + 2 = 20，继续，得到可行解 < 1, 3, 4, 2 > , 长度 23.
• 回溯到结点 < 1 >，沿着 < 1, 4 >向下…

最优解为 < 1, 2, 4, 3 > 或 < 1, 3, 4, 2 >，长度 23.

约束条件:只能选没有走过的结点代价函数:走过长度+后续长度的下界

时间复杂度:O(n!)

代码：

#include  
using namespace std;
#define MAX 1000  
int g[100][100], x[100], bestx[100];
 
int cl = 0, bestl = MAX, n;
 
//界定函数，按照屈婉玲老师的算法公开课视频讲解的给出的实现，这与网上绝大多数版本的界定函数不同，可以更精确的削减分支
double Bound(int t, int cl)
{
	double min1 = 0, min2 = 0, tempSum=0;
	for (int j = t; j <= n; j++)
	{
		if (g[x[t - 1]][x[j]] != -1 && g[x[t - 1]][x[j]] < min1)
		{
			min1 = g[x[t - 1]][x[j]];
		}
		for (int i = 1; i <= n; ++i)
		{
			if (g[x[j]][x[i]] != -1 && g[x[j]][x[i]] < min2)
			{
				min2 = g[x[j]][x[i]];
			}
		}
		tempSum += min2;
	}
 
	return cl + min1 + tempSum;
 
}
 
 
void Traveling(int t)
{
	int j;
	if (t>n) //到达叶子结点  
	{
		
		if (g[x[n]][1] != -1 && (cl + g[x[n]][1]> n;
	cout << "请输入城市之间的距离" << endl;
 
	for (i = 1; i <= n; i++)
		for (j = 1; j <= n; j++)
			cin >> g[i][j];
 
	for (i = 1; i <= n; i++)
	{
		x[i] = i;
		bestx[i] = 0;
	}
 
	Traveling(2);
	cout << "城市路线：" << endl;
	for (i = 1; i <= n; i++)
		cout << bestx[i] << ' ';
	cout << bestx[1];
	cout << endl;
	cout << "最短路线长度：" << endl;
	cout << bestl << endl;
	return 0;
}

5.采用贪心法求解TSP问题

5.1 分析

实际上TSP问题不满足贪心法的最优子结构性质,所以采用贪心法不一定得到最优解,但可以采用合理的贪心策略,如可以采用最近邻点策略,即从任意城市出发，每次在没有到过的城市中选择最近的一个,直到经过了所有的城市,最后回到出发城市。

5.2 代码实现

5.2 代码实现

5.3 时间复杂度

为$O(n^2)$

6.时间复杂度分析

• 搜索树的树叶个数：$O((n-1)!)$ ，每片树叶对应 1 条路径，每条路径有 n 个结点.
• 每个结点代价函数计算时间 $O(1)$，每条路径的计算时间为 $O(n)$
• 最坏情况下算法的时间 $O(n!)$ (蛮力算法)