计算机机器视觉原理之分类器1

系列文章目录

第一章 Python 机器学习入门之分类器

---

---

机器视觉是什么

机器视觉是人工智能正在快速发展的一个分支。简单说来，机器视觉就是用机器代替人眼来做测量和判断。机器视觉系统是通过机器视觉产品(即图像摄取装置，分CMOS和CCD两种)将被摄取目标转换成图像信号，传送给专用的图像处理系统，得到被摄目标的形态信息，根据像素分布和亮度、颜色等信息，转变成数字化信号;图像系统对这些信号进行各种运算来抽取目标的特征，进而根据判别的结果来控制现场的设备动作。。

---

一、机器视觉核心人物以及难点

机器视觉做的最核心的任务：

跨越“语义鸿沟”建立像素到语义的映射

难点

1.视角
我们可以从不同方向去观察图片，但是机器不行，如果从正面提取了特征，一旦从侧面或者其他视角，就不会识别出来
2.光照
光照的变化会引起图像颜色发生变化，对于机器来说，算法的抗干扰的能力能决定系统的性能
3.尺度
尺度是相对的概念，计算机无法预计真实世界的情况，应该考虑所有情况，比如离得远，离得近都因该考虑进来
4.遮挡
如何将遮挡下的事物识别出来

5.形变
不同形态的事物是否能识别出来，比如站着的动物，坐着的动物，猫的被成为液体动物，不同形态的猫能否被识别出来也是一大难点
6.背景杂波

7.类内形变
8.运动模糊
图片出现残影。产生的原因：在单位时间内物体动作过大导致运动模糊
9.类别繁多

二、图像识别的方法

1.硬编码

设置一个分类器

def classify_image ( image ):
#Do something magical here
return class_label

输入一张图像，返回一个标签
这是通过硬编码方式（用人的理解编码），不过这是一件很困难的事，难点太多，只适合变化单一的图形。

2.常用方法

1.数据构建
（1)有监督（标签）
（2）无监督
2.分类器设计与学习

图像表示：
希望输入的图像能被算法接受，使用像素表示或者从图像抽取特征（室内场景），或者局部特征表示（适合遮挡的图像）
分类模型：
对图像进行预测，都会输出预测值，包含：
近邻分类器
贝叶斯分类器
线性分类器
支撑向量机分类器
神经网络分类器
随机森林
Adaboost

损失函数：评估分类模型的好坏
优化算法：损失值太大时，调整参数使损失值下降
一阶方法·梯度下降
·随机梯度下降
·小批量随机梯度下降
二阶方法
牛顿法
. BFGS
. L-BFGS

训练过程：
数据集划分
数据预处理
数据增强
欠拟合与过拟合
减小算法复杂度
使用权重正则项
使用droputi正则化
超参数调整
模型集成

3.分类器决策

评价指标：
正确率(accuracy)=分对的样本数/全部样本数
错误率(error rate)= 1一正确率
TOP1：只看第一个标签是否预测对
TOP5：五个标签对一个就算正确

三.设计分类器

1.线性分类器

CIFAR10数据集·
包含50000张训练样本、10000张测试样本分为飞机、汽车、鸟、猫、鹿、狗、蛙、马、船、卡车十个类别图像为彩色图像，其大小为32*32

分类器类型设计
三种图像类型
1.Binaty二进制图像（非白即黑）

2.Gray Scale 灰度图像 （0到255） 一个像素由一个byte表示

3.Color彩色图像 有三个值（R,G,B）一个像素3个byte

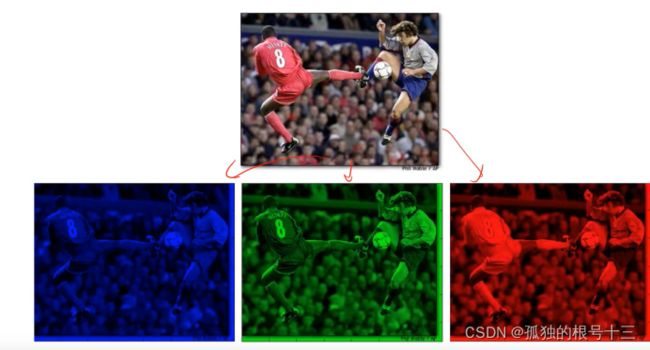
图像表示
大多数算法都要求输入向量

3072维=32×32×3
这个数据集是使用的彩色图形类型，一个像素3个byte

2.线性分类器具体定义

选择原因：形式简单、易于理解
通过层级结构(神经网络的基础)或者高维映射（支撑向量机)可以形成功能强大的非线性模型
定义：线性分类器是一种线性映射，将输入的图像特征映射为类别分数。

wi是3072维列向量，转置后与x点乘

即权重wi的转置与X点乘的结果相比较，分数最高的类别就识别成哪个类别

CIFAR10数据集分类任务的分类器，w，x，b的维度是多少?

CIFAR10有10个类别且图像大小为32x32x3，因此:
x_是图像向量，其维度为3072维;
W 是权值矩阵，其维度为10x3072
b是偏置向量，其维度为10x1的向量;
f是得分向量，其维度为10x1的向量
当x和模板很像时，得分就会变得很大，越大就越相似
权值看做是一种模板
输入图像与评估模板的匹配程度越高，分类器输出的分数就越高

从几何学看：分类器的任务：找到决策边界
决策边界：分数等于0的线就是决策面w转置x + bi = 0,i = 1,… ,c
w控制着线的方向
b控制着线的偏移
箭头方向代表分类器的正方向,沿着箭头方向距离决策面越远分数就越高。
如上图，这三条边就是决策边界，落在哪个里面哪个类型分数就高

四.损失函数

损失函数搭建了模型性能与模型参数之间的桥梁，指导模型参数优化。
损失函数是一个函数，用于度量给定分类器的预测值与真实值
的不一致程度，其输出通常是一个非负实值。
其输出的非负实值可以作为反馈信号来对分类器参数进行调整，
以降低当前示例对应的损失值，提升分类器的分类效果。
定义：
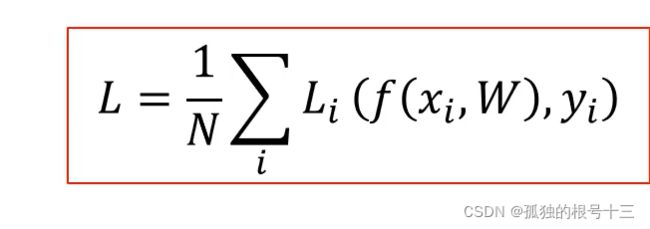x表示数据集中第i张图片;
f(xi,W)为分类器对xi的类别预测;
yi为样本i真实类别标签（整数);L;为第i个样本的损失当预测值;
L为数据集损失，它是数据集中所有样本损失的平均。

多类支撑向量机损失

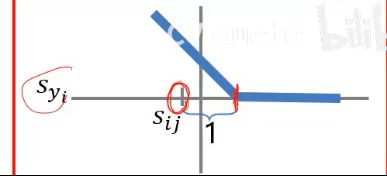
如果Syi正确类别的分数比其他分数加一分还高，损失就为0
其他类别分数加1比正确的高，损失就出现了，结果越大，损失就越大
sij =fj(Xj, wj,bj) = w xi + bj
j——类别标签，取值范围{1，2，…， c}
wj,bj——第j个类别分类器的参数;
xi ——表示数据集中的第i个样本
Sij–第i个样本第j类别的预测分数
Syi一第i个样本真实类别的预测分数
正确类别的得分比不正确类别的得分高出1分，就没有损失否则，就会产生损失

示例:假设有3个类别的训练样本各一张，分类器是线性分类器f(x,W)= Wx+b，其中权值W，b已知，分类器对三个样本的打分如下:


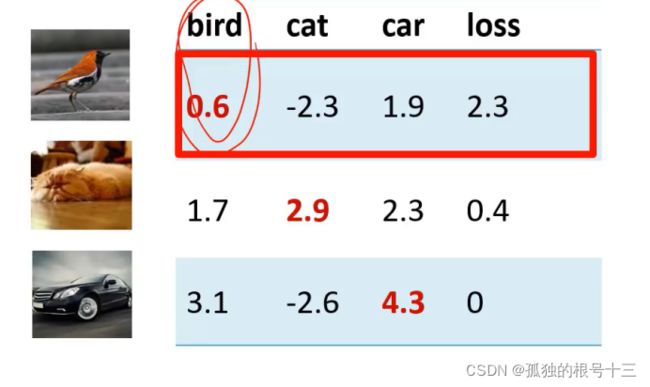
第二个图即使猫的权值最大，但是因为猫和车的分数相差没有超过一分，也会出现一定的损失，但是损失值比较小

将三个损失平均一下，此分类器损失为0.9

就是说Sij-Syi+1越小越好，代表没有损失，预测值减正确值加上1小于0就没有损失，预测正确。

参考资料

课程来自北京邮电大学计算机学院 鲁鹏老师
地址