原文:http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html
大多数人在高中,或者大学低年级,都上过一门课《线性代数》。这门课其实是教矩阵。

刚学的时候,还蛮简单的,矩阵加法就是相同位置的数字加一下。

矩阵减法也类似。
矩阵乘以一个常数,就是所有位置都乘以这个数。

但是,等到矩阵乘以矩阵的时候,一切就不一样了。
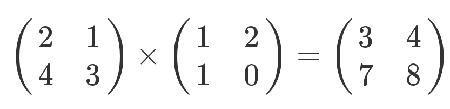
这个结果是怎么算出来的?
教科书告诉你,计算规则是,第一个矩阵第一行的每个数字(2和1),各自乘以第二个矩阵第一列对应位置的数字(1和1),然后将乘积相加( 2 x 1 + 1 x 1),得到结果矩阵左上角的那个值3。
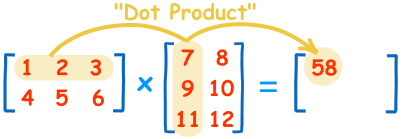
也就是说,结果矩阵第m行与第n列交叉位置的那个值,等于第一个矩阵第m行与第二个矩阵第n列,对应位置的每个值的乘积之和。
怎么会有这么奇怪的规则?
我一直没理解这个规则的含义,导致《线性代数》这门课就没学懂。研究生时发现,线性代数是向量计算的基础,很多重要的数学模型都要用到向量计算,所以我做不了复杂模型。这一直让我有点伤心。
前些日子,受到一篇文章的启发,我终于想通了,矩阵乘法到底是什么东西。关键就是一句话,矩阵的本质就是线性方程式,两者是一一对应关系。如果从线性方程式的角度,理解矩阵乘法就毫无难度。
下面是一组线性方程式。

矩阵的最初目的,只是为线性方程组提供一个简写形式。

老实说,从上面这种写法,已经能看出矩阵乘法的规则了:系数矩阵第一行的2和1,各自与 x 和 y 的乘积之和,等于3。不过,这不算严格的证明,只是线性方程式转为矩阵的书写规则。
下面才是严格的证明。有三组未知数 x、y 和 t,其中 x 和 y 的关系如下。

x 和 t 的关系如下。

有了这两组方程式,就可以求 y 和 t 的关系。从矩阵来看,很显然,只要把第二个矩阵代入第一个矩阵即可。

从方程式来看,也可以把第二个方程组代入第一个方程组。

上面的方程组可以整理成下面的形式。

最后那个矩阵等式,与前面的矩阵等式一对照,就会得到下面的关系。

矩阵乘法的计算规则,从而得到证明。
仿射变换
另外一篇博客http://blog.cocosdever.com/2016/03/11/Interpretation-of-the-relationship-between-CGAffineTransform-iOS-and-matrix/?utm_source=tuicool&utm_medium=referral
前言
今天接触了视图的2D变换,于是翻看了Apple Doc里面关于CGAffineTransform的用法.一开始我是直接阅读CGAffineTransformMakeScale部分,官方文档如下:
官方文档写得比较抽象加之陌生词汇较多,所以读了5分钟还是没搞清楚这个缩放和矩阵的关系(大学时候线性代数卷面分97,太久没用没灵感了),接着百度Google了一下发现大部分文章都是介绍怎么使用CGAffineTransform,并没有对CGAffineTransform本身的数据结构和矩阵关系结合起来,所以只能自己研究了,现在总结一下整个分析过程.关于仿射变换和CGAffineTransform的介绍这里不再描述.
- 生成需要变换的CGAffineTransform结构体
- 将CGAffineTransform赋值给view.transform属性(这一部通常定义成动画)
- 动画结束,将view.transform设置为CGAffineTransformIdentity,还原原样
一般来说,第1,2步应该是合并在一起的,类似
1
2
3
4
|
aView.transform =
CGAffineTransformMake(a,b,c,d,tx,ty);
aView.transform =
CGAffineTransformMakeScale(x, y);
|
设置动画方法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
[
UIView animateWithDuration:
0.3 animations:^{
aView.transform =
CGAffineTransformMakeScale(
2,
2);
} completion:^(
BOOL finished){
[
UIView animateWithDuration:
0.3 animations:^{
aView.transform =
CGAffineTransformIdentity;
}];
}];
[
UIView animateKeyframesWithDuration:
1.0 delay:
0.0 options:
0 animations:^{
[
UIView addKeyframeWithRelativeStartTime:
0 relativeDuration:
0.8 animations:^{
aView.transform =
CGAffineTransformMakeScale(
2,
2);
}];
[
UIView addKeyframeWithRelativeStartTime:
0.8 relativeDuration:
0.2 animations:^{
aView.transform =
CGAffineTransformIdentity;
}];
} completion:
nil];
|
动画结束后设置CGAffineTransformIdentity,其实就是把view.transform设置为默认值,如果放在动画里执行其实就相当于回播了一下动画.第三步非必须的.
上面我提前把CGAffineTransform的用法说了,目的是想让大家心里有底,知道CGAffineTransform的用法其实很简单,但是心里会产生一个疑问,就是CGAffineTransform和矩阵是什么关系?当然如果你心里没有这个疑问,那你百度一下缩放平移选择等基本用法就够了,也没必要往下看了
在CoreGraphics/CGAffineTransform.h头文件里面可以看到,CGAffineTransform的本质就是一个结构体,结构体长成这样
1
2
3
4
|
struct
CGAffineTransform {
CGFloat a, b, c, d;
CGFloat tx, ty;
};
|
从文档中可以看到CGAffineTransform代表一个3*3的矩阵 ,因为第三列固定是0 0 1,所以
CGAffineTransform结构体里面就只有6个元素了.此时你可能有疑问为什么第三列固定是0 0 1?下面会说到.
运算后view上的每一个点的x,y分别记为x’,y’计算公式为:
(其中x,y就是view做2D运算前的每一个点的座标,x’,y’就是2D变化后的view的每一个点的座标)
CGAffineTransform的本质就是一个结构体,而从CGAffineTransform的用法一节可以看到整个动画从头到尾无非就是在改变这个结构体的值,那么这个结构体的变化又和视图的变化怎么联系起来?这里个问题原本是从2D仿射变换的定义中推导出变换的公式,再从公式转为矩阵的设置的.这里我们就假设不懂2D仿射变换的公式吧,从程序中找到CGAffineTransform经过变换后的值,再与变换的公式对比,看看变换的值是否匹配矩阵,再理解变换和矩阵的关系.下面分别从视图的放大,缩小,平移,旋转分析.
放大和缩小
动画之前,先打印出view.transform的默认值
1
2
3
|
NSLog(
@"CGAffineTransformIdentity:%@",
NSStringFromCGAffineTransform(aView.transform));
|
将视图放大2倍之后,再打印出view.transform的值
1
2
3
4
|
aView.transform =
CGAffineTransformMakeScale(
2,
2);
NSLog(
@"Become bigger:%@",
NSStringFromCGAffineTransform(aView.transform));
|
如果你细心一点就会发现,其实CGAffineTransformMakeScale(x,y),设置的就是矩阵中的a和d.现在我们把经过放大2倍所生成的矩阵,按照CGAffineTransform的本质小节中的变换公式计算一下,看看能够得到什么结果
简单计算一下矩阵,可以得到
1
2
3
|
x' = 2x;
y' = 2y;
1 = 1;
|
好像发现了什么了~